 |
Схема выбора без возвращений
|
|
|
|
Элементы комбинаторики
Согласно классическому определению подсчет вероятности события А сводится к подсчету числа благоприятствующих ему исходов. Делают это обычно комбинаторными методами.
Комбинаторика - раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечного множества. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос «сколькими способами?».
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами умножения и сложения.
Правило умножения. Если из некоторого конечного множества первый объект (элемент х) можно выбрать n 1 способами и после каждого такого выбора второй объект (элемент у) можно выбрать n 2 способами, то оба объекта (х и у) в указанном порядке можно выбрать n 1∙ n 2 способами.
Этот правило распространяется на случай трех и более объектов.
Пример 2.1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если а) цифры не повторяются? б) цифры могут повторяться?
Решение:
а) Имеется 5 различных способов выбора первой цифры в числе. После того как первую цифру выбрали, осталось четыре цифры для выбора второй цифры числа. Для выбора третьей цифры числа остается три цифры. Следовательно, согласно правила умножения имеем  способов расстановки цифр, т.е искомое число трехзначных чисел - 60.
способов расстановки цифр, т.е искомое число трехзначных чисел - 60.
б) если цифры могут повторятся, то трехзначных чисел  .
.
Правило суммы. Если некоторый объект х можно выбрать n1 способами, а объект у можно выбрать n 2 способами, причем первые и вторые способы не пересекаются, то любой из указанных объектов (х или у), можно выбрать n 1 + n 2 способами.
|
|
|
Это правило распространяется на любое конечное число объектов.
Пример 2.2. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать для выполнения различных заданий двух студентов одного пола?
Решение:
По правилу умножения двух девушек можно выбрать 14∙13=182 способами, а двух юношей - 6∙5=30. Следует выбрать 2 студентов одного пола: 2 студенток или 2 юношей. Согласно правилу сложения таких способов будет 182+30 = 212.
Решение вероятностных задач часто облегчается, если использовать комбинаторные формулы. Каждая из них определяет число всевозможных исходов в некотором опыте, состоящем в выборе наудачу r элементов из n различных элементов рассматриваемого множества.
Существуют две схемы выбора r элементов (0< r ≤ n) из исходного множества: без возвращения (без повторений) и с возвращением (с повторениями). В первом случае выбранные элементы не возвращаются обратно; можно отобрать сразу все r элементов или отбирать их по одному. Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.
Схема выбора без возвращений
Пусть дано множество, состоящее из n различных элементов.
Размещением из n элементов по r элементов (0< r ≤ n) называется любое упорядоченное подмножество данного множества, содержащее r элементов.
Из определения вытекает, что размещения – это выборки, состоящие из r элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения. Число размещений из n элементов по r элементов обозначается символом  и вычисляется по формуле:
и вычисляется по формуле:
 , ,
| (2.1) |
или
 , ,
| (2.2) |
где  ,
,  ,
, 
Для составления размещения  надо выбрать r элементов из множества с n элементами и упорядочить их, т.е. заполнить r мест элементами множества. Первый элемент можно выбрать n способами, т.е. на первое место можно поместить любой из n элементов. После этого второй элемент можно выбрать из оставшихся n -1 элементов n -1 способами. Для выбора третьего элемента имеется n -2 способа, четвертого - n -3 способа, и наконец, для последнего r -го элемента - (n -(r -1)) способов. Таким образом, по правилу умножения, существует n (n -1)(n -2)... (n -(r -1)) способов выбора r элементов из данных n элементов, т.е.
надо выбрать r элементов из множества с n элементами и упорядочить их, т.е. заполнить r мест элементами множества. Первый элемент можно выбрать n способами, т.е. на первое место можно поместить любой из n элементов. После этого второй элемент можно выбрать из оставшихся n -1 элементов n -1 способами. Для выбора третьего элемента имеется n -2 способа, четвертого - n -3 способа, и наконец, для последнего r -го элемента - (n -(r -1)) способов. Таким образом, по правилу умножения, существует n (n -1)(n -2)... (n -(r -1)) способов выбора r элементов из данных n элементов, т.е.  .
.
|
|
|
Пример 2.3. Составить различные размещения по 2 элемента из множества  и подсчитать их число.
и подсчитать их число.
Решение:
Из трех элементов можно образовать следующие размещения по два элемента:
(a, b), (a, c), (b, a), (c, a), (b, c), (c, b).
Согласно формуле (2.2) их число
 .
.
Перестановкой из n элементов называется размещение из n элементов по n элементов.
Из определения вытекает, что перестановки – это выборки, состоящие из n элементов и отличающиеся друг от друга только порядком следования элементов. Число перестановок из n элементов обозначается символом Р n и вычисляется по формуле:
| Рn = n! | (2.3) |
Формула следует из определения перестановки:

| (2.4) |
Пример 2.4. Сколько различных перестановок можно составить из элементов множества  ?
?
Решение:
Из элементов данного множества можно составить следующие перестановки:
(2, 7, 8), (2, 8, 7), (7, 2, 8), (7, 8, 2), (8, 2, 7), (8, 7, 2).
По формуле (2.3) имеем
 .
.
Сочетанием из n элементов по r (0 ≤ r ≤ n) элементов называется любое подмножество, которое содержит r элементов данного множества.
Из определения вытекает, что сочетания – это выборки, каждая из которых состоит из r элементов, взятых из данных n элементов, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по r элементов обозначается символом 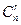 и вычисляется по формуле:
и вычисляется по формуле:
 . .
| (2.5) |
или
 . .
| (2.6) |
Число  размещений из n элементов по r элементов можно найти следующим образом: выбрать r элементов из множества, содержащего n элементов, затем в каждом из полученных сочетаний сделать все перестановки для упорядочивания подмножеств. Следовательно, согласно правилу умножения можно записать:
размещений из n элементов по r элементов можно найти следующим образом: выбрать r элементов из множества, содержащего n элементов, затем в каждом из полученных сочетаний сделать все перестановки для упорядочивания подмножеств. Следовательно, согласно правилу умножения можно записать:  , Отсюда
, Отсюда 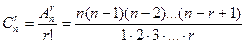 или
или 
 .
.
Можно показать, что имеют место формулы:
|
|
|
 , ( , ( ), ),
| (2.7) |
 , ,
| (2.8) |
 ( ( ). ).
| (2.9) |
Пример 2.5. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? Если выбрать 1 красную и 2 розовых гвоздики?
Решение:
Так как порядок выбора цветов не имеет значения, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно  способами. По формуле (2.6) находим, что
способами. По формуле (2.6) находим, что
 .
.
Красную гвоздику можно выбрать  способами. Выбрать две розовые из четырех имеющихся можно
способами. Выбрать две розовые из четырех имеющихся можно  способами. По правилу произведения букет из одной красной и двух розовых гвоздик можно составить
способами. По правилу произведения букет из одной красной и двух розовых гвоздик можно составить 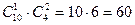 способами.
способами.
|
|
|


