 |
Простейший поток событий
|
|
|
|
Распределение Пуассона
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (p < 0, 1). В этих случаях (n велико, p мало) прибегают к асимптотической формуле Пуассона.
Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение np сохраняет постоянное значение, а именно, np =  . Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.
. Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.
Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:
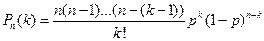
Так как np =  , то p =
, то p =  / n. Следовательно,
/ n. Следовательно,
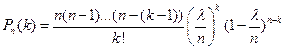
Приняв во внимание, что n имеет очень большое значение, вместо  найдем
найдем

 . При этом будет найдено лишь приближенное значение отыскиваемой вероятности поскольку n хотя и велико, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение np сохраняет постоянное значение, то при n
. При этом будет найдено лишь приближенное значение отыскиваемой вероятности поскольку n хотя и велико, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение np сохраняет постоянное значение, то при n  вероятность p
вероятность p  . Используя второй замечательный предел, имеем
. Используя второй замечательный предел, имеем
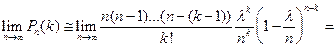
 =
=
 .
.
Таким образом,  =
=  .
.
Имеются специальные таблицы, пользуясь которыми можно найти  , зная k и
, зная k и  .
.
Примеры распределения Пуассона приведены на рис. 1
Математическое ожидание и дисперсия случайной величины X, подчиненной закону Пуассона, равны: M(X) =  , D(X) =
, D(X) =  .
.
Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 поврежденных изделия.
|
|
|
Решение. По условию, n = 5000, p = 0,0002, k = 3. Найдем  = np = 5000
= np = 5000  0,0002=1.
0,0002=1.
По формуле Пуассона искомая вероятность приближенно равна
 .
.
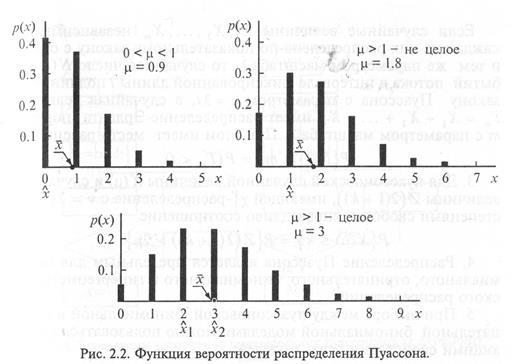
Примеры распределения Пуассона  приведены на рис. 1
приведены на рис. 1
Простейший поток событий
Рассмотрим события, которые наступают в случайные моменты времени.
Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и многие другие.
Среди свойств, которыми могут обладать потоки, выделим свойства стационарности, отсутствия последействия и ординарности.
Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k собы-тий на промежутках времени (1; 7), (10; 16), (Т; Т + 6) одинаковой длительности t = 6 ед. времени равны между собой.
Итак, если поток обладает свойством стационарности, то вероятность появления k событий за промежуток времени длительности t есть функция, зависящая только от k и t.
Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими слоя вами, условная вероятность появления k событий на любом промежутке времени, вычисленная при любых предположениях о том, что происходило до начала рассматриваемого промежутка (сколько событий появилось, в какой последовательности), равна безусловной вероятности. Таким образом, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.
|
|
|
Итак, если поток обладает свойством отсутствия последействия, то имеет место взаимная независимости появлений того или иного числа событий в непересекающиеся промежутки времени.
Свойство ординарности характеризуется тем, что no-s явление двух и более событий за малый промежуток времени практически невозможно. Другими словами вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью появления только одного события.
Итак, если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события.
Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности.
Замечание. Часто на практике трудно установить, обладает ли поток перечисленными выше свойствами. Поэтому были найдены и другие условия, при соблюдении которых поток можно считается простейшим или близким к простейшему. В частности, установлено, что если поток представляет собой сумму очень большого числа независимых стационарных потоков, влияние каждого из которых на всю сумму (суммарный поток) ничтожно мало, то суммарный поток (при условии его ординарности) близок к простейшему.
Интенсивностью потока  называют среднее число событий, которые появляются в единицу времени.
называют среднее число событий, которые появляются в единицу времени.
Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона
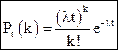
Эта формула отражает все свойства простейшего потока.
Действительно, из формулы видно, что вероятность появления k событий за время t, при заданной интенсивности является функцией k и t, что характеризует свойство стационарности.
Формула не использует информации о появлении событий до начала рассматриваемого промежутка, что характеризует свойство отсутствия последействия.
Убедимся, что формула отражает свойство ординарности. Положив k = 0 и k=1, найдем соответственно вероятности непоявления событий и появления одного события:
|
|
|
 ,
, 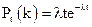
Следовательно, вероятность появления более одного события
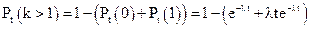
Пользуясь разложением
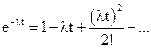
после элементарных преобразований получим
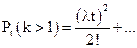
Сравнивая 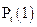 и
и  заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.
заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.
Итак, формулу Пуассона можно считать математической моделью простейшего потока событий.
Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятности того, что за 5 мин поступит: а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.
Решение. По условию,  = 2, t = 5, k = 2. Воспользуемся формулойПуассона
= 2, t = 5, k = 2. Воспользуемся формулойПуассона
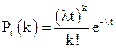
a) Искомая вероятность того, что за 5 мин поступит 2 вызова,
Р5 (2) = 102 • е - 10/2! = 100- 0,000045/2 = 0,00225.
Это событие практически невозможно.,
б) События «не поступило ни одного вызова» и «поступил один
вызов » несовместны, поэтому по теореме сложения искомая вероятность того, что за 5 мин поступит менее двух вызовов, равна
P5(k < 2) = P5(0) + P5(l) = e-10 + (10.e-10)/l!=0,000495.
Это событие практически невозможно.
в) События «поступило менее двух вызовов» и «поступило не менеедвух вызовов» противоположны, поэтому искомая вероятность того, что за 5 мин поступит не менее двух вызовов,
Р5 (k  2) = 1 — Р5 (k < 2) = 1 — 0,000495 = 0,999505. Это событие практически достоверно.
2) = 1 — Р5 (k < 2) = 1 — 0,000495 = 0,999505. Это событие практически достоверно.
Задача На АТС аварийной службы вызовы поступают в среднем 0,2 вызова в минуту. Для дискретной случайной величины – количество вызовов в течении 10 минут построить ряд распределения и график функции распределения, найти МО и D. Определить вероятность того, что количество вызовов будут не менее одного и не более чем три. Показать эту вероятность на графике функции распределения. Считать вызовы на АТС простейшим потоком Пуассона.
Решение
Пусть X - дискретной случайной величины – количество вызовов в течении 10 минут
 =0,2 вызова в минуту. t=10 минут
=0,2 вызова в минуту. t=10 минут
|
|
|
Вероятность для простейшего потока Пуассона определяется по формуле
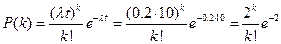
Составим закон распределения

| |||||||||||
| P | 0,135335 | 0,270671 | 0,270671 | 0,180447 | 0,090224 | 0,036089 | 0,01203 | 0,003437 | 0,000859 | 0,000191 | 3,82E-05 |
График функции вероятности

Найдем функцию распределения

График функции распределения
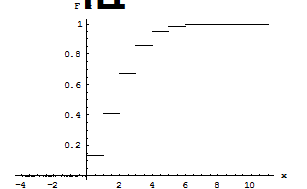
Математическое ожидание МО=  =2
=2
Дисперсия D=2
СКО= 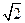
Вероятность того, что количество вызовов будут не более чем три.
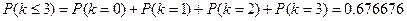
|
|
|


