Основные элементарные функции и их графики

Перечисленные ниже функции называют основными элементарными функциями; они наиболее употребительны в приложениях математики.

1°. y=C – const.для 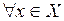, где Х – промежуток числовой прямой, её график при 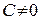– отрезок прямой, параллельной оси абсцисс.

2°. Показательная функция y =a^x, a ≠ 1, a > 0. Основные её свойства известны из курса элементарной математики: а) D (y)= R, E (y)= (0, + ∞);

б) при a> 1 показательная функция возрастает, при 0 < a < 1 она убывает. На рис. 8.1 изображены графики y =a^x при a > 1 и 0 < a <1.

3°. Логарифмическая функция y = log _a x, a ≠ 0, a > 0. Эта функция обратная по отношению к показательной функции y = a^x, в силу теоремы 7.1, её основные свойства следуют из свойств последней: а) D (y)=(0, + ∞), E (y) = R; б) при a > 1 функция y = log _a x возрастает, при 0 < a < 1 она убывает; в) график данной функции симметричен графику функции y = a^x относительно прямой y = x.

Графики y = log _a x при a > 1 и 0 < a <1 приведены на рис. 8.2.

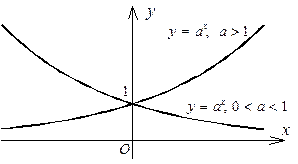
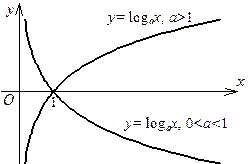
Рис. 8.1. Графики показательной Функции	Рис. 8.2. Графики логарифмической функции

 

4°. Степенная функция y = x^a, a 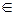R, a ≠ 0. При x >0 эту функцию рассмотрим как суперпозицию показательной и логарифмической функций: x^a =10 ^{a lg x} , lg x =log₁₀ x. Функции 10 ^x и lg x возрастают на (0, + ∞); тогда и y = x^a, a≠ 0, строго монотонна на (0, + ∞): возрастает при a >0 и убывает при a <0. При a >0 она определена в нуле: y (0) = 0. При некоторых значениях a (например, при a N) она определена на всей числовой оси. На

Рис. 8.3. Графики степенной функции при различных значениях a

5°. Тригонометрические функции y= sin x, y= cos x, y= tg x, y= ctg x.

Эти функции подробно рассмотрены в школьном курсе математики.

Их графики приведены на рис. 8.4 – 8.5.

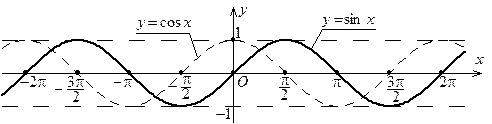
Рис. 8.4. Графики функций y = sin x и y = cos x

Рис. 8.5. Графики функций y = tg x и y = ctg x

6°. Обратные тригонометрические функции: y= arcsin x, y= arccos x, y= arctg x, y= arcctg x.

1. Функция y= arcsin x. По определению y= arcsin x – это угол (или

дуга) из промежутка [–π/2, π/2], синус которого равен х. Итак, y= arcsin x

– функция, обратная функции y= sin x, 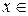[–π/2, π/2], основные её свойства следуют из свойств функции y= sin x, 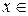[–π/2, π/2], и теоремы 7.1.

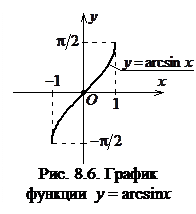а) D (y) = [−1, 1], E (y) = [–π/2, π/2];

б) y= arcsin x возрастает на D (y) от –π/2 до π/2;

в) y= arcsin x – нечётная функция:

arcsin(− x) = −arcsin x при ;

г) график функции y= arcsin x симметричен гра-фику функции y= sin x, x 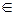[–π/2, π/2], относительно прямой у=х (рис. 8.6);

д) sin(arcsin x) = x при ,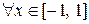

arcsin(sin x) = x при [–π/2, π/2].

2. Функция y= arccos x. По определению y= arccos x – это угол (или дуга) из промежутка [0, π], косинус которого равен х. Итак, y= arccos x – функция, обратная функции y= cos x, x 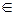[0, π], её основные свойства следуют из свойств функции y= cos x, x 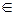[0, π] и теоремы 7.1.

а) D (y) = [−1, 1], E (y) = [0, π];

б) y= arccos x убывает на от π до 0;

в). y= arccos x не обладает свойствами чётности или нечётности:

arccos(− x)=π−arccos x; x 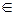[0, π];

г). график функции y= arccos x симметричен графику функции y= cos x, x 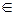[0, π]; относительно прямой у=х (рис. 8.7);

д). cos(arccos x) = x при 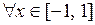, arccos(cоs x) = x при x 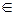(0, π).

3. Функция y= arctg x. По определению y= arctg x – это угол (или дуга) из промежутка (–π/2, π/2), тангенс которого равен х. Итак, y= arctg x – функция, обратная функции y= tg x, 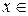(–π/2, π/2), поэтому её основные свойства можно вывести из свойств этой функции и теоремы 7.1:

а) D (y) = R, E (y) = (–π/2, π/2);

б) y= arctg x возрастает на D (y);

в) y= arctg x – нечётная функция: arctg(– x)= – arctg x при 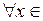R;

г) график функции y= arctg x симметричен графику функции y= tg x,

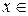(–π/2, π/2), относительно прямой у=х (рис. 8.8);

д) tg(arctg x) = x при 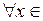R; arctg(tg x) = x при 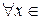.(– π / 2, π / 2)

4. Функция y= arcctg x. По определению y= arcctg x – это угол (или дуга) из промежутка (0, π), котангенс которого равен х. Таким образом, y= arctg x – функция, обратная функции y= ctg x, x 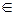(0, π), поэтому основные её свойства можно вывести из свойств этой функции и теоремы 7.1:

а). D (y) = R, E (y) = (0, π);

б). y= arcctg x убывает на D (y);

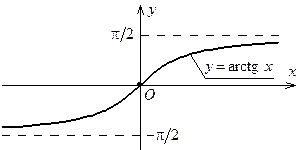
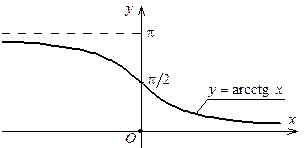
Рис. 8.8. График функции y= arctg x	Рис. 8.9. График функции y= arcсtg x

в). функция y= arcctg x не обладает свойствами чётности или нечётности, arcctg(− x)=π −arcctg x; x 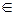R;

г). график функции y= arcctg x симметричен графику функции y= ctg x,

x 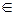(0, π), относительно прямой у=х (рис. 8.9);

д). ctg(arcctg x) = x при 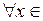R; arcctg(ctg x) = x при x 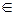(0, π).

Определение 8.1. Функция, которая может быть задана одним аналитическим выражением с помощью конечного числа суперпозиций и арифметических операций над основными элементарными функциями, называется элементарной функцией.

Элементарная функция называется алгебраической, если её можно задать конечным числом алгебраических действий (сложения, вычитания, умножения, деления и возведения в степень с рациональным показателем). Все другие элементарные функции называются трансцентдентными. Так, 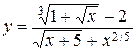= – алгебраическая функция, а

y = arctg 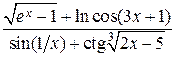– элементарная трансцентдентная функция.

Частным случаем алгебраической функции является так называемая рациональная функция R (x), представляемая в виде отношения двух многочленов: 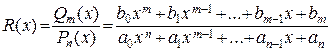. Если степень знаменателя 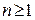, то рациональную функцию называют рациональной алгебраической дробью. В противном случае, т.е. при рациональная функция представляет собой многочлен (ибо , где R).

Поделиться:

Воспользуйтесь поиском по сайту: