Методика изучения неравенств в старших классах

Содержание

 

Введение. 3

1. Методика изучения темы "Неравенства" в начальной школе. 5

2. Методика изучения неравенств в старших классах. 11

2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики. 11

2.2 Классификация преобразований неравенств и их систем.. 13

2.3 Общая последовательность изучения материала линии неравенств. 15

3. Методика изучения основных классов неравенств и их систем.. 19

Заключение. 25

Список использованных источников. 27

 

Введение

 

Тема "Неравенства" занимает важное место в курсе алгебры. Она богата по содержанию, по способам и приемам решения неравенств, по возможностям ее применения при изучении ряда других тем школьного курса алгебры. Это объясняется тем, что уравнения и неравенства широко используются в различных разделах математики, в решении важных прикладных задач.

Анализ диссертационных работ, посвященных методике изучения темы "Неравенства" в основной школе, показал, что в настоящий момент имеется ряд исследований, раскрывающих ее различные аспекты. Одним из первых было диссертационное исследование К.И. Нешкова, в котором сформулированы принципы отбора содержания и выделен необходимый объем материала по теме. При этом большая роль отводилась упражнениям.

Исследования: М.В. Паюл, И.М. Степуро посвящены вопросам взаимосвязи понятий неравенства, уравнения и функции; М.П. Комова, Г.Н. Солтан - доказательствам и решению неравенств на геометрическом материале; Е.Ф. Недошивкина - внутрипредметным связям при изучении уравнений и неравенств в курсе математики 4-8-х классов; Н.Б. Мельниковой, Д.Д. Рыбдаловой - прикладным аспектам изучения неравенств в средней школе.

Итак, можно констатировать тот факт, что отдельные вопросы методики обучения понятию неравенства и решению конкретных неравенств в школьном курсе математики освещены достаточно полно.

Несмотря на значительный положительный опыт в методике преподавания темы "Неравенства", как показывает анализ результатов тестов, контрольных, выпускных, вступительных экзаменационных работ, учащиеся средней школы недостаточно полно владеют основными знаниями и умениями по решению неравенств. В качестве аргумента приведем анализ результатов участия России в международных исследованиях TIMSS (6-ое место из 36 стран участников), который показал, что наибольшую озабоченность по курсу алгебры вызывает качество знаний и умений учащихся по теме "Неравенства".

1. Методика изучения темы "Неравенства" в начальной школе.

 

Работа над неравенствами ведется с I класса, органически сочетаясь с изучением арифметического материала. Программа по математике для I-III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений "больше", "меньше", "равно"; научить записывать результаты сравнения с помощью знаков 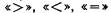и читать полученные неравенства.

Числовые неравенства учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками 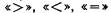 соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Если одно число больше (меньше) другого или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединенные соответствующим знаком, они образуют неравенство. Таким образом, первоначально у младших школьников формируются понятия только о верных неравенствах.

Однако в процессе работы над уравнениями, выражениями и неравенствами с переменной учащиеся, подставляя различные значения переменной, накапливают наблюдения и убеждаются в том, что равенства и неравенства бывают как верные, так и неверные. Такой подход к раскрытию понятий определяет соответствующую методику работы над равенствами, неравенствами, уравнениями.

Ознакомление с неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.

Сравнение осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствия. Этому способу сравнения множеств учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют перед числом 10; 5 больше, чем 4, потому что при счете число 5 называют после числа 4.

Установленные отношения записываются с помощью знаков 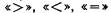, учащиеся упражняются в чтении и записи неравенств.

Впоследствии при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).

Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I-III классах предлагать разнообразные упражнения, например:

Подберите равную величину: 7 км 500 м = □ м, 3080 кг= □ т □ кг.

Подберите числовые значения величин так, чтобы запись верной: □ ч<□ мин, □ см =□ дм □ см, □ т □ ц =□ кг;

3) Вставьте наименование у величин так, чтобы запись была верной: 16 мин>16...

Подобные упражнения помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.

Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в сравнении выражения и числа (числа и выражения). Первые неравенства вида 3+1>3, 3-1<3 полезно получать из равенства (3=3), сопровождая преобразования соответствующими операциями над множествами. Например, на классном наборном полотне и на партах отложено 3 треугольника и 3 кружка и записано: 3=3. Учитель предлагает детям придвинуть к 3 треугольникам еще 1 треугольник и записать это (3+1 - запись под треугольниками). Число кружков не уменьшилось (3). Учащиеся сравнивают число треугольников и кружков и убеждаются, что треугольников больше, чем кружков (4>3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1<3 (три минус один меньше, чем три).

В дальнейшем выражение и число (число и выражение) учащиеся сравнивают, не прибегая к операциям над множествами; находят значение выражения и сравнивают его с заданным числом, что отражается в записях:

5+3>5 2<7-4 7=4+5

8>5 2<3 7=7

После знакомства с названиями выражений учащиеся читают равенства и неравенства так: сумма чисел 5 и 3 больше, чем число 5; число 2 меньше, чем разность чисел 7 и 4, и т.п.

Опираясь на операции над множествами и сравнение множеств, учащиеся практически усваивают важнейшие свойства равенств и неравенств (если а>b, то b<а).

Дети видят, что если кружков и треугольников поровну (рис.1), то можно сказать, что Кружков столько, сколько треугольников (3+2=5), а также треугольников столько, сколько кружков (5=3+2). Если же Предметов не поровну (рис.2), то одних - больше (3 + 1>3), а других меньше (3<3 + 1).

 

Рис.1 Рис.2

В дальнейшем при изучении действий в пределах 100, 1000 и 1000000, упражнения на сравнение выражения и числа даются на новом числовом материале и увеличивается количество чисел и знаков действий в выражениях.

Сравнивая неоднократно специально подобранные выражения и числа, например: 17+0 и 17, 19-0 и 19, 7-1 и 7, 0: 5 и 0, с+1 и с, с: 1 и с и т.п., учащиеся накапливают наблюдения об особых случаях действий, глубже осознают конкретный смысл действий. Упражнения на сравнение выражений и числа закрепляют умения читать выражения и способствуют выработке вычислительных навыков.

Сравнить два выражения, значит, сравнить их значения. Сравнение выражений впервые включается уже в конце изучения сложения и вычитания в пределах 10, а затем при изучении действий во всех концентрах эти упражнения систематически предлагаются учащимся. Например, надо сравнить Суммы: 6+4 и 6+3. Ученик рассуждает так: первая сумма равна 10, вторая-9, 10 больше, чем 9, значит, сумма чисел 6 и 4 больше, чем сумма чисел 6 и 3. Это рассуждение отражается в записях:

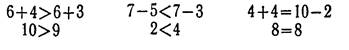
При изучении действий в других концентрах упражнения на сравнение выражений усложняются: более сложными становятся выражения, учащимся предлагаются задания вставить в одно из выражений подходящее число так, чтобы получить верные равенства или неравенства; проверить, верные ли равенства (неравенства) даны, неверные исправить, изменив знак отношения или число в одном из выражений; составить из данных выражений верные равенства или верные неравенства. Сами выражения подбираются таким образом, чтобы, сравнивая выражения, учащиеся наблюдали свойства и зависимости между компонентами и результатами действий. Например, после того как установили с помощью вычислений, что сумма 60+40 больше суммы 60+30, учитель предлагает сравнивать соответствующие слагаемые этих сумм, и дети отмечают, что первые слагаемые в этих суммах одинаковые, а второе слагаемое в первой сумме больше, чем во второй. Много раз, подмечая эту зависимость, учащиеся приходят к обобщению и затем свои знания используют при сравнении выражений.

Таким образом, при изучении всех концентров упражнения на сравнение чисел и выражений, с одной стороны, способствуют формированию понятий о равенствах я неравенствах, а с другой стороны, усвоению знаний о нумерация и арифметических действиях, а также выработке вычислительных навыков.

Неравенства с переменной вида: х+3<7, 10-х>5, х-4>12, 72: х<36 вводятся во II классе. Заранее ведется соответствующая подготовительная работа: включаются упражнения, в которых переменная обозначается не буквой, а "окошечком" (квадратом), например: □ >0, 6+4> □, 7+ □ <10 и т.д. Учащимся предлагается подобрать такое число, чтобы получить верную запись. При выполнении таких упражнений учитель должен побуждать детей к подстановке различных чисел; например, в неравенстве □ >0 можно подставить число 1 (1>□), можно 2 (2>□), можно З (3>□) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).

Рассматривая во II классе, например, неравенство х+3<10, учащиеся путем подбора находят, при каких значениях буквы х значение суммы х+3 меньше, чем 10. В каждом таком задании дается множество чисел - значений переменной. Ученики подставляют значения буквы в выражение, вычисляют значение выражения и сравнивают его с заданным числом. В результате такой работы выбирают значения переменной, при которых данное неравенство является верным.

Термины "решить неравенство", "решение неравенства" не вводятся в начальных классах, поскольку во многих случаях ограничиваются подбором только нескольких значений переменной, при которых получается верное неравенство.

Позднее в упражнениях с неравенствами значения переменной не даются, учащиеся сами подбирают их. Такие упражнения, как правило, выполняются под руководством учителя.

Можно ознакомить детей с таким приемом подбора значений переменной в неравенстве. Пусть дано неравенство 7×k<70. Сначала устанавливают, при каком значении k данное произведение равно 70 (при k=10). Чтобы произведение было меньше, чем 70, следует множитель брать меньше, чем 10. Учащиеся выполняют подстановку чисел 9, 8 и т.д. до нуля, вычисляют и сравнивают полученные значения выражения с заданным (70) и называют ответ.

Упражнения с неравенствами закрепляют вычислительные навыки, а также помогают усвоению арифметических знаний. Например, подставляя различные числовые значения компонентов, дети накапливают наблюдения об изменении результатов действий в зависимости от изменения одного из компонентов. Здесь уточняются знания детей о конкретном смысле каждого действия (так, подставляя значения вычитаемого, дети убеждаются в том, что вычитаемое не больше уменьшаемого и т.п.). Подбирая значения буквы в неравенствах и равенствах вида: 5+х=5, 5-х=5; 10×х=10, 10×х<10, учащиеся закрепляют знания особых случаев вычислений. Работая с неравенствами, учащиеся закрепляют представление о переменной и подготавливаются к решению неравенства в IV классе.

В соответствии с программой в I-III классах рассматриваются уравнения первой степени с одним неизвестным вида:

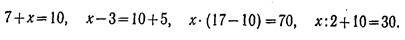
Неизвестное число сначала находят подбором, а позднее на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями.

Методика изучения неравенств в старших классах

 

Содержание и роль линии уравнений и неравенств в современном школьном курсе математики

 

Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно-методическую линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой, функциональной и другими линиями школьного курса математики.

Выделенным областям возникновения и функционирования понятия уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.

а) Прикладная направленность линии уравнений и неравенств раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.

б) Теоретико-математическая направленность линии уравнений и неравенств раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, неравенств и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений и неравенств связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений и неравенств.

в) Для линии уравнений и неравенств характерна направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией. Основная идея, реализуемая в процессе установления взаимосвязи этих линий, - это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений, неравенств, систем. Например, числовые промежутки выделяются неравенствами или системами неравенств. Области иррациональных и логарифмических выражений связаны соответственно с уравнениями 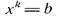 (k-натуральное число, большее 1) и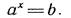

Связь линии уравнений и неравенств с числовой линией двусторонняя. Приведенные примеры показывают влияние уравнений и неравенств на развертывание числовой системы. Обратное влияние проявляется в том, что каждая вновь введенная числовая область расширяет возможности составления и решения различных уравнений и неравенств.

Линия уравнений и неравенств тесно связана также и с функциональной линией. Одна из важнейших таких связей приложения методов, разрабатываемых в линии уравнений и неравенств, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т.д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: