 |
Эвристический алгоритм состоит из следующих шагов
|
|
|
|
УЛМ
| x2 | x1 | x0 | y |
Составить таблицу истинности (начальное значение выходов тригерров равно 0)
| x3 | x2 | x1 | x0 | Q0JK | Q0T | y0 | y1 |
Гонки комбинационных схемах.
Инерционность элементов и наличие различных факторов, приводящих к задержке распространения сигнала, приводят к задержке появления выходных сигналов КУ, т.е. сигналы на выходе КУ, соответствующие новому состоянию входных сигналов, появляются не сразу, а с некоторой задержкой.
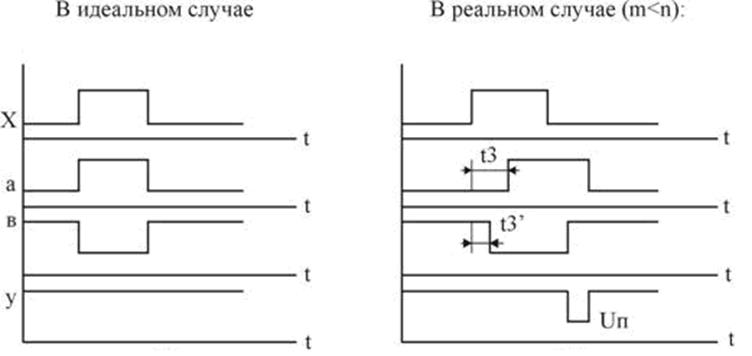
Борьба с гонками.
Существует три наиболее часто встречающихся способа борьбы с гонками:
- Синхронизация структурного автомата
- Учет минимального времени задержки распространения сигнала
- Построение противогоночных схем
- Направленное кодирование состояний абстрактного автомата
|
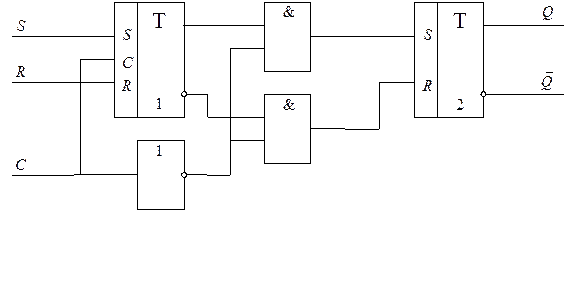
Кодирование внутренних состояний ЦА
Кодирование заключается в сопоставлении каждому состоянию автомата набора (кода) состояний элементов памяти.
010 -> 100
T1: 0 -> 1
T2: 1 -> 0
T3: 3 -> 0
Гонки в автомате
|
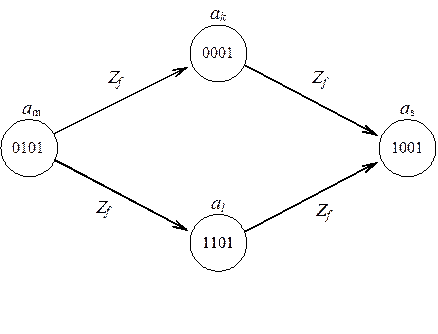
- некритическими
- критическими состязаниями
|
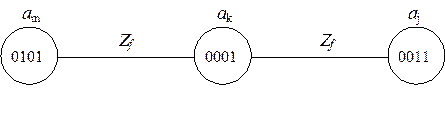
Соседнее кодирование
- в графе автомата не должно быть циклов с нечетным числом вершин;
- два соседних состояния второго порядка не должны иметь более двух состояний, лежащих между ними.
|
| a 1 | a 2 | a 3 | a 7 | |
| a 6 | a 4 | a 5 |
|
|
|
a 1 ~ 000
a 2 ~ 010
a 3 ~ 110
a 4 ~ 111
a 5 ~ 101
a 6 ~ 001
a 7 ~ 100 
Кодирование состояний
- алгоритм кодирования для D -триггеров;
- эвристический алгоритм кодирования.
Алгоритм кодирования для D -триггеров
- Каждому состоянию автомата а m (m = 1,2,..., M) ставится в соответствие целое число N m, равное числу переходов в состояние а m (N m равно числу появлений а m в поле таблицы переходов или числу дуг, входящих в а m при графическом способе задания автомата).
- Числа N 1, N 2,..., N m упорядочиваются по убыванию.
- Состояние а s с наибольшим N s кодируется кодом: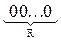 
, где R -количество элементов памяти.
- Следующие R состояний согласно списка пункта 2 кодируются кодами, содержащими только одну 1: 00... 01, 00... 10,..., 01... 00, 10... 00.
- Для оставшихся состояний опять в порядке списка п.2. используют коды с двумя единицами, затем с тремя и так далее пока не будут закодированы все состояния.
| a 1 | a 2 | a 3 | a 4 | a 5 | a 1 | a 2 | a 3 | a 4 | a 5 | |||
| Z 1 | a 1 | a 1 | a 5 | a 3 | a 1 | Z 1 | w 1 | w 2 | w 1 | w 1 | w 1 | |
| Z 2 | a 2 | a 3 | a 2 | a 3 | a 3 | Z 2 | w 1 | w 3 | w 4 | w 2 | w 2 | |
| Z 3 | a 3 | a 4 | a 2 | a 4 | a 2 | Z 3 | w 2 | w 2 | w 2 | w 1 | w 3 |
a 1 ~ N 1 = 3 N 3 a 3 = 000
a 2 ~ N 2 = 4 N 2 a 2 = 001
a 3 ~ N 3 = 5 N 1 a 1 = 010
a 4 ~ N 4 = 5 N 4 a 4 = 100
a 5 ~ N 5 = 1 N 5 a 5 = 011
w 1 ~ N 1 = 6 N 1 w 1 = 00
w 2 ~ N 2 = 5 N 2 w 2 = 01
w 3 ~ N 3 = 2 N 3 w 3 = 10
w 4 ~ N 4 = 2 N 4 w 4 = 11
Эвристический алгоритм кодирования
определения
- Вершины графа отождествляются с состояниями автомата
- Вершины i и j соединены ребром, если есть переход из аi и аj или наоборот
- q (i, j) - число всевозможных переходов автомата из аi в аj
- вес ребра р (i, j) = q (i, j) + q (j, i)
- w (i, j) = р (i, j)× d (i, j), где d (i, j) – число компонентов, которыми коды состояний аi в аj отличаются друг от друга
| a 1 | a 2 | a 3 | a 4 | a 5 | ||
| Z 1 | a 1 | a 1 | a 5 | a 3 | a 1 | |
| Z 2 | a 2 | a 3 | a 2 | a 3 | a 3 | |
| Z 3 | a 3 | a 4 | a 2 | a 4 | a 2 |
|
Эвристический алгоритм состоит из следующих шагов
1. Строим матрицу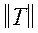 
, состоящую из всех пар номеров (i, j), для которых р (i, j) ¹ 0 и i < j. Для каждой пары в матрице 
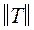указываем ее вес р (i, j), совпадающий с весом ребра соединяющего а i и а j.
|
|
|
| i | j | p(i,j) | ||
| T | = | |||
2. Упорядочим строки матрицы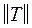 
, для чего построим матрицу 
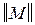следующим образом. В первую строку матрицы 
поместим пару (a,b) с наибольшим весом р (a,b). В нашем случае (a,b) = (2,3), р (2,3) = 3. Из всех пар, имеющих общий компонент с парой (a,b) выбирается пара (g,d) с наибольшим весом и заносится во вторую строку матрицы 
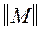. Ясно, что { a,b }×{ g,d }¹0. Затем из всех пар, имеющих общий компонент хотя бы с одной из внесенных уже в матрицу 
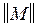пар выбирается пара с наибольшим весом и заносится в матрицу 
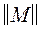и т.д..
В случае равенства весов пар вычисляются суммы весов компонентов пар (весом р (a) компонента a называется число появлений a в матрице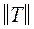 
) и в матрицу 
заносится пара с наибольшей суммой весов.
(2,3) с p (2,3)=3;
(1,2) с р (1,2) = 2; (3,4) с р (3,4) = 2, (3,5) с р (3,5) = 2;
р (1) = 3 р (2) = 3 р (1) + р (2) = 6
р (3) = 4 р (4) = 2 р (3) + р (4) = 6
р (3) = 4 р (5) = 2 р (3) + р (5) = 6
| i | j | p(i,j) | ||
| M | = | |||
3. Определяем разрядность кода для кодирования состояний автомата (количество элементов памяти – триггеров). Всего состояний M=5. Тогда
R = log2M = log25 =3
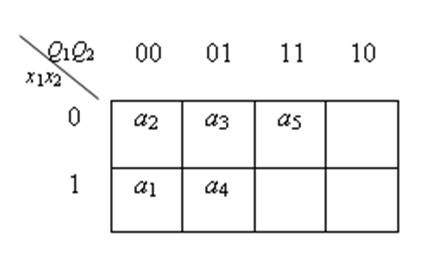
Закодируем состояния из первой строки матрицы следующим образом: K 2 = K (а 2) = 000; K 3 = K (а 3) = 001.
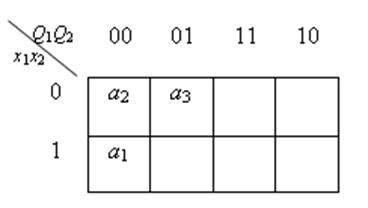
Для удобства кодирования будем иллюстрировать этот процесс картой Карно:
|
4. Вычеркнем из матрицы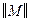 
первую строку, соответствующую закодированным состояниям а 2 и а 3. Получим матрицу .
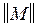| i | j | p(i,j) | ||
| M’ | = | |||
5. В силу упорядочивания п.2 в первой строке закодирован ровно один элемент. Выберем из первой строки незакодированный элемент и обозначим его g. (В нашем случае g = 1).
6. Строим матрицу 
, выбрав из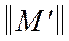 
строчки, содержащие g.
|
|
|
| i | j | p(i,j) | ||||
| M g | = | M’ | = | |||
Пусть Bg = { g 1,..., gF } – множество элементов из матрицы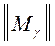 
, которые уже закодированы. Их коды Кg 1,..., KgF соответственно. В нашем случае:
Bg = B 3 = {2,3} K 2 = 000 K 3 = 001.
7. Для каждого Kg f (f =1,..., F) найдем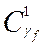 
– множество кодов, соседних с 
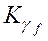и еще не занятых для кодирования состояний автомата. (Для соседних кодов кодовое расстояние d=1).
K 2 = 000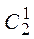 
= {100, 010}
K 3 = 001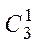 
= {011, 101}.
Построим множество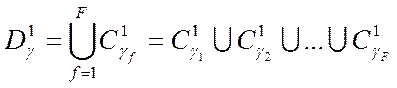 
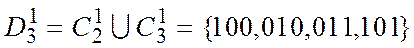
Если оказывается, что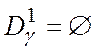 
, то строим новое множество 
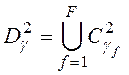, где 
– множество кодов, у которых кодовое расстояние до кода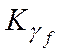 
равно 2 и т.д..
8. Для каждого кода из множества Dg находим кодовое расстояние до кода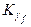 
.
K 2 = 000 K 3 = 001
d (100, 000) = 1 d (100, 001) = 2
d (010, 000) = 1 d (010, 001) = 2
d (011, 000) = 2 d (011, 001) = 1
d (101, 000) = 2 d (100, 001) = 1
9. Находим значение функции w для каждого кода из множества Dg.
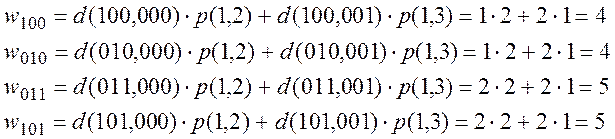
10. Из множества Dg выбираем код Kg, у которого получилось минимальное значение w в п.9. Выбираем код для состояния a 1 К 1 =100.
11. Из матрицы 
вычеркиваем строки, в которых оба элемента уже закодированы, в результате чего получим новую матрицу 
. Если в новой матрице 
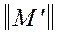не осталось ни одной строки, то кодирование закончено. В противном случае возвращаемся к п.5. В нашем случае имеем:
| i | j | p(i,j) | ||
| M’ | = | |||
К 2 = 000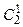 
= {010}
K 3 = 001 
= {011, 101}
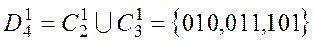
K 2 = 000 K 3 = 001
d (010, 000) = 1 d (010, 001) = 2
d (011, 000) = 2 d (011, 001) = 1
d (101, 000) = 2 d (101, 001) = 1
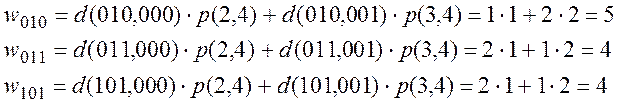
Выбираем К 4 = 101.
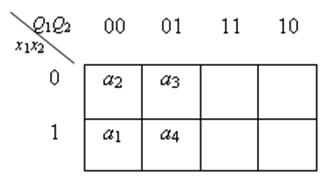
К 1 = 100 
= {110}
K 2 = 000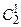 
= {010}
К 3 = 001 = {011}
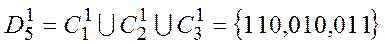
К 1 = 100 K 2 = 000 K 3 = 001
d (110, 100) = 1 d (110, 000) = 2 d (110, 001) = 3
d (010, 100) = 2 d (010, 000) = 1 d (010, 001) = 2
d (011, 100) = 3 d (011, 000) = 2 d (011, 001) = 1
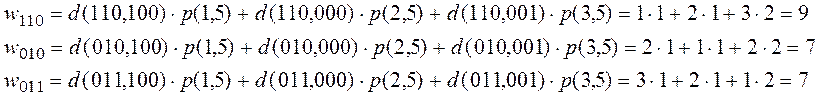
Выбираем К 5 = 011.
|
|
|
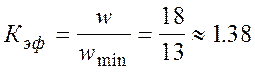
