 |
Раздел «Теоретическая механика»
|
|
|
|
В задачах статики приходится рассматривать равновесие несвободных тел, лишенных возможности перемещаться в направлении действия приложенных к ним так называемых активных сил. Тела, ограничивающие движение рассматриваемого тела, называются связями. Между телом и связью на основании закона равенства действия и противодействия возникают равные и противоположно направленные силы взаимодействия.
Сила, с которой связь действует на рассматриваемое тело, называется реакцией связи или просто реакцией.
Сила, с которой тело действует на связь, называется силой давления на связь. Таким образом, сила реакции и сила давления на связь – две равные по модулю силы, имеющие противоположное направление.
Задачи на равновесие несвободных тел решаются втакой последовательности:
1. Выяснить, какое тело (точка) в данной задаче находится всостоянии равновесия, и приложить к нему заданные силы.
2. Выделенное тело освободить от связей и их действие заменить силами реакций.
3. Выбрать направление координатных осей.
4. Составить уравнения равновесия в одном из двух видов: Σ xi = 0; ΣМA=0; ΣМВ= 0; либо ΣХi= 0; ΣYi=0; ΣМВ = 0.
5. Решить уравнения равновесия.
6. Проверить правильность решения задачи.
Методику решения задач с помощью уравнений равновесия рассмотрим на примерах.
Для решения первой задачи (№ 1-20), которая относится к теме 1.2 «Плоская система произвольно расположенных сил», требуется составить уравнения проекций на координатные оси и уравнения моментов.
Проекция вектора – скалярная величина, которая определяется отрезками, отсекаемыми перпендикулярами, опущенными из начала и конца вектора на ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси (рис. 1, а), и отрицательной (—) если проекция направлена в противоположную сторону (рис. 1,б).
|
|
|
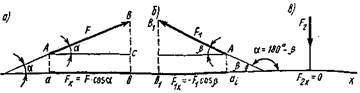
Рис. 1
Моментом силы относительно точки называется произведение модуля силы на плечо, т. е. на длину перпендикуляра, восставленного из точки, относительно которой берется момент, к линии действия силы. Момент принято считать положительным, если он стремится повернуть тело по часовой стрелке (рис. 2, а), и отрицательным (рис. 2, б), если вращение направлено в противоположную сторону.
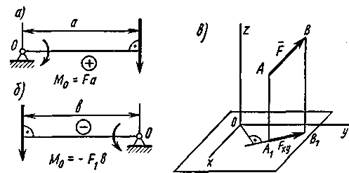
Рис. 2
Между моментом пары и моментами сил пары относительно любой точки существует такая важная зависимость: алгебраическая сумма моментов сил пары относительно любой точки — величина постоянная для данной пары и равна ее моменту. Так как пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой.
Момент пары сил в СИ выражается в ньютонометрах (Н·м) или в единицах, кратных ньютонометру: кН·м, МН·м и т. д.
Пример 1. Однородная балка закреплена в точке А с помощью шарнирно-неподвижной опоры и поддерживается в точке В стержнем (рис. 3, а). Найти реакции шарнирно-неподвижной опоры и стержня ВС. Силой тяжести балки и стержня пренебречь.
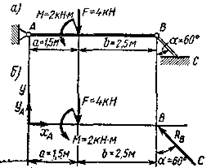
Рис. 3
При рассмотрении пространственной системы сил необходимо ввести понятие о моменте силы относительно оси.
Моментом силы относительно оси называется алгебраическая (скалярная) величина, равная моменту проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с плоскостью.
Последовательность определения момента силы F относительно оси z (рис. 2, в): а) задают модуль и направление силы F; б) указывают координатные оси; в) перпендикулярно оси выбирают плоскость XOY; г) силу F проецируют на эту плоскость и определяют модуль Fxy этой проекции; д) опустив перпендикуляр из начала координат на проекцию Fxy, определяют плечо а = О К; е) определяют момент M2(F) = Fxya.
|
|
|
Момент силы относительно оси равен нулю, если сила и ось лежат в
одной плоскости: а) сила действует вдоль оси; б) сила F пересекает
ось z; в) сила F параллельна оси z.
Решение. Изобразим балку вместе с нагрузками, соблюдая заданные размеры ее участков и угла а (рис. 3, б).
Освободим балку от связей в точках А и В, заменив эти связи их реакциями. Начало координат поместим в точке А, ось х совместим с осью балки, а ось у направим перпендикулярно балке. Если стержень растягивается, то его реакция направлена в сторону от рассматриваемого тела, а при сжатии – от стержня к телу.
Составим три уравнения равновесия:
Σ Xi = 0 – алгебраическая сумма проекций сил на ось х;
Σ Yi = 0 – алгебраическая сумма проекций сил на ось у;
Σ МА = 0 – алгебраическая сумма моментов относительно точки А.
Уравнение проекций сил на ось х имеет вид
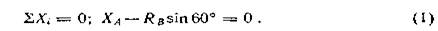
Силы F и YA не вошли в уравнение, так как они перпендикулярны оси х и их проекции на эту ось равны нулю. Проекции силы на ось у

реакция ХА перпендикулярна оси у и ее проекция на эту ось равна нулю. Для составления уравнения моментов за центр моментов принимаем точку А. Плечо силы RB равно длине перпендикуляра, восставленного из точки А (центра моментов) к линии действия силы RB. Из рис. 3, б видно, что AD = (а + b)cos60°.

Подставив числовые значения, получим
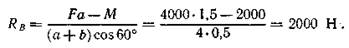
Выразим из (2)
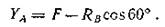
Подставив значения сил, получим
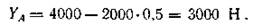
Из (1)
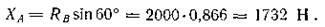
Проверим правильность решения задачи, составив уравнения моментов относительно точки В:
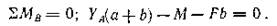
Подставим числовые значения 3000 • 4 – 2000 – 4000 • 2,5 = 0; 12000 – 12000 = 0.
Задача решена верно, так как при подстановке получили тождество 0 = 0.
Вторую задачу контрольной работы (№ 21-30) можно решать после изучения тем 1.3 «Пара сил» и 1.4 «Плоская система произвольно расположенных сил».
Напомним, что в шарнирно-подвижной опоре А реакция направлена по нормали к опорной поверхности (рис. 4, б). Модуль и направление реакции шарнирно-неподвижной опоры В неизвестны. В этом случае реакцию RB заменяют двумя составляющими: вертикальной YB и горизонтальной Хв. Освобожденная от связей балка изображена на рис. 4, б. Порядок решения подобных задач такой же, как в примере 1.
|
|
|
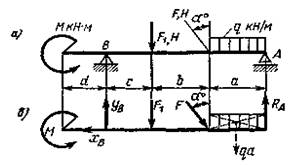
Рис. 4
Пример 2. Для балки (рис. 5, а)определить опорные реакции по следующим данным: а =1,5 м, b = 1 м, с = 2 м, F1 = 8 кН, F2 = 10 кН, q = 0,4 кН/м, М = 5 кН·м.
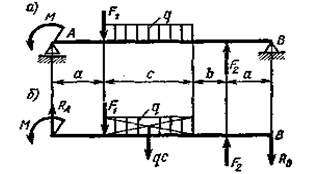
Рис. 5
Решение. Освободим балку от связей, отбросив опоры и приложив вместо них неизвестные реакции (рис. 5, б). Напомним, что для плоской системы параллельных сил достаточно двух уравнений равновесия:
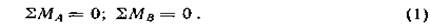
Уравнения моментов относительно точки А:
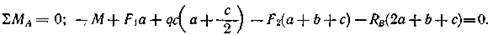
Уравнение моментов относительно точки В:
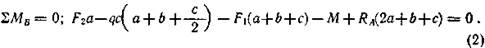
Из первого уравнения
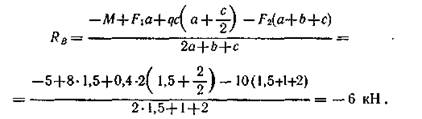
Из второго уравнения

Значение реакции RB получено со знаком минус. Это означает, что она направлена вертикально вниз.
Для проверки правильности найденных реакций опор балки составляем уравнение ΣY=0; RA – F 1 – qc+F2+RB = 0, или 4,8 – 8 – 2·0,4+10 – 6 = 14,8 – 14,8 = 0.
Следовательно, RA и RB определены верно.
Третью задачу контрольной работы (31-40) решать после изучения темы 1.6 «Центр тяжести». В этих задачах требуется находить центр тяжести плоских фигур, составленных из простых геометрических фигур. Положение центра тяжести плоской фигуры определяется по формулам:

где хс и yс – искомые координаты центра тяжести фигуры; xi и yi – координаты центров тяжести составных частей фигуры, которые определяются из заданных размеров; Аi – площади составных частей.
Последовательность решения таких задач рассмотрена в примере.
Пример 3. Вычислить координаты центра тяжести сечения плоской фигуры (рис. 6, а).
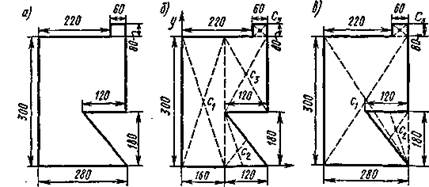
Рис. 6
Решение. Заданную плоскую фигуру разбиваем на составные части, центры тяжести которых легко определяются (рис. 6, б)– прямоугольник I, треугольник II и прямоугольники III и IV.
Располагаем координатные оси, как показано на рис. 6, а.
Находим площади каждой части и координаты хс и ус их центров тяжести Сi. Все эти данные заносим в табл. 2.
Вычисляем координаты хс и ус центра тяжести плоской фигуры:

Таблица 2
| Составная часть | Площадь составной части Ai, мм2 | Координаты центров тяжести каждой части | |
| xi, мм | yi, мм | ||
| I | 300·160 = 48000 = 48·103 | ||
| II | 1/2·120·180=10800= = 10,8·103 | 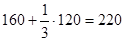
| 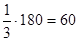
|
| III | 120·120=14400=14,4·103 | 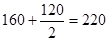
|  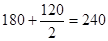
|
| IV | 80·60= 4800= 4,8·103 | 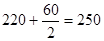
| 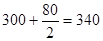
|
|
|
|
При решении задач можно использовать метод отрицательных площадей, как это показано на рис. 6, в. Здесь данная фигура разделена на три части: прямоугольники I и III и треугольник II, причем площадь треугольника II, вырезанная из плоской фигуры, берется со знаком минус, т. е. считается отрицательной. Легко проверить, что если при таком разделении фигуры все исходные данные свести в табл. 3 и выполнить вычисления, то получится тот же результат.
Таблица 3
| Составная часть | Площадь составной части Ai, мм2 | Координаты центра тяжести каждой части | |
| xi, мм | yi, мм | ||
| I | 300·280=84000=84·103 | 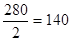
| 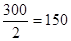
|
| II | 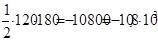 =10,8·103 =10,8·103
| 
| 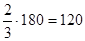
|
| III | 60·80=4800=4,8·103 | 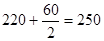
| 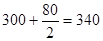
|
Определяем
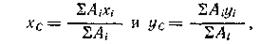

Центр тяжести тела в обоих случаях совпадает, что указывает на правильность решения задачи.
Четвертую задачу контрольной работы (№ 31-40) следует решать после изучения тем 1.7 «Основные понятия кинематики» и 1.8 «Кинематика точки». В задачах рассматривается равнопеременное движение точки. Следует учесть, что при использовании уравнения равнопеременного движения точки s = v0t + (a,t2/2)по криволинейной траектории кроме касательного ускорения у точки возникает нормальное ускорение ап = v2/p, направленное по радиусу кривизны траектории к ее центру.
Для решения задач используются соответствующие готовые уравнения и формулы, выведенные в учебниках (см. приложение, табл. П. 1).
Решение задач целесообразно иллюстрировать рисунками.
Пример 4. По дуге радиусом r = 1200 м (рис. 7) движется поезд, его скорость в. начале движения по дуге составляет vo = 60 км/ч.
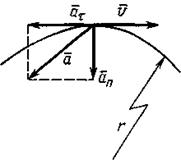
Рис. 7
После того как поезд прошел расстояние 800 м, его скорость уменьшилась до 36 км/ч. Определить полное ускорение в начале и конце движения.
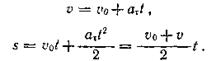
Из первого уравнения
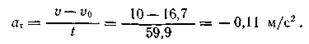
Решение. Определим касательное ускорение из уравнений:
Из второго уравнения
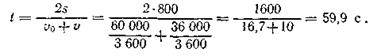
Так как движение равномерно замедленное, то касательное ускорение в течение всего времени движется постоянно.
Найдем нормальное ускорение:
в начале движения аn = 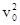 / r = 16,72/1200= 0,23 м/с2;
/ r = 16,72/1200= 0,23 м/с2;
в конце движения аn = v2/r = 102/ 1200 = 0,08 м/с2;
полное ускорение:
в начале движения 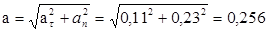 м/с2;
м/с2;
в конце движения  м/с2.
м/с2.
Пример 5. Точка движется прямолинейно по закону s=t4+2t (s – в метрах, t – в секундах). Найти ее среднее ускорение в промежутке между моментами ti = 2 с и t2 = 4 с, а также истинное ускорение в момент t3 = 3 с.
Решение. Сначала определим скорость точки
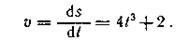
Подставив вместо t его значения t1 = 2 с и t2 = 4 с, находим
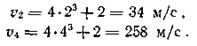
Следовательно, приращение скорости за данный промежуток времени
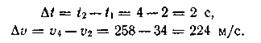
Среднее ускорение точки
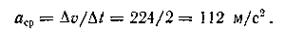
Для определения ускорения точки в любой момент времени возьмем производную от скорости по времени
|
|
|
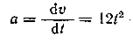
и подставим в это уравнение вместо t его значение t3 = 3 с:
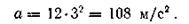
Пятую задачу контрольной работы (№ 41-50) следует решать после изучения тем 1.9 «Простейшие движения твердого тела», 1.12 «Основные понятия и аксиомы динамики», 1.13 «Метод кинетостатики для материальной точки». Шестую задачу контрольной работы (№ 51-60) следует решать после изучения тем 1.14 «Работа и мощность», 1.15 «Теоремы динамики». Рассматривая вращательное движение твердого тела, необходимо отчетливо уяснить, что вращение тела характеризуется угловыми величинами (угол поворота φ, угловая скорость ώ и угловое ускорение ε), а отдельные точки вращающегося тела совершают криволинейное движение (по окружностям) и их движение характеризуется линейными величинами (путь s, скорость v и ускорение aτ, an).
При решении задач динамики необходимо пользоваться принципом Даламбера, с помощью которого задачи динамики решаются с использованием уравнения равновесия статики. Согласно принципу Даламбера, в каждый данный момент действующие на материальную точку силы уравновешиваются силами инерции.
При решении задач рекомендуется такая последовательность: 1) выделить точку, движение которой рассматривается в данной задаче; 2) выяснить, какие активные силы действуют на точку и изобразить их на рисунке; 3) освободить точку от связей, заменив их реакциями; 4) к образовавшейся системе сил добавить силу инерции, помня, что направлена она по линии вектора ускорения точки, но в противоположную сторону; 5) выбрать расположение осей координат и составить два уравнения проекций всех сил на эти оси (ΣXi = 0; ΣYi = 0); 6) решив уравнения, определить искомые значения величин.
Пример 6. Маховик диаметром 0,8 м начинает вращаться из состояния покоя. Через 10 с после начала движения скорость точек обода маховика достигает 8 м/с. Определить ускорение этих точек. Чему равно число оборотов маховика за первые 10 с равнопеременного вращения?
Решение. По значению скорости точки находим угловую скорость вращения маховика через 10 с после начала вращения:
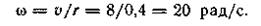
Угол поворота маховика за 10 с
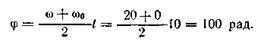
Число оборотов маховика за 10 с
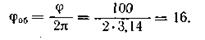
Угловое ускорение маховика
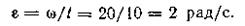
Нормальное ускорение точек обода маховика в момент t = 10
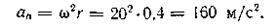
Касательное ускорение точек обода маховика
аτ = εr = 2·0,4 = 0,8 м/с2.
Пример 7. Груз массой 200 кг (рис. 8) опускается равноускоренно с помощью невесомого троса, перекинутого через блок, и в первые 5 с проходит 10 м. Определить силу натяжения троса.
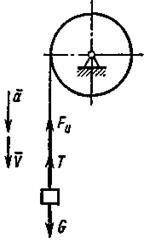
Рис. 8
Решение. Обозначив груз точкой А, приложим к нему силу тяжести G, реакцию троса Т и добавим к ним силу инерции Fи направив ее в сторону, противоположную ускорению.
Ускорение а определяем из уравнения равнопеременного движения s = at2/2, так как начальная скорость v0 = 0:
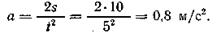
Согласно принципу Даламбера, силы G, Т и Fи находятся в равновесии, т.е. Т +Fи – G = 0, откуда Т= G – Fи. Выражая силу инерции и силу тяжести через массу груза (Fи = ma, G = mg), получаем T = mg – ma = m(g – a) = 200(9,81 – 0,8) = 1802 H.
Пример 8. Для остановки поезда, движущегося по прямолинейному участку пути со скоростью v = 10 м/с, производится торможение. Через сколько секунд остановится поезд, если при торможении развивается постоянная сила сопротивления, равная 0,02 силы тяжести поезда? Какой путь пройдет поезд до остановки?
Решение. Поезд совершает поступательное движение. Рассматривая его как материальную точку М (рис. 9), движущуюся в направлении оси Ох, укажем действующие силы: G – сила тяжести поезда, R – нормальная реакция рельсов, F – сила сопротивления, направленная противоположно вектору скорости. Силы G и R уравновешиваются согласно аксиоме действия и противодействия.
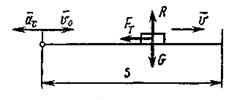
Рис. 9
По теореме об изменении количества движения материальной точки в проекции на ось Ох
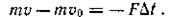
Так как F = 0,02G = 0,02mg, to = 0, vo = 10 м/с, v = 0, получим – mvo = – 0,02mg Δ t.
Откуда
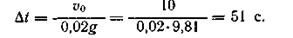
Для определения пройденного пути поездом до его остановки воспользуемся теоремой об изменении кинетической энергии:
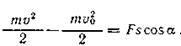
Работа силы торможения отрицательна (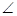 а =
а = 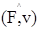 = 180° и cosa = – 1), поэтому
= 180° и cosa = – 1), поэтому
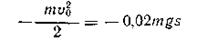
и путь, пройденный поездом:
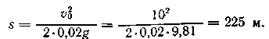
|
|
|


