 |
Решение типового примера.
|
|
|
|
Пусть имеются данные:
| t | |||||||||
| Y(t) | |||||||||
| X(t) |
Решение:
1. Для зависимой переменной Y(t) построим линейную однопараметрическую модель регрессии 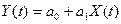 .
.
Итак, мы имеем данные о динамике изменения двух показателей за девять периодов, числовые значения которых приведены в первых трех графах таблице 9.
Таблица 9. Оценка параметров уравнения регрессии.

| 
| 
| 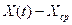
| 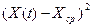
| 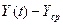
| 
| 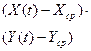
| 
| 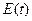
|
| -22,9 | 524,41 | -7,7 | 59,29 | 176,33 | 12,8 | -0,8 | |||
| -15,9 | 252,81 | -4,7 | 22,09 | 74,73 | 14,9 | 0,1 | |||
| -12,9 | 166,41 | -3,7 | 13,69 | 47,73 | 15,8 | 0,2 | |||
| -1,9 | 3,61 | -0,7 | 0,49 | 1,33 | 19,1 | -0,1 | |||
| 2,1 | 4,41 | -1,7 | 2,89 | -3,57 | 20,3 | -2,3 | |||
| 8,1 | 65,61 | 0,3 | 0,09 | 2,43 | 22,1 | -2,1 | |||
| 10,1 | 102,01 | 4,3 | 18,49 | 43,43 | 22,7 | 1,3 | |||
| 12,1 | 146,41 | 5,3 | 28,09 | 64,13 | 23,3 | 1,7 | |||
| 21,1 | 445,21 | 8,3 | 68,89 | 175,13 | |||||
| 1710,89 | 214,01 | 581,67 |
Оценка параметров модели регрессииосуществляется МНК на основе следующих формул:
 (15)
(15)
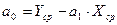 (16)
(16)
Воспользуемся этими формулами, а необходимые промежуточные результаты вычислений приведем в таблице 9.

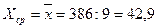
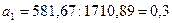
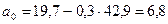
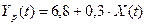 ,
,  (17)
(17)
Расчетные значения определяются путем последовательной подстановки в эту модель значения фактора:

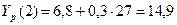 и т.д.
и т.д.
2. Оценим качество построенной модели, исследовав ее адекватность и точность.
а) Модель является адекватной, если ряд остатков обладает свойствами случайности, независимости последовательных уровней и нормальности распределения. Результаты исследования адекватности отражены в таблице 10.
Таблица 10. Оценка адекватности модели.
| t | Отклонение 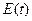
| Точки поворота | 
| 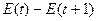
| 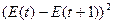
| 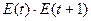
| 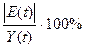
|
| -0,8 | 0,64 | -0,9 | 0,81 | -0,08 | 6,7 | ||
| 0,1 | 0,01 | -0,1 | 0,01 | 0,02 | 0,7 | ||
| 0,2 | 0,04 | 0,3 | 0,09 | -0,02 | 1,3 | ||
| -0,1 | 0,01 | 2,2 | 4,84 | 0,23 | 0,5 | ||
| -2,3 | 5,29 | -0,2 | 0,04 | 4,83 | 12,8 | ||
| -2,1 | 4,41 | -3,4 | 11,56 | -2,73 | 10,5 | ||
| 1,3 | 1,69 | -0,4 | 0,16 | 2,21 | 5,4 | ||
| 1,7 | 2,89 | -0,3 | 0,09 | 3,4 | 6,8 | ||
| 7,1 | |||||||
| 18,98 | -2,8 | 17,6 | 7,86 | 51,7 |
1). Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек. В соответствии с ним каждый уровень ряда сравнивается с двумя рядом стоящими. Если он больше или меньше их, то эта точка считается поворотной. Далее подсчитывается сумма поворотных точек "р". В случайном ряду чисел должно выполняться строгое неравенство (4):
|
|
|
При n = 9 в правой части неравенства имеем:
 .
.
В таблице 7 в третьей графе для первого и последнего наблюдения проставим прочерк, ноль — если точка неповоротная, и единицу, если она поворотная. В нашем примере количество поворотных точек равно четырем (р =2), неравенство (4) не выполняется, следовательно, свойство случайности не выполняется.
2). При проверке независимости (отсутствия автокорреляции) определяется отсутствие в ряду остатков систематической составляющей. Это проверяется с помощью  -критерия Дарбина - Уотсона, в соответствии с которым вычисляется коэффициент d формула (5).
-критерия Дарбина - Уотсона, в соответствии с которым вычисляется коэффициент d формула (5).
Вычисленная величина этого критерия сравнивается с двумя табличными уровнями (нижним 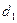 и верхним
и верхним 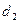 ) из таблицы 3.
) из таблицы 3.
В нашем примере 
Для адаптивную модель Брауна при 9 наблюдениях можно взять в качестве критических табличных уровней величины 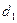 = 1,08 и
= 1,08 и 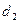 = 1,36.
= 1,36.
Так как рассчитанная величина  , то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
, то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
Для контроля сделанного по  -критерию вывода воспользуемся коэффициентом
-критерию вывода воспользуемся коэффициентом  :
:
 .
.
Т.к. 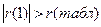 (при
(при  ,
,  ), следовательно, по этому критерию также подтверждается не выполнение свойства независимости уровней остаточной компоненты.
), следовательно, по этому критерию также подтверждается не выполнение свойства независимости уровней остаточной компоненты.
|
|
|
3). Соответствие ряда остатков нормальному закону распределения определим при помощи RS-критерия формула (7):
В нашем примере:  ,
, 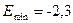 , а размах 2- (-2,3)=4,3.
, а размах 2- (-2,3)=4,3.
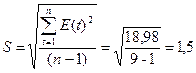 ,
,
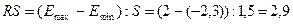 .
.
Значение этого критерия попадает между табулированными границами с заданным уровнем вероятности (для n = 10 и 5%-ного уровня значимости этот интервал равен (2,7-3,7)), следовательно гипотеза о нормальном распределении ряда остатков принимается.
б) Для характеристики точности воспользуемся среднеквадратическим отклонением и средней относительной ошибкой:
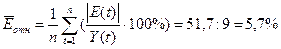
Ее величина 5,7%<10%, что свидетельствует об удовлетворительном уровне точности модели.
3. Для модели регрессии рассчитаем парный коэффициент корреляции переменных, коэффициент эластичности и бета-коэффициент. Прогнозные оценки фактора X(t) на два шага вперед получим на основе среднего прироста от фактически достигнутого уровня.
Оценим величину влияния фактора на исследуемый показатель при помощи коэффициента парной корреляции (результаты вычислений отражены в таблице):
 . (18)
. (18)
Значение коэффициентов парной корреляции лежит в интервале от –1 до +1. Положительное его значение свидетельствует о прямой связи, отрицательное — об обратной, т.е. когда растет одна переменная, другая уменьшается. Чем ближе его значение к единице, тем теснее связь. Считается, что связь до статочно сильная, если коэффициент корреляции по абсолют ной величине превышает 0,7, и слабая, если он меньше 0,3. При равенстве его нулю связь полностью отсутствует.
Таблица 11. Оценка линейного коэффициента корреляции.
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
| r=0 | отсутствует | - |
| 0<r<1 | прямая | С увеличением X увеличивается Y. |
| -1<r<0 | обратная | С увеличением X уменьшается Y, и наоборот |
| r=1 | функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
Таблица 12. По степени тесноты связи различают количественные критерии оценки тесноты связи.
| Величина коэффициента корреляции | Характер связи |
До 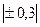
| Практически отсутствует |
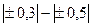
| Слабая |
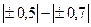
| Умеренная |
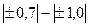
| Сильная |
В нашем случае можно утверждать о сильной прямой зависимости двух исследуемых показателей.
|
|
|
Для расширенной характеристики модели регрессии вычислим несколько дополнительных показателей, первымиз которых является коэффициент детерминации:
 (19)
(19)
Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, более 91% вариации зависимой переменной учтено в модели и обусловлено влиянием включенного фактора.
Учитывая, что коэффициенты регрессии нельзя использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициенты эластичности Э и бета-коэффициент, которые рассчитываются соответственно по формулам:
 (20)
(20)
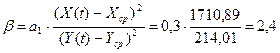 (21)
(21)
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент. Следовательно, при изменении эффективности рынка на один процент эффективность нашей ценной бумаги увеличится на 6,5%.
Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных. С экономической точки зрения он определяет влияние общей ситуации на рынке в целом на судьбу конкретной ценной бумаги. Если его величина положительна, то эффективность ценной бумаги аналогична эффективности рынка. Отрицательная величина бета-коэффициента свидетельствует о снижении эффективности ценной бумаги при повышении эффективности рынка. Этот коэффициент можно рассматривать как количественную меру риска инвестиций в ценные бумаги. При  риск инвестиций выше, чем в среднем по рынку, а при
риск инвестиций выше, чем в среднем по рынку, а при 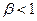 – наоборот.
– наоборот.
В нашем случае бета-коэффициент равен 2,4, т.к.  риск инвестиций выше, чем в среднем по рынку.
риск инвестиций выше, чем в среднем по рынку.
Прогнозные значения 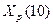 и
и 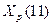 можно определить экспертно или вычислить, на основе экстраполяционных методов. При использовании методов экстраполяции исходят из предположения о сохранении закономерностей прошлого развития на периоде прогнозирования.
можно определить экспертно или вычислить, на основе экстраполяционных методов. При использовании методов экстраполяции исходят из предположения о сохранении закономерностей прошлого развития на периоде прогнозирования.
|
|
|
Простейшим способом прогнозирования является подход от фактически достигнутого уровня 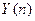 при помощи среднего абсолютного прироста (САП), в соответствии с которым прогноз на
при помощи среднего абсолютного прироста (САП), в соответствии с которым прогноз на 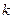 шагов вперед на момент времени
шагов вперед на момент времени 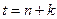 получается по формуле:
получается по формуле:
 , (22)
, (22)
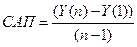 . (23)
. (23)
Этот способ является очень привлекательным из-за простоты и легкости реализации. Однако он имеет несколько существенных недостатков, один из которых состоит в невозможности сформировать интервал, внутрь которого попадет прогнозируемая величина, и указать степень уверенности в этом. В этой связи данный подход используется лишь как начальный ориентир будущего развития или же в условиях очень малого объема наблюдений, когда использовать статистические методы невозможно.
Получим прогнозные оценки фактора на основе величины его среднего абсолютного прироста по соотношению:

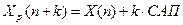
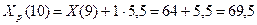

Для получения прогнозных оценок зависимой переменной по модели (17) подставим в нее найденные прогнозные значения фактора:

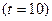 ,
,
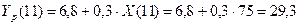
 .
.
Доверительный интервал прогноза будет иметь следующие границы:

Верхняя граница прогноза = 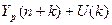
Нижняя граница прогноза = 
Величина  для линейной модели регрессии имеет вид:
для линейной модели регрессии имеет вид:
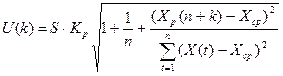 . (24)
. (24)
Для прогноза на два шага имеем:
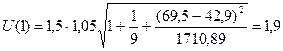 ,
,
 .
.
Результаты вычисления прогнозов представим в таблице 13.
Таблица 13 Прогнозные оценки по модели регрессии.
| Время t | Шаг k | Прогноз Yp(t) | Нижняя граница | Верхняя граница |
| 27,7 | 25,8 | 29,6 | ||
| 29,3 | 27,2 | 31,4 |
|
|
|


