 |
Уравнение Чарномского. Расчет кривых в естественных руслах.
|
|
|
|
Построение кривых свободной поверхности.
.
i0<iк, h0>hкр.
РИСУНОК (лекции прошлый год)
- h>h0 и k>k0, => числитель > 0, и Пк<1 – знаменатель >0. => 
- функция возрастает – глубина возрастает вниз по течению – кривая подпора а1.
- h<h0 и h>hкр, k<k0, => числитель <0, и Пк<1 – знаменатель >0, => 
- глубина потока уменьшается вниз по течению – выпуклая кривая спада b1.
- h<hкр, h<h0, k<k0, Пк>1 –числитель и знаменатель <0, => 
- глубина потока возрастает вниз по течению – вогнутая кривая подпора с1.
i0>iк. h0<hкр
РИСУНОК (лекции прошлый год)
- h>hкр, h>h0 и k>k0, Пк<1 – числитель и знаменатель <0, => - происходит подпор – кривая подпора а2.
- h>h0, h<hкр, k>k0, Пк>1 – числитель >0, знаменатель <0, =>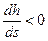 
- глубина уменьшается вниз по течению – кривая спада b2.
- h<h0, k<k0, Пк>1 – числитель и знаменатель <0, => - глубина потока возрастает вниз по течению – кривая подпора с2.
i0=iк,h0=hкр.
РИСУНОК(лекции прошлый год)
- h>h0 и k>k0, Пк<1 – числитель и знаменатель >0, => - глубина возрастает вниз по течению - прямая а3.
- h<hкр, k<k0, Пк>1, => - кривая подпора, с3 –прямая.
2. Типы задач на неравномерное движение.
Первый тип: известны глубины h1 и h2, требуется определить расстояние l между этими сечениями. В зависимости от уклона дна потока l определяется по формулам:
При прямом уклоне: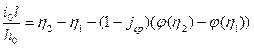 
,
При нулевом уклоне: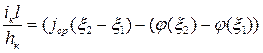 
,
При обратном уклоне: 
. Для определяем 
, 
, 
, 
, 
, 
.
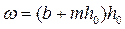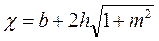Второй тип: известна глубина в одном из сечений (2-2), задано расстояние l между сечениями, необходимо определить глубину в сечении 1-1. решение методом последовательных приближений. Преобразуем: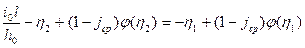 
. Задаваясь произвольными h1, определяем левую часть уравнения. Далее задаваясь величиной η1, определяем φ(η1), подставляем в правую часть, пока уравнение не превратится в тождество. -> h1= η1h0 – первое приближение.
|
|
|
3. Определение длины кривой свободной поверхности потока при неравномерном движении по уравнению Бахметева.
Для русла с положительным уклоном дна: 
, где 
. После преобразования: 
, где 
. Выразим коэффициент Шези по формуле Маннинга, тогда: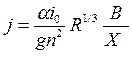 
. Для широких и неглубоких русел В=Х, R=h. 
. При этом дифференциальное уравнение примет вид: 
. После ряда последовательного разделения переменных и интегрирования, получим: .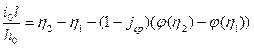
Для дна с горизонтальным руслом дна: равномерного движения не может быть, поэтому нормальная глубина отсутствует. После интегрирования получим: .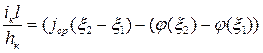
Уравнение Чарномского. Расчет кривых в естественных руслах.
РИСУНОК (стр. 237, Константинов)
Составим уравнение Бернулли для сечений 1—1 и 2—2 относительно
выбранной плоскости сравнения О2—О2,: Э+i0Δl=Э+Δ hf. После приведения: i0Δl = ΔЭ + Δhf.
На участке между сечениями 1—1 и 2—2 движение жидкости является плавноизменяющимся, поэтому энергия потока расходуется на преодоление сопротивлений по длине, а потери энергии на местные сопротивления можно считать пренебрежимо малыми, т. е. Δhf=Δht. Отношение потерь напора к длине участка является средним значением гидравлического уклона на участке:
, тогда 
или 
.
Для непризматических русл с уклонами дна i0=O и i0<0 уравнение 
и 
Уравнения записаны в конечных разностях. В такой форме они впервые были приведены В. И. Чарномским.
При бесконечно малом расстоянии dl между сечениями 1—1 и 2—2 можно получить уравнения в дифференциальной форме: 
, 
, 
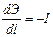5. Гидравлический прыжок. Сущность явления. Структура потока.
Гидравлический прыжок – скачкообразный переход от бурного состояния потока к спокойному, т.е. переход от глубин< критических к глубинам > критических. Глубины перед прыжком и после прыжка называются сопряженными или взаимными глубинами.
|
|
|
РИСУНОК (лекции)
Глубина h’<hкр – меньшая сопряженная глубина, hкр<h” – большая сопряженная глубина. При анализе дифференциального уравнения неравномерного движения жидкости в призматическом русле:
было показано, что функция h=f(l) имеет разрыв.
Для области h<hкр соответствует отношение нормальных глубин к текущей глубине h/h0>1 и параметр кинетичности Пк>1., тогда справедливо неравенство: 
и 1-Пк<1. тогда dh/dl>0 – глубина увеличивается вдоль потока. Если h->hкр возникает гидравлический прыжок.
Рассмотрим изменение удельной энергии сечения потока при пересечении инии критических глубин на участке с горизонтальным руслом. Поток под действием сил трения затормаживается, и глубина изменяется от h<hкр до h”>hкр. Предположим, что такое изменение возможно по кривой подпора плавным переходом. В области увеличения глубин энергия уменьшается за счет потерь на трение. Согласно графику удельная энергия сечения должна возрастать от Эmin до Э”>Экр, что противоречит законам физики. Поэтому отказываемся от возможности плавного перехода: переход от бурного состояния к спокойному в области изменения глубин происходит в виде прыжка. Физически скачок оправдан: на местное сопротивление при резком расширении потока в гидравлическом прыжке затрачивается энергия Эп=Э’-Э”.
6. Типы гидравлических прыжков.
В зависимости от соотношения сопряженных глубин и кинетичности потока прыжок может быть совершенным и волнистым (прыжок-волна).
Прыжок –волна имеет вид ряда затухающих по течению волн с гладкой свободной поверхностью.
РИСУНОК(лекции)
Он возникает при отношении: h”/h’≤2. при этом Пк<3. крутизна волны невелика и частицы линии свободной поверхности не сваливаются под действием собственного веса на транзитный поток.
При совершенном прыжке рост кинетической энергии бурного потока перед прыжком приводит к изменению кинематики потока в верхней части крутой волны: частицы на свободной поверхности значительно теряют скорость и сваливаются навстречу набегающему потоку. Из-за этого гладкая свободная поверхность разрушается, а над транзитным потоком образуется водоворотная область в виде вала. Критерии существования: h”/h’>2
|
|
|
Пк>3.
|
|
|
