Расчет линейного коэффициента парной корреляции

СОДЕРЖАНИЕ

1. Построение линейного уравнения парной регрессии. 3

2. Расчет линейного коэффициента парной корреляции. 6

3. Оценка линейной модели
(коэффициент детерминации и F-критерий Фишера) 7

4. Оценка значимости параметров
уравнения регрессии с помощью t-статистики. 8

5. Точечный прогноз. 10

6. Доверительный интервал прогноза. 11

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.. 12

 

ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

По данным таблицы 1 построить линейное уравнение парной регрессии y=ax+b длины кристалла (у) от продолжительности эксперимента (х). Оценить модель и значимость параметров уравнения регрессии. Получить точечный прогноз у для х =112. Построить доверительный интервал прогноза при уровне значимости α=0,05.

 

Линейная модель парной регрессии имеет вид:

y = ax + b,

где: у – зависимая переменная (результативный признак),
х – независимая (объясняющая) переменная,
a – коэффициент регрессии, показывающий среднее изменение результата при изменении фактора на одну единицу, если единицы измерения исследуемых показателей одинаковы,
b – формальное значение у при х=0.

Построение линейного уравнения парной регрессии

Для решения данной задачи средствами Excel имеются следующие возможности:

А. Непосредственный расчет параметров по известным формулам.

Б. Построение уравнения линейной регрессии с помощью тренда. При этом может быть вычислен коэффициент детерминации.

В. Использование процедуры Регрессия надстройки Анализ данных. В этом случае автоматически вычисляется наиболее полный набор характеристик модели. Возможно проведение анализа регрессионных остатков.

Вариант А

Формулы для расчета параметров a и b получены с помощью метода наименьших квадратов:

,

Где: ; ; ; ; .

Промежуточные расчеты для вычисления параметров a и b приведены в табл. 1.

Таблица 1

Вспомогательные расчеты для определения параметров линейной регрессии

№	Продолжительность эксперимента, X	Длина кристалла, Y	XY	X 2	Y 2	Yx	(Y - Yx)2	(Yx - Yср)2
						21,7	7,5	57,6
						23,0	8,7	40,7
						23,0	3,8	40,7
						24,2	51,3	26,7
						24,2	4,7	26,7
						25,4	0,1	15,7
						25,4	6,9	15,7
						26,6	19,5	7,6
						27,2	4,8	4,6
						27,8	4,9	2,4
						27,8	1,5	2,4
						27,8	27,1	2,4
						28,4	43,6	0,9
						28,4	13,0	0,9
						29,0	1,0	0,1
						29,0	1,0	0,1
						29,0	1,0	0,1
						29,6	1,9	0,1
						29,6	40,9	0,1
						29,6	0,2	0,1
						30,2	33,5	0,8
						30,2	27,2	0,8
						31,4	0,3	4,4
						32,0	3,9	7,3
						32,0	49,4	7,3
						32,6	44,0	10,9
						32,6	0,1	10,9
						33,2	5,0	15,3
						33,8	4,6	20,3
						33,8	0,7	20,3
						35,7	13,4	40,0
						36,3	1,6	48,0
						37,5	0,3	66,3
Сумма:							427,4	498,0
Среднее	112,7	29,3	3431,4	13737,9	888,5	29,3	13,0	15,1

 

Дисперсия факторного признака равна:

Дисперсия результативного признака:

Параметры линейной регрессии:

Вариант Б

С помощью Мастера диаграмм построить точечный график зависимости длина кристалла от продолжительности эксперимента. По полученному графику построить линейный тренд (рис. 1).

Рис. 1. График зависимости длины кристалла от времени эксперимента

Параметры уравнения соответствуют полученным ранее. Коэффициент детерминации 0,5382 говорит о невысокой точности полученной модели – построенное уравнение регрессии объясняет лишь 53,8% обще вариации результативного признака.

Вариант В

Для построения уравнения линейной регрессии следует обратиться к процедуре Регрессия надстройки Анализ данных (Сервис ® Анализ данных ® Регрессия).

Результаты процедуры приведены на рис. 2.

Рис. 2. Результаты процедуры Регрессия

Параметры уравнения регрессии соответствуют полученным ранее. Значение коэффициента регрессии означает, что при увеличении продолжительности эксперимента на одну единицу, длина кристалла увеличится на 0,121 единиц.

Таким образом, зависимость между продолжительностью эксперимента и длиной кристалла имеет вид:

Расчет линейного коэффициента парной корреляции

Уравнение парной линейной регрессии всегда дополняется определением коэффициента линейной корреляции:

Коэффициент линейной корреляции равен:

Полученное значение коэффициента говорит о наличии прямой корреляционной связи между продолжительностью эксперимента и длиной кристалла. Согласно шкале Чеддока, значение 0,7336 свидетельствует о сильной связи между факторами.

3. Оценка линейной модели
(коэффициент детерминации и F-критерий Фишера)

Коэффициент детерминации 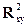равен квадрату коэффициента линейной корреляции и показывает, какая доля дисперсии результативного признака y объясняется изменением факторного признака (отражает качество подбора линейной функции). В данном случае коэффициент детерминации равен:

Это означает, что 53,8% дисперсии результативного признака объясняется изменением факторного признака. Полученное значение говорит о том, что линейная регрессия недостаточно точно описывает зависимость между продолжительностью эксперимента и длиной кристалла.

Оценка значимости уравнения в целом производится обычно с помощью F-критерия Фишера, значение которого вычисляется как

,

где .

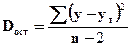Используя коэффициент детерминации, можно вычислить значение F-критерия Фишера по формуле:

.

F-критерий Фишера равен:

Значение F -критерия для степеней свободы k₁ =1 и k₂ =31 и уровня значимости 0,05 (F_крит) равно 4,16 (FРАСПОБР(0,05;1;31). Поскольку F_факт>F_крит (36.122 >4.16), нулевая гипотеза отклоняется, уравнение регрессии на уровне значимости 0,05 признается статистически значимым, а воздействие признака х на у – существенным.

При построении регрессионной модели с помощью процедуры Регрессия рассчитывается Значимость F – вероятность значения F _факт. В данном случае эта величина равна 0. Поскольку рассчитанная значимость F ниже установленного уровня значимости, уравнение регрессии является статистически значимым.

4. Оценка значимости параметров
уравнения регрессии с помощью t-статистики

Параметры a, b и коэффициент корреляции 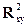были вычислены для одной выборки, для другой выборки из той же генеральной совокупности они будут иметь другие значения, но изменчивость этих значений можно измерить с помощью величины, которая называется стандартной ошибкой. Обозначим стандартные ошибки a, b и коэффициента корреляции 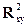соответственно m_a, m_b и m_r. Они вычисляются по формулам:

.

Значения стандартных ошибок рассчитываются автоматически при построении модели с помощью процедуры Регрессия.

Стандартная ошибка для коэффициента регрессии:

Стандартная ошибка для свободного члена:

Стандартная ошибка для коэффициента корреляции:

Оценку статистической значимости параметров a, b уравнения регрессии и коэффициента корреляции 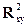проводят с помощью t -статистики Стьюдента и построения доверительных интервалов для каждого из показателей.

Нулевая гипотеза (Н₀) заключается в том, что показатели a, b и 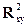незначительно отличаются от нуля, т.е. можно считать a = b = 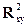=0.

Фактические значения t -статистики Стьюдента определяются по формулам:

T-критерий Стьюдента для коэффициента регрессии:

Критерий Стьюдента для свободного члена:

Критерий Стьюдента для коэффициента корреляции:

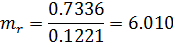
Фактические значения t-статистики Стьюдента сравниваются с критическими. Критическое значение t-статистики для уровня значимости 0,05 и числа степеней свободы 31 равно 2,040. Поскольку все рассчитанные значения t-статистик превышают критическое значение, параметры регрессии являются статистически значимыми.

Построим доверительные интервалы для a – , где , и для b – , где . С вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

Расчет доверительных интервалов для параметров регрессии приведен в табл. 2.

Таблица 2

Расчет доверительных интервалов для параметров регрессии

	a	b	Rxy
Стандартные ошибки	0,0201	2,3600	0,1221
t-статистики (фактические)	6,010	6,649	6,010
t-статистика критическая	2,040	2,040	2,040
Нижняя граница доверительного интервала	0,080	10,879
Верхняя граница доверительного интервала	0,162	20,505

 

Нижняя граница доверительного интервала для параметра a:

Верхняя граница доверительного интервала для параметра a:

Доверительный интервал для параметра b рассчитывается аналогично.

Точечный прогноз

Для получения точечного прогноза необходимо подставить в полученное уравнение регрессии прогнозное значение факторного признака:

Это означает, что при продолжительности эксперимента 112 единиц длина кристалла составит 29,245.

Поделиться:

Воспользуйтесь поиском по сайту: