 |
Лекция 5. Итерационные методы решения уравнений и систем
|
|
|
|
5.1 Простая итерация. Уравнения с одним неизвестным. Пусть задана непрерывная функция f(x) и требуется найти все или некоторые корни уравнения
| f(x)=0. | (5.1.1) |
Эта задача распадается на несколько задач. Во-первых, надо исследовать характер и расположение корней. Во-вторых, найти приближенные значения корней. В-третьих, выбрать из них интересующие нас корни и вычислить их с требуемой точностью.
Первая и вторая задачи решаются аналитическими и графическими методами. Например, многочлен
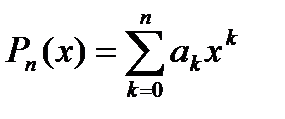
имеет n комплексных корней, не обязательно различных, и все корни лежат внутри круга

Когда ищутся только действительные корни уравнения, то полезно составить таблицу значений f(x). Если в двух соседних узлах таблицы функция имеет разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере один). Если эти узлы близки, то, скорее всего, корень между ними только один. Но выявить по таблице корни четной кратности сложно.
По таблице можно построить график функции y=f(x) и графически найти точки его пересечения с осью абсцисс. Этот способ более нагляден и дает неплохие приближенные значения корней. Во многих задачах такая точность уже достаточна. В технике еще популярны графические методы решения уравнений (номография). Построение графика зачастую позволяет выявить даже корни четной кратности.
Иногда удается заменить уравнение (5.1.1) эквивалентным ему уравнением φ(x) = ψ(x), в котором функции 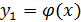 и
и 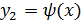 имеют несложные графики. Например, уравнение x sin x – 1 = 0 удобно преобразить к виду sin x = 1/x. Абсциссы точек сечения этих графиков будут корнями исходного уравнения.
имеют несложные графики. Например, уравнение x sin x – 1 = 0 удобно преобразить к виду sin x = 1/x. Абсциссы точек сечения этих графиков будут корнями исходного уравнения.
Дихотомия (деление пополам). Пусть мы нашли такие точки 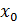 ,
, 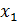 , что
, что 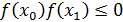 , т.е. на отрезке
, т.е. на отрезке  лежит не менее одного корня уравнения. Найдем середину отрезка
лежит не менее одного корня уравнения. Найдем середину отрезка 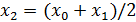 и вычислим
и вычислим 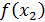 . Из двух половин отрезка выберем ту, для которой
. Из двух половин отрезка выберем ту, для которой  , ибо один из корней лежит на этой половине. Затем новый отрезок опять делим пополам и выберем ту половину, на концах которой функция имеет разные знаки, и т.д. (рис. 5.1).
, ибо один из корней лежит на этой половине. Затем новый отрезок опять делим пополам и выберем ту половину, на концах которой функция имеет разные знаки, и т.д. (рис. 5.1).
|
|
|
Если требуется найти корень с точность ε, то продолжаем деление пополам до тех пор, пока длина отрезка не станет меньше 2ε. Тогда середина последнего отрезка даст значение корня с требуемой точностью.
Дихотомия проста и очень надежна: к простому корню она сходится для любых непрерывных функций f(x), в том числе недифференцируемых; при этом она устойчива к ошибкам округления. Скорость сходимости невелика: за одну итерацию точность увеличивается примерно вдвое, т.е. уточнение трех цифр требует 10 итераций. Зато точность ответа гарантируется.
Перечислим недостатки метода. Для начала расчета надо найти отрезок, на котором функция меняет знак. Если в этом отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс (хотя к одному из них сойдется). Метод неприменим к корням четной кратности. Для корней нечетной высокой кратности он сходится, но менее точен и хуже устойчив к ошибкам округления, возникающим при вычислении f(x). Наконец, на системы уравнений дихотомия не обобщается.
Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна.
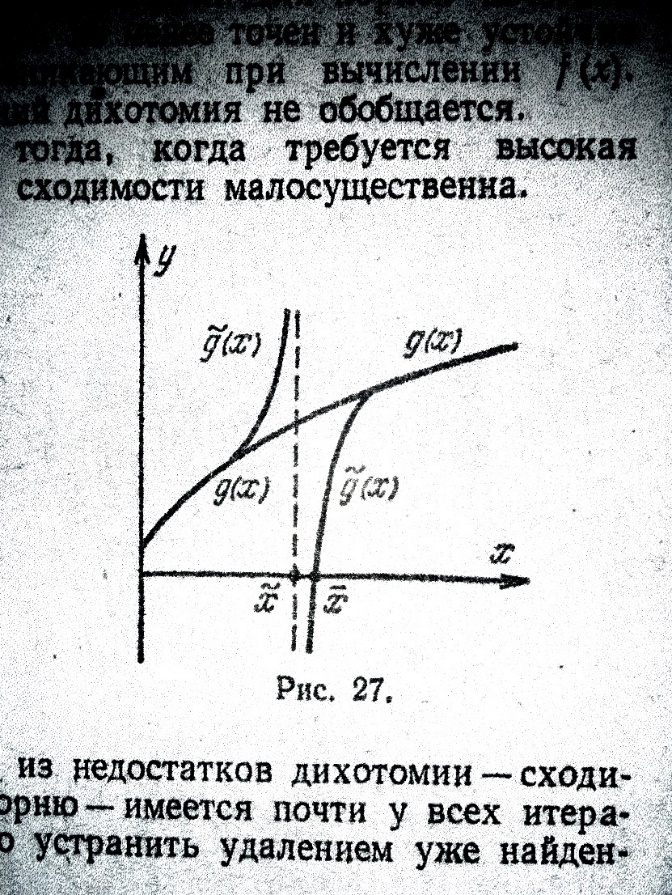
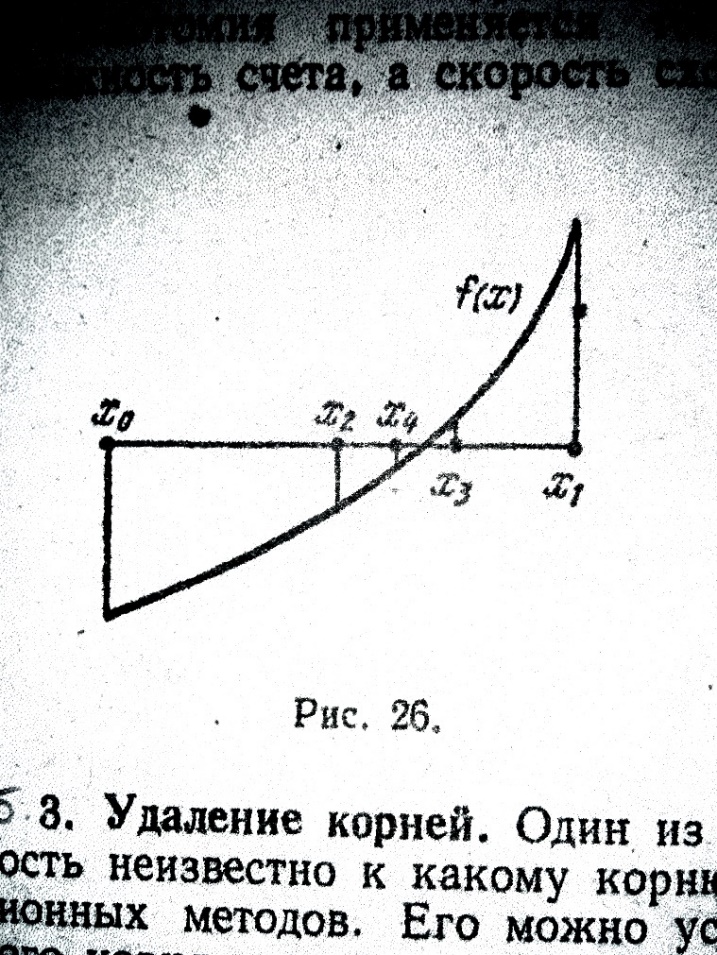
Рис. 5.1. Рис. 5.2.
Удаление корней. Один из недостатков дихотомии – сходимость неизвестно к какому корню – имеется почти у всех итерационных методов. Его можно устранить удалением уже найденного корня.
Если 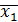 есть простой корень уравнения (5.1.1) и f(x) липшиц-непрерывна, то вспомогательная функция
есть простой корень уравнения (5.1.1) и f(x) липшиц-непрерывна, то вспомогательная функция 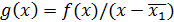 непрерывна, причем все нули функции f(x) и g(x) совпадают, за исключением
непрерывна, причем все нули функции f(x) и g(x) совпадают, за исключением 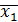 , ибо
, ибо 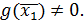 Если
Если 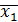 – кратный корень уравнения (5.1.1), то он будет нулем функции
– кратный корень уравнения (5.1.1), то он будет нулем функции 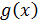 кратности на единицу меньше; остальные нули обеих функций по-прежнему будут одинаковы.
кратности на единицу меньше; остальные нули обеих функций по-прежнему будут одинаковы.
|
|
|
Поэтому найденный корень можно удалить, т.е. перейти к функции 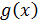 . Тогда нахождение остальных нулей f(x) сведется к нахождению нулей
. Тогда нахождение остальных нулей f(x) сведется к нахождению нулей 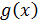 . Когда мы найдем какой-нибудь корень
. Когда мы найдем какой-нибудь корень 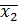 функции
функции 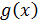 , то этот корень тоже можно удалить, вводя новую вспомогательную функцию
, то этот корень тоже можно удалить, вводя новую вспомогательную функцию 
=  . Так можно последовательно найти все корни f(x).
. Так можно последовательно найти все корни f(x).
Строго говоря, мы находим лишь приближенное значение корня 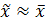 . А функция
. А функция  имеет нуль в точке
имеет нуль в точке 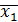 и полюс в близкой к ней точке
и полюс в близкой к ней точке 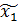 (рис. 5.2); только на некотором расстоянии от этого корня она близка к
(рис. 5.2); только на некотором расстоянии от этого корня она близка к 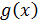 . Чтобы это не сказывалось при нахождении следующих корней, надо вычислять каждый корень с высокой точностью.
. Чтобы это не сказывалось при нахождении следующих корней, надо вычислять каждый корень с высокой точностью.
Кроме того, в любом методе окончательные итерации вблизи определяемого корня рекомендуется делать не по функциям типа 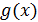 , а по исходной функции
, а по исходной функции 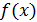 . Последние итерации, вычисленные по функции
. Последние итерации, вычисленные по функции 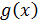 , используются при этом в качестве нулевого приближения. Важно это при нахождении многих корней, ибо чем больше корней удалено, тем меньше нули вспомогательной функции
, используются при этом в качестве нулевого приближения. Важно это при нахождении многих корней, ибо чем больше корней удалено, тем меньше нули вспомогательной функции 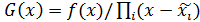 соответствуют остальным нулям функции
соответствуют остальным нулям функции 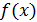 .
.
Учитывая эти предосторожности и вычисляя корни с 8-10 верными десятичными цифрами, зачастую можно определить десятка два корней, о расположении которых заранее ничего не известно (в том числе корней высокой кратности p~5).
Метод простых итераций. Заменим уравнение (5.1.1) эквивалентным ему уравнением  . Это можно сделать многими способами, например, положив
. Это можно сделать многими способами, например, положив  , где
, где  – произвольная непрерывная знакопостоянная функция. Выберем некоторое нулевое приближение
– произвольная непрерывная знакопостоянная функция. Выберем некоторое нулевое приближение 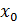 и вычислим дальнейшие приближения по формулам
и вычислим дальнейшие приближения по формулам

| (5.1.2) |
Очевидно, если 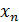 стремится к некоторому пределу
стремится к некоторому пределу 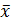 , то этот предел есть корень исходного уравнения.
, то этот предел есть корень исходного уравнения.
Исследуем условия сходимости. Если 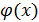 имеет непрерывную производную, тогда
имеет непрерывную производную, тогда
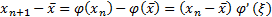 , ,
| (5.1.3) |
где точка ξ лежит между точками 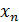 и
и 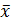 . Поэтому если всюду
. Поэтому если всюду  , то отрезки
, то отрезки  убывают не медленней членов геометрической прогрессии со знаменателем
убывают не медленней членов геометрической прогрессии со знаменателем 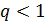 и последовательность
и последовательность 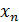 сходится при любом нулевом приближении. Если
сходится при любом нулевом приближении. Если 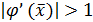 , то в силу непрерывности
, то в силу непрерывности 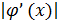 больше единицы и в некоторой окрестности корня; в этом случае итерации не могут сходится. Если
больше единицы и в некоторой окрестности корня; в этом случае итерации не могут сходится. Если 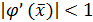 , но вдали от корня
, но вдали от корня 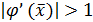 , то итерации сходятся, если нулевое приближение выбрано достаточно близко к корню; при произвольном нулевом приближении сходимости может не быть.
, то итерации сходятся, если нулевое приближение выбрано достаточно близко к корню; при произвольном нулевом приближении сходимости может не быть.
|
|
|
Очевидно, что чем меньше q, тем быстрее сходимость. Вблизи корня асимптотическая сходимость определяется величиной 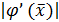 и будет особенно быстрой при
и будет особенно быстрой при 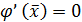 .
.
Значит, успех метода зависит от того, насколько удачно выбрано 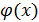 . Например, для извлечения квадратного корня, т.е. решения уравнения
. Например, для извлечения квадратного корня, т.е. решения уравнения 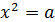 , можно положить
, можно положить 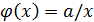 или
или 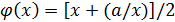 и соответственно написать такие итерационные процессы:
и соответственно написать такие итерационные процессы:
 или или  . .
| (5.1.4) |
Первый процесс вообще не сходится, а второй сходится при любом  ; сходится он очень быстро, ибо
; сходится он очень быстро, ибо 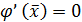 . Второй процесс используют при извлечении корня на калькуляторах.
. Второй процесс используют при извлечении корня на калькуляторах.
Каков практический критерий сходимости, т.е. когда надо прекращать итерации (5.1.2)? Из (5.1.3) видно, что если  , то итерации попеременно оказываются то с одной, то с другой стороны корня, так что корень заключен в интервале
, то итерации попеременно оказываются то с одной, то с другой стороны корня, так что корень заключен в интервале  . Это надежная, хотя несколько грубая оценка. Но она неприменима при
. Это надежная, хотя несколько грубая оценка. Но она неприменима при 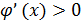 , когда итерации сходятся к корню монотонно, т.е. с одной стороны.
, когда итерации сходятся к корню монотонно, т.е. с одной стороны.
Вблизи корня итерации сходятся примерно, как геометрическая прогрессия со знаменателем 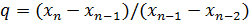 . Чтобы сумма дальнейших ее членов не превосходила ε, должен выполняться критерий сходимости
. Чтобы сумма дальнейших ее членов не превосходила ε, должен выполняться критерий сходимости
 . .
| (5.1.5) |
При выполнении этого условия итерации можно прекращать.
Метод простых итераций и почти все другие итерационные методы имеют важное достоинство: в них не накапливаются ошибки вычислений. Ошибка вычислений эквивалентна некоторому ухудшению очередного приближения. Но это отразится только на числе итераций, а не на точности окончательного результата. Подобные методы устойчивы даже по отношению к грубым ошибкам (компьютерного сбоя), если только ошибка не выбрасывает очередное приближение за пределы области сходимости.
Метод Ньютона. Он называется также методом касательных или методом линеаризации. Если 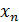 есть некоторое приближение к корню
есть некоторое приближение к корню 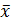 , а
, а 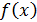 имеет непрерывную производную, то уравнение (5.1.1) можно преобразоватьть следующим образом:
имеет непрерывную производную, то уравнение (5.1.1) можно преобразоватьть следующим образом:
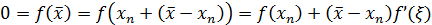 .
.
Приближенно заменяя 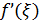 на значение в известной точке
на значение в известной точке 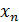 , получим такой итерационный процесс:
, получим такой итерационный процесс:
|
|
|
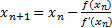 . .
| (5.1.6) |
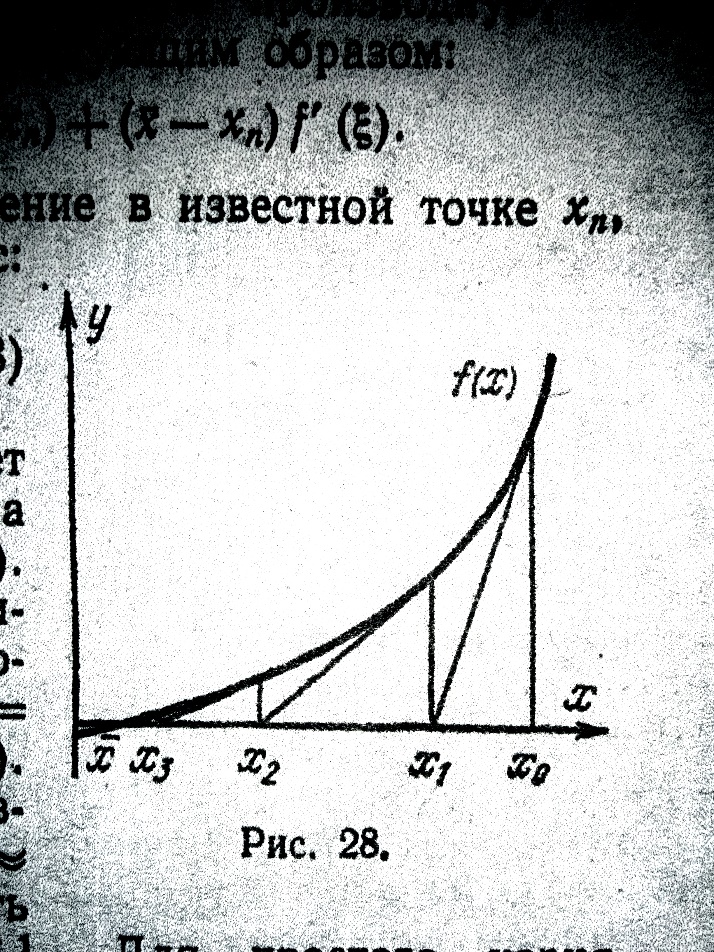 Геометрически этот процесс означает замену на каждой итерации графика
Геометрически этот процесс означает замену на каждой итерации графика 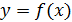 касательной к нему (рис. 28).
касательной к нему (рис. 28).
Метод Ньютона можно рассматривать как частный случай метода простых итераций, если положить  . Тогда
. Тогда 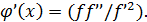 Если
Если 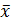 есть р -кратный корень уравнения (5.1.1), то вблизи него
есть р -кратный корень уравнения (5.1.1), то вблизи него 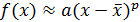 ; отсюда нетрудно получить
; отсюда нетрудно получить  , т.е.
, т.е.  . Для простого корня
. Для простого корня  и
и  . Используя результаты п.4, можно сформулировать следующие условия сходимости итерации (28). Если нулевое приближение выбрано достаточно близко к корню, ньютоновские итерации сходятся; скорость сходимости велика для простого корня и соответствует скорости геометрической прогрессии для кратного корня. При произвольном нулевом приближении итерации сходятся, если всюду
. Используя результаты п.4, можно сформулировать следующие условия сходимости итерации (28). Если нулевое приближение выбрано достаточно близко к корню, ньютоновские итерации сходятся; скорость сходимости велика для простого корня и соответствует скорости геометрической прогрессии для кратного корня. При произвольном нулевом приближении итерации сходятся, если всюду 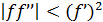 ; в противном случае сходимость будет не при любом нулевом приближении, а только в некоторой окрестности корня.
; в противном случае сходимость будет не при любом нулевом приближении, а только в некоторой окрестности корня.
Сходимость вблизи любого корня монотонна, что легко видеть на рис. 28; но вдали от корня возможна немонотонность итерации. Отметим, что рис. 28 указывает еще на одно достаточное условие сходимости итерации. Пусть 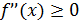 справа от корня на отрезке
справа от корня на отрезке 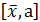 ; если
; если 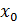 выбрано также справа от корня на этом отрезке, то итерация (28) сходится, причем монотонно. То же будет, если
выбрано также справа от корня на этом отрезке, то итерация (28) сходится, причем монотонно. То же будет, если  слева от корня на отрезке
слева от корня на отрезке 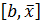 , и на этом же отрезке выбрано нулевое приближение. Таким образом, итерации сходятся к корню с той стороны, с которой
, и на этом же отрезке выбрано нулевое приближение. Таким образом, итерации сходятся к корню с той стороны, с которой 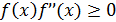 .
.
Оценим скорость сходимости вблизи простого корня. По определению простых итераций,  . Разлагая правую часть по формуле Тейлора и учитывая равенство
. Разлагая правую часть по формуле Тейлора и учитывая равенство  , получим
, получим
 , ,
| (5.1.7) |
| Т а б л и ц а 1 | ||
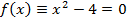
| ||
| n |  ,
метод Ньютона ,
метод Ньютона
|  ,
метод секущих ,
метод секущих
|
| 1,0000 | 1,0000 | |
| 2,5000 | 2,5000 | |
| 2,0500 | 1,8571 | |
| 2,0001 | 1,9836 |
т.е. погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Например, если (n-1) -я итерация давала 3 верных знака, то n-я даст примерно 6 верных знаков, а (n+1) -я – примерно 12 знаков. Это иллюстрирует быструю сходимость вблизи корня. Разумеется, вдали от корня подобные соображения неприменимы.
Если вычисляется корень высокой кратности, то  в знаменателе формулы (28) становится малой вблизи корня. Чтобы не было потери точности, отношение
в знаменателе формулы (28) становится малой вблизи корня. Чтобы не было потери точности, отношение 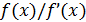 надо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.
надо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.
Для нахождения корней произвольной дифференцируемой функции чаще всего применяют метод Ньютона, особенно если известны разумные начальные приближения для корней.
П р и м е р. Рассмотрим решение уравнения 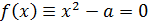 . Тогда общая формула метода Ньютона (5.1.6) принимает вид
. Тогда общая формула метода Ньютона (5.1.6) принимает вид
 .
.
Мы получили вторую формулу (5.1.4), которая, как отмечалось раньше, позволяет очень быстро находить квадратный корень с помощью только сложения и деления. Для иллюстрации в таблице 16 приведен ход итерации при извлечении квадратного корня из а = 4. Видно, что сходимость очень быстрая; несмотря на неважное нулевое приближение, уже третья итерация дает точность 0,005%. Попутно можно заметить, что вблизи корня итерация сходится с одной стороны, т.е. монотонно, хотя первая итерация дает переброс на другую сторону корня.
|
|
|
Метод секущих. В методе Ньютона требуется вычислять производную функции, что не всегда удобно. Можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. Тогда вместо процесса (5.1.6) получим
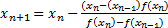 . .
| (5.1.8) |
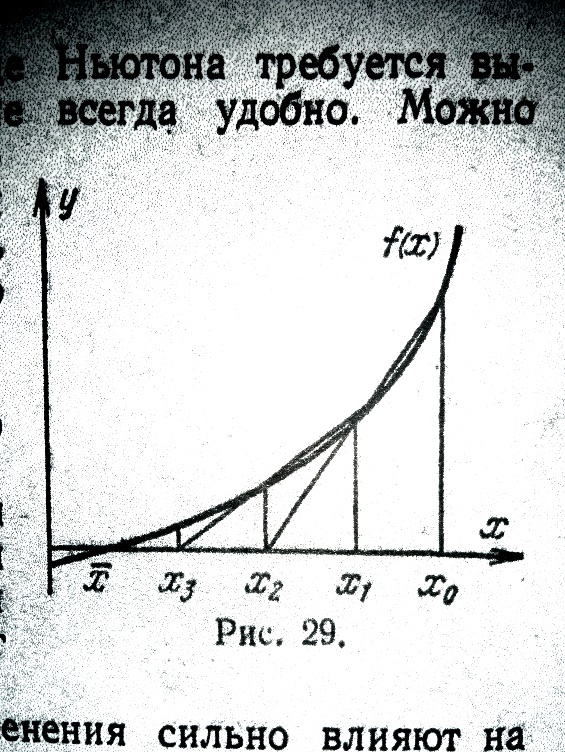 Для начала процесса надо задать
Для начала процесса надо задать 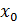 и
и 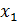 (рис. 29). Такие процессы, где для вычисления очередного приближения надо знать два предыдущих, называют двухшаговыми.
(рис. 29). Такие процессы, где для вычисления очередного приближения надо знать два предыдущих, называют двухшаговыми.
Эти небольшие изменения сильно влияют на характер итераций. Например, сходимость итераций может быть немонотонной не только вдали от корня, но и в малой окрестности корня. Скорость сходимости также изменяется. Приведенный в таблице 1 для сравнения расчет по методу Ньютона показывает, что метод секущих сходится медленнее, т.к. в методе Ньютона ошибка убывает быстрей. Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию.
В знаменателе формулы (5.1.8) стоит разность значений функции; вдали от корня это несущественно, но вблизи корня значения функции малы и очень близки. Возникает потеря значащих цифр, приводящая к «разболтке» счета, что ограничивает точность.
От «разболтки» страхуются так называемым приемом Гарвика. Выбирают не очень малое значение ε, ведут итерации до выполнения условия 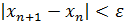 и затем продолжают расчет до тех пор, пока
и затем продолжают расчет до тех пор, пока 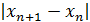 убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчет прекращают и последнюю итерацию не используют.
убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчет прекращают и последнюю итерацию не используют.
Метод парабол. Метод секущих основан на замене функции ф(х) интерполяционным полиномом первой степени по узлам xn, xn-1. По трем последним итерациям можно построить полином второй степени, т.е. заменить график функции параболой. Примем этот полином в форме Ньютона:
P2(x)=f(xn)+(x-xn)f(xn,xn-1) +(x-xn)(x-xn-1)f(xn,xn-1,xn-2).
Приравняв его нулю, получим квадратноеуравнение
az2+bz+c=0, (5.1.9а)
где
z =x - xn, a = f(xn,,xn-1 ,xn-2),
b=a(xn - xn-1)+f(xn,xn-1), c= f(xn). (5.1.9б)
Меньший по модулю из двух корней квадратного уравнения определяет новое приближение xn+1=xn+z.
Для начала расчета надо задать три первых приближения х0,х1,х2 (обычно наугад), т.е. процесс является трехшаговым.
Метод парабол построен по образцу методов третьего порядка, однако замена производных разделенными разностями приводит к существенному уменьшению скорости сходимости.
В этом методе «разболтка» счета вблизи корня сказывается еще больше, чем в методе секущих, т.к. в расчете участвуют вторые разности, но все-таки корни можно найти с хорошей точностью; для определения оптимального числа итераций добно пользоваться приемом Гарвика (см. выше).
Метод парабол исключительно эффективен для нахождения всех корней многочлена высокой степени.
5.2. Итерации для линейных систем уравнений (обычный способ). Итерационные методы решения систем линейных уравнений позволяют получить это решение в виде предела последовательности некоторых векторов, построение которых осуществляется посредством единообразного процесса.
Для определенности запишем систему линейных уравнений четвертого порядка в виде 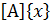 +
+ 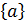 =0, где
=0, где 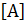 =
= 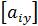 (i,y=1,2,3,4), векторы
(i,y=1,2,3,4), векторы
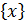 =
= 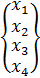 ,
, 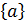 =
= 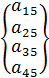 .
.
Разрешим первое из уравнений относительно x 1 , второе – относительно x 2 и т.д. Тогда эту систему можно переписать в виде
x1= α12x2+α13x3+α14x4+α15
x2=α21x1 +α23x3+α24x4+α25
x2=α31x1+α32x2 +α34x4+α35
x2=α41x1+α42x2+α43x3 +α45,(1)
где
 = -
= - 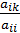 (i=1, 2, 3, 4; k=1, 2, 3, 4, 5). (2)
(i=1, 2, 3, 4; k=1, 2, 3, 4, 5). (2)
Система (1) является частным случаем записи вида
x1=L1(x1, x2, x3, x4)
x2=L2(x1, x2, x3, x4)
x3=L3(x1, x2, x3, x4)
x4=L4(x1, x2, x3, x4). (3)
При этом линейная функция, например, L1(x1, x2, x3, x4) фактически не зависит от x1 согласно (1). Выводы не изменятся, если она будет содержать слагаемое вида α11x1. То же относится к правым частям остальных уравнений.
Зададим произвольные начальные значения неизвестных  ,
, 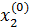 ,
, 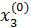 ,
,  . Подставляя эти значения в правые части системы (3), получим первые приближения:
. Подставляя эти значения в правые части системы (3), получим первые приближения:
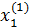 = L1(
= L1(  ,
, 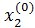 ,
, 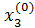 ,
,  ),
),
……………………………..
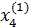 = L4(
= L4(  ,
, 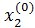 ,
, 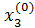 ,
,  ).
).
Полученные первые приближения могут быть таким же образом использованы для получения вторых, третьих и т.д., так что для любого ν можно получить ν -е приближение 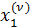 ,
, 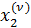 ,
, 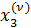 ,
, 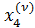 .
.
Можно установить условия, которые обеспечат сходимость получающихся приближений к истинному решению системы x1, x2, x3, x4, для чего достаточно отличия от нуля определителя системы detA≠0.
Обозначим через  ошибку ν -го приближения для k -го неизвестного
ошибку ν -го приближения для k -го неизвестного
 =
= 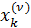 – xk,
– xk,
где xk – точное значение неизвестного в решении системы, которое предполагается существующим.
Показано, что для сходимости итерационного процесса к точному решению системы в этом способе достаточно выполнения условия С<1, где С – некоторое число (верхняя грань сумм коэффициентов (2) системы (1) по столбцам. Эти коэффициенты являются отношениями элементов матрицы коэффициентов исходной системы к диагональным элементам. Следовательно, условие С<1 означает, что все коэффициенты должны быть малы по сравнению с диагональными.
Это условие можно сформулировать и более точно: для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагонадьным элементам, взятым из той же строки, была строго меньше единицы.
Эти выводы можно использовать для оценки погрешности очередного приближения через разность между двумя последовательными значениями k -го неизвестного на соседних итерациях
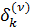 =
= 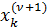 -
- 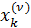 .
.
Для построения вычислительной схемы удобнее находить не непосредственно значения неизвестных, а поправки к предыдущим значениям. За нулевые приближения значений неизвестных в системе (1) можно принять свободные члены соответствующих уравнений:
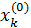 =α k5 (k=1, 2, 3, 4). (10)
=α k5 (k=1, 2, 3, 4). (10)
Пусть 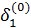 =
= 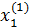 -
-  и вообще
и вообще
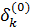 =
= 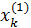 -
- 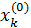 (k=1, 2, 3, 4). (11)
(k=1, 2, 3, 4). (11)
При этом значения 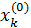 можно считать заданными равенствами (10), а первые приближения
можно считать заданными равенствами (10), а первые приближения 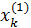 выразить из (1) через
выразить из (1) через 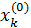 . Вычтя из полученных выражений соответствующие равенства (10), получим поправки к неизвестным первого приближения
. Вычтя из полученных выражений соответствующие равенства (10), получим поправки к неизвестным первого приближения
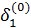 = α12
= α12 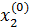 +α13
+α13 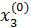 +α14
+α14 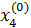
 =α21
=α21  +α23
+α23 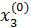 +α24
+α24 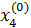
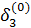 =α31
=α31  +α32
+α32 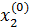 +α34
+α34 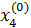
 =α41
=α41  +α42
+α42 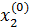 +α43
+α43 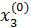 . (12)
. (12)
Равенства (11) можно переписать в виде
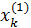 =
= 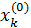 +
+ 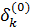 (k=1, 2, 3, 4),
(k=1, 2, 3, 4),
где 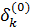 уже определены равенствами (12). Таким же путем можно получить поправки для следующих шагов:
уже определены равенствами (12). Таким же путем можно получить поправки для следующих шагов:
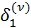 =
=  -
- 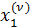 ,
,
откуда
 =
= 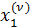 +
+ 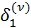 .
.
После несложных преобразований получим выражение для поправки первого неизвестного на ν -й итерации:
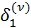 = α12
= α12  +α13
+α13 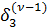 +α14
+α14 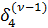 . (13)
. (13)
Аналогичные формулы, позволяющие определять последующие поправки через предыдущие, получаются и для остальных трех неизвестных.
Окончательно для первого неизвестного
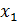 =
=  +
+ 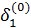 +
+  +
+  …+
…+ 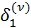 +…,
+…,
аналогично для других неизвестных. Вообще,
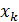 =
= 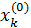 +
+ 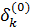 +
+ 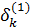 +
+ 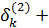 …+
…+ 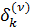 +… (k=1, 2, 3, 4), (14)
+… (k=1, 2, 3, 4), (14)
рекуррентные формулы (14) являются исходными для построения вычислительной схемы в обычной постановке.
5.3. Способ Зейделя. При рассмотрении обычного способа итерации для отыскания очередного приближения значений неизвестных мы пользовались формулами
x1(ν) =L1 (x1(ν-1), x1(ν-1),…),
x2(ν) =L1 (x2(ν-1), x2(ν-1),…), (1)
……………………….
Иначе говоря, следующее приближение полностью определялось значениями, полученными на предыдущем шаге. Между тем уже при построении первого приближения можно, например, вычисляя значение x 2(1) , воспользоваться для x 1 не нулевым приближением x 1(0), а уже полученным нами первым приближением x 1(1) . Вычисляя χ3 , можно использовать уже не только x 1(1), но и x 2(1) и т. д.
Таким образом, вместо формул (1) предлагается использовать для отыскания следующего приближения формулы такого вида (мы снова пишем их для конкретного случая системы четырех уравнений с четырьмя неизвестными):
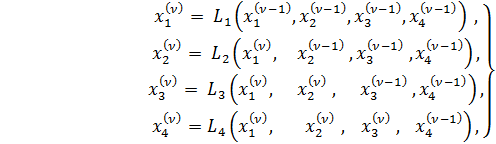 (2)
(2)
Это изменение и составляет идею итераций по способу Зейделя.
Естественно ожидать, что итерации по способу Зейделя дадут при том же числе шагов более точные результаты, чем обычные итерации, или, что то же самое, та же точность будет достигнута за меньшее число шагов. Вообще говоря, эти ожидания оправдываются. Однако нужно иметь в виду, что условия сходимости обычного итерационного процесса и итерационного процесса Зейделя различны. Один из этих процессов для данной системы может оказаться расходящимся тогда, когда другой сходится.
Вычислительная схема итерационного процесса Зейделя строится, как и для обычных итераций, на вычислении последовательных поправок. Рассмотрим эту схему, ограничившись, для краткости, системой трех линейных уравнений с тремя неизвестными. Формулы для отыскания следующих приближений через предыдущие будут в этом случае иметь вид
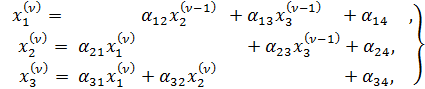 (3)
(3)
Формулы для вычисления поправок легко получить, исходя непосредственно из определения и используя (3). Действительно, для ν-ой итерации
δ1(ν) =  ˗
˗ 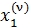 = (
= (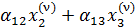 +
+ 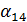 ) ˗ (
) ˗ ( +
+ 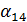 ) = =
) = = 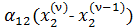 +
+ 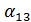 (
( ,
,
так что,
δ1(ν) = 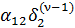 +
+  . (4)
. (4)
Для 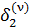 формула выглядит несколько иначе. Так как
формула выглядит несколько иначе. Так как 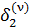 =
= 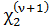 ˗
˗ 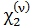 =
=
= (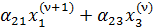 +
+  ) ˗ (
) ˗ ( +
+  ),
),
то
 =
= 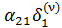 +
+ 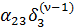 , (5)
, (5)
Аналогично,
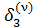 =
=  +
+  . (6)
. (6)
Как и для обычного итерационного процесса, формулы (4)-(6) могут быть использованы для вычисления поправок 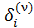 для всех ν = 1, 2, …., но не для ν = 0; для
для всех ν = 1, 2, …., но не для ν = 0; для 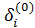 формулы должны быть выведены отдельно. Если принять за начальные приближения значения соответствующих свободных членов
формулы должны быть выведены отдельно. Если принять за начальные приближения значения соответствующих свободных членов
 =
= 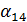 ,
, 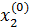 =
= 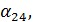
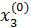 =
= 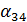 ,
,
то для первых поправок получим выражения
 (7)
(7)
где 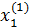 =
=  +
+ 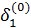 и
и  =
= 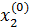 +
+  .
.
Расположение вычислений показано в табл. 1. Верхняя часть ее не отличается от обычного способа, а таблица для вычисления поправок имеет уже несколько другой вид: при вычислении очередных поправок в ряде случаев используются уже полученные поправки того же этапа вычислений. Соответствующие места в табл. 1. подчеркнуты.
Вычисления продолжаются до получения достаточно малых поправок. Окончательные значения неизвестных получаются по формулам
 +… (𝓀 = 1,2,3).
+… (𝓀 = 1,2,3).
Таблица 1. Алгоритм способа Зейделя
для системы трех уравнений с тремя неизвестными
| А |
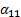
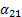
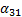
|
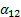
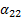
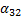
|
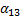
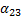

|
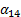

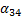
|
| В |
˗
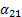
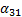
|
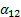 ˗
˗
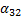
|
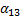
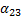 ˗
˗
|
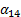

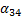
|
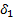
|
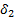
|
| ||
|
|
|


