 |
Соотношение между системными и внесистемными единицами доз
|
|
|
|
| Величина и ее символ | Единица СИ | Внесистемная единица | Соотношение между единицами |
| Экспозиционная доза, X | Кл/кг | Р | 1 Кл/кг = 3.88∙103 Р 1 Р = 2.58∙10–4 Кл/кг |
| Поглощенная доза, D | Гр (Дж/кг) | рад | 1 Гр = 100 рад 1 рад = 0.01 Гр |
| Эквивалентная доза, H | Зв | бэр | 1 Зв = 100 бэр 1 бэр = 0.01 Зв |
| Эффективная доза, E | Зв | Бэр | 1 Зв = 100 бэр 1 бэр = 0.01 Зв |
ПРАКТИЧЕСКАЯ ЧАСТЬ ЗАНЯТИЯ
Типовая задача по расчету прогнозируемого количества радионуклидов после аварийного выброса
В результате аварии на ЧАЭС было выброшено в окружающую среду 8,7×1016 Бк Cs-137. Рассчитайте, какой процент первоначального количества радионуклида остался (распался) на 26.04.2009 г.
Решение: расчет проводится по формуле:
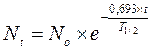 , где:
, где:
N0 – первоначальное количество радиоактивных атомов,
Nt – количество активных атомов спустя время распада t,
T1/2 – период полураспада,
е – основание натурального логарифма.
По условию задачи за время с момента чернобыльской аварии прошло: 2009-1986 = 23 года. Период полураспада Cs-137 – 30 лет. Расчёт начинаем с показателя степени основания натурального логарифма: -0,693×23 г/30 лет = -0,5313; затем рассчитываем e в степени -0,5313, оно равно 0,5874. С учётом этого рассчитываем Nt:
Nt = 8,7×1016 Бк × 0,5874 = 5,11×1016 Бк.
Затем рассчитываем процент оставшегося количества радионуклидов:8,7×1016 – 100 %, а 5,11×1016 – х %, отсюда х=58,74 %. Следовательно, распалось 100–58,74=41,26 %.
Типовая задача по расчету времени, необходимого для достижения объектами заданной окружающей среды активности
Вода после аварии на Чернобыльской АЭС имеет активность по Cs-137 – 30 Бк/л. Рассчитайте время, спустя которое активность воды по Cs-137 не будет превышать РДУ-99.
Решение: расчет проводится по формуле:
|
|
|
 , где:
, где:
А0 – активность продуктов питания и воды,
Аt – активность продуктов питания и воды по РДУ-99,
T1/2 - период полураспада,
ln – натуральный логарифм.
Согласно РДУ-99 активность воды по Cs-137 должна быть не выше 10 Бк/л.
Расчет начинаем с определения величины натурального логарифма: ln 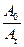 =
= 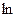
 =1,098. Период полураспада Cs-137 – 30 лет. C учетом этого t=30×1,098/0,693=47,56 года.
=1,098. Период полураспада Cs-137 – 30 лет. C учетом этого t=30×1,098/0,693=47,56 года.
Типовая задача по расчету активности элемента:
Постоянная распада (λ) Тh 1,58×10-18 в сек. Какова активность Тh массой 1 г?
Решение:
Активность источника А – число распадов, происходящих в источнике за единицу времени, Бк, расп/с.
А = λ × N, где
λ – постоянная распада,
N – число не распавшихся радиоактивных ядер в источнике.
Оно находится при помощи числа Авогадро NА и молярной массы М.
N = NА / М = 6,02×1023/223 =26×1020
отсюда
А = (1,58×10-18)×(26×1020)= 4108 Бк.
Также можно узнать поверхностную активность источника Апов – отношение активности (А) к площади (S) его поверхности:
Апов = А / S, (кБк/м2; Ки/км2).
Удельная активность Ауд – отношение активности (А) радиоактивного источника к его массе (m):
Ауд = А / m, (Бк/кг)
Типовая задача:
Определить постоянную распада 131I, если его период полураспада (Т1/2) равен 8,06 суток.
Решение:
Постоянная распада (λ) определяется следующим соотношением:
λ = 0,693 /Т1/2, где
λ - постоянная распада, с-1,
Т 1/2 - период полураспада, отсюда
λ = 0,693 / 8,06 = 0,086 сут-1
Задачи для самостоятельного решения
Задача 1
Изотопы какого элемента образуются из 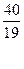 К случае:
К случае:
1) бета-минус; 2) К-захвата? Сколько протонов и нейтронов они содержат?
Задача 2
Ядро какого элемента образуется после пяти последовательных альфа-превращений 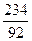 U?
U?
Задача 3
После поглощения нейтрона ядро  U разделилось на два радионуклида:
U разделилось на два радионуклида: 
 Те и
Те и  Zr.
Zr.
Образовавшееся дочернее ядро  Те претерпело четыре последовательных бета-минус распада и превратилось в стабильный изотоп. Какому химическому элементу он принадлежит?
Те претерпело четыре последовательных бета-минус распада и превратилось в стабильный изотоп. Какому химическому элементу он принадлежит?
|
|
|
Задача 4
Постоянная распада  Cs равна 0.023 лет-1. Определить его период полураспада.
Cs равна 0.023 лет-1. Определить его период полураспада.
Задача 5
Определить постоянную распада 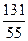 I, если его период полураспада равен 8.06 сут.
I, если его период полураспада равен 8.06 сут.
Задача 6
Определить массу источника 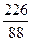 Ra, если его активность равна 3,7×1010 Бк?
Ra, если его активность равна 3,7×1010 Бк?
Задача 7
В изотоп какого элемента превращается  Рu после бета-распада?
Рu после бета-распада?
Задача 8
Определить постоянную распада Сs-137, если его период полураспада (Т1/2) равен 30,1 года.
Тесты для самоконтроля усвоения темы:
1. Заряд ядра равен…
а) числу протонов в ядре;
б) числу нейтронов в ядре;
в) сумме числа протонов и нейтронов в ядре.
|
|
|


