 |
Матричная вязь «золотых скрижалей»
|
|
|
|
Существует в Египте и, по всей видимости, перешедшая оттуда в некоторые другие страны Востока, красивая легенда о том, что мудрые жрецы, обладавшие большими знаниями и заботившиеся о сохранении и передаче этих знаний людям будущего, занесли их на золотые скрижали и хорошо спрятали. Когда же эти знания потребуются людям, они будут им открыты. Сегодня можно констатировать, что легенда эта имеет под собой серьезные основания.
Как уже упоминалось, в начале XX в. археологическая экспедиция под руководством Дж. Квибелла вскрыла в Саккаре (Египет) погребальное сооружение, в котором был захоронен вельможа по имени Хеси-Ра. По печатям, которые находились в склепе, было установлено, что сановник с таким необычным именем жил во времена правления фараона Джосера. Именно в то время, когда началось строительство первой пирамиды [8].
В гробнице находилось 11 деревянных панелей, покрытых с фронтальной поверхности великолепной резьбой, а с тыльной — какими-то (не опубликованными впоследствии) чертежами. Время не пощадило панелей. В склеп попала вода и шесть из них полностью погибли. А из сохранившихся пяти три пострадали очень сильно.
Содержание рельефов, изображенных на панелях, имеет достаточно бытовой характер, как бы повторяющийся и на многих других носителях древности. Отличие в четкости композиции и просматривающемся от панели к панели единстве художественного замысла (рис. 10-13).
Каждая панель включает изображение стоящего сановника, кроме первой, на которой он же представлен сидящим перед столиком с жертвенными хлебцами (?). А это могло свидетельствовать о его жреческом сословии. Небольшие усики, которые полагалось носить архитекторам, показывают, что он является зодчим, а присутствующие на всех панелях письменные принадлежности характеризуют его как писца-вельможу по прутьям-жезлам, которые он держит в руках. Жезлы эти также сопровождают его на всех панелях. Но если малый везде, кроме первой панели, имеет как бы одинаковую длину, то большой, более похожий на прут, чем на жезл, изображен на всех панелях различной длины. Причины этого различия скрыты.
|
|
|
По-видимому, первым обратившим внимание на то, что длины жезлов панели 13 подчинены пропорции 1: √5, что равнозначно соотношению между малой стороной и диагональю прямоугольника ДК со сторонами 1x2, был И. Шевелев. (Как уже отмечалось выше, такой прямоугольник назван И. Шмелевым двусмежным квадратом.) Эти отношения заложены, например, в комплексе гробницы Джосера, в погребальной камере Хеопса и даже в плане города Мемфиса (6,0x12 км), т.е. довольно часто встречаются в различных сооружениях Древнего Египта. Именно диагональ этого прямоугольника можно двумя операциями циркуля разделить на три иррациональные части, кратные золотому числу: 0,618; 0,382; 0,118. Интересно, что это деление И. Шмелев обнаружил на панелях, современная математика его не знала.
Отталкиваясь от этих отношений, И. Шмелев на основе евклидовой геометрии провел анализ структурных элементов всех оставшихся панелей и доказал, приняв за модуль ширину панели, что расстояния между этими элементами описываются величинами, кратными золотым пропорциям [8]. (Замечу, что до этой работы знание золотых пропорций архитекторами пирамид египтология не регистрировала.) Я не буду рассматривать найденные соотношения и повторять проведенные им расчеты. Они частично использовались в работе [9] и тоже частично относятся к размерам измерительных инструментов. Несколько отвлекусь от описания саженей и покажу, что некоторые числовые коэффициенты пропорций между фигурами деревянных панелей имеют величину, равную числам матрицы 3. Выпишу их со схем панелей 10-13, из работы И. Шмелева [8], и сопоставлю с числами в окрестностях главной диагонали матрицы 5 (числа выделены на ней жирным шрифтом):
|
|
|
| 2,618 | 1,309 | 0,944 | 0,618 | 0,250 | 0,146 | 0,073 |
| 2,118 | 1,236 | 0,809 | 0,500 | 0,236 | 0,118 | 0,059 |
| 1,618 | 1,059 | 0,764 | 0,404 | 0,191 | 0,096 | 0,056 |
| 1,528 | 1,00 | 0,654 | 0,382 | 0,154 | 0,090 | 0,034 |
Таким образом, коэффициенты числовых пропорций, получаемые по фигурам деревянных панелей, являются элементами матрицы 5, и по ним можно найти любое число бесконечной матрицы. А это однозначно свидетельствует о том, что Хеси-Ра знал числовые поля матриц 5 и, возможно, 6. Отметив это, вернемся к панелям и попытаемся по коэффициентам жезла и «прутьев» найти их истинные длины. Вероятно, истинные размеры панелей в первоисточниках не приводились, И. Шмелев их не знал и потому не проверил правильность своего пропорционирования. Проведем качественные вычисления, используя принятую И. Шмелевым методику измерения. Поскольку панели египтологи посчитали за так называемые ложные двери1, то их ширина не может быть меньше 1 м и больше 1,30 -1,40 м, т.е. в пределах меньшой сажени. А если это так, то сановник на панели 2 изображен по величине равным своему росту. Известно, что египтяне в древности имели рост где-то 1,75 — 1,85 м. А так как высота панели в два с небольшим раза больше роста сановника, то ее длина находится в пределах 3,5—3,7 м, а ширина в пределах 1,20 м. Этой величине примерно соответствуют половины сажени греческой (230,4 м), великой — 244,0 м и большей — 258,4 м.
_____________________________
1По предположению о «ложных дверях» И.Шмелев посчитал, что все панели имеют одинаковую ширину, а первая только выше других. Но это предположение исходит из евклидовой геометрии. А поскольку египтяне пользовались неевклидовой геометрией, то не только высота, но и ширина первой панели больше других. Это видно из того,- что фигура жреца и его жезл на первой панели меньше, чем на второй. И остальные панели попарно неодинаковы. Но, как будет показано ниже, это не принципиально.

Рис. 10. Панель 1 [8]

Рис. 11. Панель 2[8]

Рис. 12. Панель 3 [8]]

Рис. 13. Панель 4 [8]
Предположим, что панель имеет ширину в полсажени великой, т.е. 122 м, и посмотрим, какую длину имеют жезл и посох на панели 11, используя найденные И. Шмелевым коэффициенты.
|
|
|
Так как длина жезла на панели 2 (рис. И) равна почти половине ширины панели или четверти сажени великой — 61 см, что составляет великий локоть, то наконечник жезла равен:
61 х,1180х 2 = 14,4 см,
а это 1/16 часть греческой сажени:
14,4x16 = 230,4 см.
И, следовательно, наконечник жезла есть пясть сажени греческой. И. Шмелев не придал значения тому, что наконечник жезла имеет выступ в верхней части, который увеличивает его длину в отношении верхней части к нижней примерно на 7/6 Если 6 частей равно 0,118, то 7 частей равны примерно 0,1377, или учетверенной величине последнего члена нисходящего египетского ряда 0,034 х 4 = 0,1378. Умножая 0,1378 на длину жезла, получаем:
61x0,1378=16,81 см.
Верхняя часть наконечника составляет пядь (поллоктя) меньшой сажени. Находим ее:
16,81x8 = 134,5см.
Определим, чему равен черенок жезла:
61 х 0,382 х 2 = 46,6 см, а это локоть церковной сажени:
46,6x4=186,4 см.
Наконец, определим длину посоха:
61 х 2,618 = 159,7 см.
Сановник держит в правой руке посох, длина которого равна кладочной сажени.
Итак, на панели 2 (рис. 11) зашифрованы длины четырех древнерусских саженей: меньшой, кладочной, церковной и греческой.
Обратимся к панели 3 (рис. 12). На ней левая рука сановника сжимает трость с размерами А х (√5 - 1). Найдем ее длину:
61 х(√5 - 1) = 61 х 1,236 = 75,4 см.
И имеем полсажени простой:
75,4x2 = 150,8см.
На панели 4 (рис. 13) у него в руках длинная трость с параметрами:
А х √5 = В.
Определим ее длину:
61 х 2,236 = 136,4 см = В.
Ни одна древнерусская сажень или ее части по длине этому размеру не соответствует. Проверим результат другим способом. Длина диагонали прямоугольника над головой сановника равна В, а В = 5/4 х F. В свою очередь F = 0,882М. По нему и находим F:
F = 0,882 х 122 = 107,6см.
А теперь определяем В:
B = 5/4x107,6 = 134,5см.
И снова получаем самую маленькую древнерусскую сажень — меньшую.
Отмечу, что в этом случае В ≠ А х √5. Некорректность вызвана слабой проработанностью арифметических операций, связанных с золотыми пропорциями (мы, вероятно, плохо понимаем принципы сложения чисел золотых пропорций и получаемые результаты). Но не исключено также, что Хеси-Ра сознательно и логично допустил ряд операций, искажающих результаты расчетов и переход от первой панели к последующим или эти операции мы тоже еще не понимаем, поскольку еще непонятна диспропорция изменения высоты сановника и мерных инструментов при переходе от первой панели к последующим. Какова цель этих искажений и что за ними скрывается, необходимо тщательно исследовать.
|
|
|
Таким образом, изображенные на трех панелях (рис. 11-13) жезлы сановника и трости различной длины имеют размеры, совпадающие с размерами шести древнерусских саженей. Можно полагать, что остальные пять саженей из 11 присутствовали на истлевших панелях. Однако даже найденные панели позволяют утверждать, что при строительстве пирамид использовался комплекс инструментов, соразмерный древнерусским саженям. При этом надо иметь в виду, что, хотя мы и замеряем сажени и их элементы в сантиметрах, они в метричности несоразмерны друг другу и потому складываются по правилам матричной вязи, имея результатом сложения элементы другой сажени.
Это можно показать на примере заполнения матрицы 11, имеющей в своем составе лишь величины полученных саженей. Числа, взятые с панелей, выделены жирным шрифтом, сажени и элементы, найденные по ним, — светлым (матрица 11). Матрице 11 предшествует нисходящий египетский ряд чисел от 1 до 0,0081 (по порядку от первого до одиннадцатого числа матрицы 10), тех самых чисел, которые и определят величину отдельных элементов саженей на главной диагонали.
Главная диагональ матрицы 10 от базисной единицы 1 задает пропорции всем саженям и обусловливает их всеобщее единство, начиная именно с большей сажени 258,4 см и до полвершка меньшой 2,101 см; размер же элементов всех остальных саженей определяется умножением степени обратного золотого числа 0,618 на величину этой сажени. Степень изменяется от 1 до 10 и образует у сажени меньшой, как и у сажени казенной, столбец из семи элементов: полвершка, вершок, полпяди, пядь, поллоктя, локоть, полсажени, сажень. Количество элементов на главной диагонали у остальных саженей по мере приближения к базисной 1 уменьшается, и у двух саженей, кладочной и большей, оказывается равным их длине. Поэтому, по-видимому, не имеет существенного значения, какова по существу ширина деревянных панелей. Ее можно приравнять любой сажени, кроме меньшой, а диагональ пропорционирования в итоге все равно выведет на весь комплекс саженей.
По имеющимся шести саженям остальные легко восстанавливаются, например посредством арифметических операций матричной вязи. Проведем это восстановление. Складываем половину церковного локтя 23,3 см с половиной простой сажени и получаем полсажени царской:
23,3 + 75,4 = 98,7 см.
|
|
|
Царская же сажень равна:
98,7 х 2 = 197,4 см.
Складывая локоть великий с царской саженью, имеем сажень большую:
61,0 + 197,4 = 258,4 см.
Оставшиеся три сажени находятся вычитанием. Вычитаем из сажени церковной сажень простую и получаем локоть малой сажени:
186,4 - 150,8 = 35,6 см.
Умножая его на 4, находим малую сажень:
35,6 x 4 = 142,4 см.
Теперь из греческой сажени вычтем сажень церковную и получаем народный локоть:
230,4 - 186,4 = 44,0 см.
С учетом народного локтя находим народную сажень:
44,0 х 4 = 176,0 см.
И, наконец, вычитаем из греческой сажени народную, получая казенный локоть:
230,4 - 176,0 = 54,4 см.
Откуда казенная сажень равна:
54,4 x 4 = 217,6 см.
Матрица 10
| 0,944 | 0,764 | 0,618 | ||||||||
| 0,892 | 0,721 | 0,584 | 0,382 | |||||||
| 0,842 | 0,681 | 0,551 | 0,236 | |||||||
| 0,520 | 0,146 | |||||||||
| 0,090 | ||||||||||
| 0,056 | ||||||||||
| 0,034 | ||||||||||
| 0,021 | ||||||||||
| 0,013 | ||||||||||
| 0,008 | ||||||||||
Матрица 11
| 258,4 | |||||||||
| 244,0 | 197,4 | 159,7 | |||||||
| 230,4 | 186,4 | 150,8 | 122,0 | 98,7 | |||||
| 217,6 | 176,0 | 142,4 | 115,2 | 93,20 | 75,40 | 61,00 | |||
| 108,8 | 57,60 | 46,60 | 37,70 | ||||||
| 54,40 | 44,00 | 35,60 | 28,80 | 23,30 | |||||
| 27,20 | 14,40 | ||||||||
| 13,60 | 8,90 | ||||||||
| 6,80 | 5,50 | ||||||||
| 3,34 | |||||||||
Итак, на золотых скрижалях, которые, по-видимому, названы И. Шмелевым «золотыми» за большой объем занесенной на них эзотерической информации, жезл и «прутья» в руках Хеси-Ра являются элементами измерительных инструментов, соразмерных с элементами саженей Древней Руси. И можно полагать, что их было не 12, а 14 или 22 (7 х 2 = 14; 11x2 = 22). Тогда размер остальных саженей еще необходимо определить.
Степенное изменение числовых величин от большей сажени по главной диагонали к меньшой обусловливает уникальное арифметическое пропорционирование, по которому каждый член пропорции, являясь элементом большей сажени по диагонали, становится и элементом другой сажени, другой пропорции по вертикали. То есть выполняет две как бы смежные функции и может перейти на другую форму пропорционирования, стать элементом третьей сажени (и не только третьей) посредством матричной вязи. Результатом сложения, например, двух иррациональных чисел становится третье, им пропорциональное, иррациональное число. К такому же результату приводят операции умножения и деления элементов саженей как друг на друга, так и на члены главной диагонали матрицы 11. Всеобщая комбинаторика матричной вязи древних саженей обладает качественно иными свойствами, чем метричностъ, резко уменьшая объемы измерений и вычислений в проектировании и в строительстве, заключая в себе золотые пропорции, а вместе с ними и соответствие соизмерителъных инструментов природным структурам.
ПОНЯТИЕ О ЖИВЫХ ФИГУРАХ
Информация о том, что числа и геометрические фигуры делятся на живые и неживые, время от времени появляется в разнообразной эзотерической литературе. Общим недостатком этой информации является отсутствие однозначных критериев отличия живых чисел и фигур от аналогичных, но неживых. Какое качество, а может быть, какие качества способны придавать таким абстрактным понятиям, как число и геометрическая фигура, свойства, признаваемые за живыми и неживыми телами, в этих публикациях не сообщается. Но все же за этой информацией скрывается истинность, до поры нам не известная. Ниже я изложу свое понимание живого и неживого соотношения между фигурами-абстракциями, а сначала остановлюсь подробнее на статье «Серебряное сечение» А. Чернова [18], по-видимому, одной из последних попыток связать золотое сечение с живыми фигурами (живым квадратом) посредством введения понятия «серебряное сечение» как отображение связи золотого числа Ф с числом π.
Начну с определения понятия «серебряное сечение» в [18]: «серебряное сечение - это когда целое относится к меньшему отрезку как длина окружности к ее диаметру».
Это очень красивое определение, напоминающее определение понятия «золотая пропорция», страдает по меньшей мере двумя недостатками: во-первых, длина окружности, которая неявным образом вводится как понятие «целое», не является целым, т.е. большим отрезком, частью которого является «меньший» отрезок — диаметр; во-вторых, они качественно несопоставимы по своим функциям (диаметр — всегда перпендикуляр к окружности), а потому несоразмерны, что и отражает их трансцендентное частное π.
К тому же, вышеприведенное определение есть трансформация более известной истины «отношение длины одной окружности к ее диаметру всегда равно отношению длины другой окружности к своему диаметру». Пропорции тут не получается, да и решение у этого отношения единственное (?), а не восемь, как у золотой пропорции.
И все же, не обращая внимания на эту неточность, следует отдать должное оригинальности подхода автора к проблеме, привлечению в качестве аргументации разнообразного, достаточно доказательного, материала — от «Слова о полку Игореве» и стихотворений А.С.Пушкина до семицветия И.Ньютона и плана церкви Успения XII века в Старой Ладоге. Последний является основным и определяющим аргументом автора в доказательстве существования живого квадрата и серебряной пропорции. Поскольку на плане церкви Успения нанесены, как считает А. Чернов, размеры восьми саженей, являющихся исходной точкой в аргументации автора, посмотрим, какие можно сделать выводы из анализа

Рис. 14. План церкви Успения в Старой Ладоге. Мерный ангел живого квадрата на плане церкви Успения [18]предлагаемого плана.
Автор полагает, что древний зодчий нанес на план размеры восьми единственных эталонных (статичных) саженей, которыми пользовались новгородцы (напомню, что у Б.А. Рыбакова таких и тоже единственных саженей семь), и сопровождает план 'вычислениями с точностью до миллиметров (которыми новгородцы не пользовались), доказывающими знание зодчими чисел π и Ф. Приведу для наглядности эти вычисления:
«КсВ — косая великая сажень — 2,484 м (диагональ квадрата со стороною МХ).
СБ — сажень большая — 2,157 м (рост человека (?) с поднятой рукой).
КН — косая новгородская по трости 2,005 м (уменьшенная на 4 мм диагональ квадрата со стороной ТК).
МХ — маховая, она же мерная — 1,756 м (размах рук). РС — ростовая сажень - 1,705 м. ТС - темная сажень - 1,589 м (диагональ полуквадрата со стороной ТК). ТК — тмутараканс-кая, она же малая — 1,421 м (два шага (?) или от основания шеи до земли (?). (Знак вопроса поставлен мной — А. Ч.)
КсЧВЕ и ТНОК — квадраты;
АГВЕ — живой квадрат
АГ: РС = 2Ф: π = 1,03...
Если 4: π = √5: МХ, то МХ = π √5: 4,
(2МХ + КН): МХ = π.
Отношение парных саженей:
МХ: ТК = √5 - 1; СБ: РС = Ф2: π 2 + 1; 2);
КсВ: КН = √2: (π - 2); СЧ: ТС = √5 - 1.
Эти вычисления легко производить, оперируя метрическими размерами саженей и используя знания современных вычислительных методов. Если же вспомнить, что метричность в XII в. отсутствовала и зодчий тех времен никогда ничего не измерял и тем более арифметически не делил (самые просвещенные умели делить табличными методами целые числа на целые), оперируя целыми отрезками саженей, величиной до вершка, то все построения автора становятся сомнительными. Вершки для проведения проделанных выше расчетов совершенно не подходят. Однако метод, который применяет зодчий, практически повторяет построение рассмотренных выше «вавилонов» Б. А. Рыбакова.
Следует отметить, что важнейшим аргументом автора в доказательстве существования живого квадрата является наличие на схеме линии АГ, уменьшающей длину стороны КсЕ квадрата КсЧВЕ примерно на 3%. Эти 3% и составляют разницу между длиной маховой сажени и ростовой сажени. На них же в среднем отличается размах рук человека от его роста. И именно они, по мнению автора, способствуют образованию живого квадрата АГВЕ. Но какова роль живого квадрата на этой схеме? И для чего он вообще предназначался, как и вся схема? Остается неясным.
Я полагаю, что перед нами наглядное пособие. Разбивочный чертеж, выполненный применительно к некоторым саженям или их элементам, который демонстрировал ученикам зодчего простейший способ перехода от симметричной прямоугольной формы к асимметричной косоугольной посредством применения прямоугольных треугольников. Об этом говорит линия СГ, которая, если следовать логике автора, должна быть девятой саженью, но является элементом прямого угла БГС. Об этом свидетельствует прямая БГ, которую можно было бы посчитать за половину сажени. Об этом свидетельствует смещение на плане конструктивных элементов относительно общепринятого центра симметрии СБ.
Фигура ангела является не только некоторым эталоном построения саженей, но и как бы показывает, что асимметричное построение плана не нарушает соразмерности всего сооружения и даже облагораживает его.
И вот здесь-то встает вопрос: Зачем зодчему портить красивое симметричное сооружение приданием ему асимметричной формы? Чего он добивался асимметрией? И что поразительно, не он один.
А.Чернов правильно отметил, что КсЧВЕ является квадратом, а АГВЕ — живым квадратом (ниже это будет рассмотрено подробнее), но не придал значения тому, что, вводя асимметрию между квадратом и живым квадратом (правая стена храма сдвинута относительно левой именно на их разницу), зодчий дополнительно превращал внутренний объем церкви из холодного неподвижного (неживого) в теплое живое. Он вводил в неподвижные конструкции элемент движения человеческого восприятия (и не только зрительного), тем самым оживляя и усиливая их.
Человек, находящийся в любой точке внутри такой конструкции, не замечает асимметрии, она как бы растворяется в объеме, но чувствует, созерцая помещение, некоторое движение объема, его постоянное изменение, как бы дыхание. И это полуинтуитивное воздействие успокаивает его, создает душевный уют и тем приближает его к Богу.
Что касается саженей, то на плане отображены, с точностью до полвершка, т.е. практически без нарушения соразмерности, две группы саженей. Запишем их в сопоставлении с саженями из матрицы 2 (первая строка сопоставления):
| 2,176; | 1,76; | 1,442; | 2,440; | 1,974; | 1,597; |
| 2,157; | 1,756; | 1,421; | 2,484; | 2,005; | 1,589; |
| 1,963. |
Совпадение для соразмерных, но несоизмеримых безэталонных, инструментов просто поразительное. Разница только в двух случаях превышает 2 см. И только одна ростовая сажень выпадает из этого ряда. Если же взять вершок маховой сажени 0,055 м и отнять от сажени народной 1,76 м, то получим точный размер так называемой ростовой сажени 1,705 м. Не так ли была получена данная сажень? Или это снова очередное совпадение?
Но вернемся к живым фигурам. Проведем на листе линию 1 и попросим несколько человек определить ее длину без применения измерительного инструмента (рис. 15).
В зависимости от тренированности человека ошибка в определении длины в среднем будет находиться в пределах 1,5-10%. Проведем недалеко от нее другую линию примерно на 3-5% длиннее первой и попросим тех же людей определить, которая из линий длиннее. Большинство правильно определят линию большей длины, хотя могут оказаться и такие, для которых линии будут иметь одинаковые длины.

Рис.15. К определению длин
Теперь можно, изменив фон, окружающий линию 2 (например, множеством параллельных штрихов вокруг нее), создать впечатление, что ее длина изменилась, и количество ошибок при определении большей длины возрастет. И хотя собственная длина линий не изменилась, большинство из созерцающих будут констатировать кажущееся изменение длины той из них, у которой меняется окружающий фон.
Таким образом неподвижные линии постоянной длины становятся как бы движущимися, изменяющими на изменяющемся фоне свою длину, и изменение это будет четко фиксироваться в пределах 1,5-4,5% от их длины. А это, вероятно, и есть те параметры, которые характеризуют живые фигуры и которые неоднократно встречаются в строительных композициях.
Исходя из этих соображений попробую дать определение живому квадрату: Живой квадрат — это та переходная граница, которая отделяет восприятие квадрата от прямоугольника. Точнее, это такая фигура, которая еще не квадрат, но и, уже не прямоугольник. Живой квадрат имеет как бы подвижные грани, движение, а следовательно, живет. Живое - это, подвижное. Неживое — неизменное, статичное. Живое - это процесс. А процесс символизируют древние сажени. Вот мы снова вернулись к ним. Тем более, что ранее было опущено рассмотрение раздвоения саженей на 6 частей, тогда как в старину чаще делили на 7. Чем же было вызвано нарушение традиций?
Возьмем, например, ту же казенную сажень и разложим поэлементно: сажень — 217,6см, полсажени — 108,8см, локоть — 54,4см, пядь — 27, 2 см, полпяди — 13, 6 см, вершок — 6,8 см. Все. Сложим их за исключением сажени:
108,8 + 54,4 + 27,2 + 13,6 + 6,8 = 210,8 см.
Для получения полной длины сажени не хватает ровно одного вершка. А вершок это 1/32 часть сажени:
6,8: 217,6 х 100 = 3,125%.
Таким образом, длина вершка составляет 3,125% от длины сажени. Округленно те же самые 3%, которые образуют живой квадрат церкви Успения и на которые размах рук человека больше его высоты. Случайно ли это совпадение или перед нами «потаенный» седьмой вершок? Вершок, свидетельствующий, что сажень есть процесс, а не инструмент для измерения. И не потому ли, что он составляет 3% сажени, на нем заканчивается раздвоение саженей?
Но, возможно, иное. Добавление к сажени вершка приводит к такому ее наращиванию, которое зрительно воспринимается как начало изменения длины сажени. Добавление второго вершка фиксируется уже как переход сажени к другому размеру. Отсюда можно предположить, что изменение длины сажени в сторону увеличения или уменьшения на полвершка не оказывает существенного влияния на ее соразмерность другим саженям и в то же время становится началом изменения стандарта сажени или фигуры. Это обстоятельство позволяло древним строителям работать с деревянными саженями, концы которых очень быстро истираются. Да и на плане церкви Успения, быть может, отложены именно «поработавшие» сажени, а более вероятно — сумма вершков различных саженей.
По предположению А.А. Пилецкого [10], вершок является модулем зрительного отличия самой сажени от ее интуитивно воспринимаемой длины. Модулем соблюдения соразмерности инструментов, расплывчатой границей перехода неживой фигуры в живую.
Здесь к месту привести еще одну из особенностей применения на Руси древних саженей. Разбивку объекта с их помощью проводили так, что длина замерялась одной саженью, ширина — другой, высота — третьей, внутренняя планировка — четвертой. И каждый размер вмещал в себя целое число саженей или их элементов. Чем обусловливалась такая методика и что она обеспечивала, пока неизвестно. Но в качестве некоторого намека на объяснение можно рассмотреть соразмерность двух прямоугольных треугольников: ранее построенного золотого треугольника с фиксированными сторонами а = 1,272; б = 1,618; с = 2,057 и священного египетского треугольника со сторонами а' = 3; б' = 4; с' = 5.
Какие обстоятельства способствовали освящению треугольника 3:4:5, неизвестно тоже, но на интуитивном уровне чувствуется, что между ними есть какая-то противоположная общность, какая то-связь, обусловливающая некоторый антагонизм в существовании холодных чисел золотого треугольника и веселых, теплых чисел священного.
Еще раз вернемся к матрице А.А. Пилецкого. Она записана в форме, определяющей взаимосвязь системы саженей и их элементов. Но, как показано в [19], основой этой матрицы является русская матрица, построенная на системе восходящих и нисходящих ветвей золотого ряда. Приведу фрагмент русской матрицы (матрица 12).
Отмечу, что центр фрагмента матрицы 12 занимает базисная единица 1 (т.е. число, качественно отличающееся от всех других чисел матрицы), а по диагонали от нее слева направо снизу вверх идет восходящая ветвь золотой пропорции. По той же диагонали от базисной единица 1 вниз идет нисходящий ряд той же пропорции. Диагональ, проходящая через базисную единицу 1 слева направо снизу вверх, называется главной диагональю. По вертикали вверх от базисной единица 1 ряд чисел удваивается, а вниз раздваивается. Это свойство матрицы и отображает принцип разделения древних саженей на элементы.
Обратим внимание на то, что главная диагональ пересекает вертикальный ряд чисел под углом 45°, образуя вместе с другой диагональю, вертикальным и горизонтальным рядами фигуру двойного креста (выделен на матрице 12 серым цветом). Базисная же единица 1, является, по-видимому, отправной величиной, например в древнеегипетском каноне. Числа 10, 100, 1000,...,91, 991, 9991,... становятся для них базисными, т.е. качественно отличными от других «рядовых» иррациональных чисел в тех структурах, в которых они проявляются. Первая цифра по главной диагонали вверх от базисной единицы в = Ф — золотое число. Числа a и с на этой диагонали отсутствуют. Однако, как показано выше, они связаны с числом Ф пропорцией:
а6 = b3 = Ф3 = с2
(см. раздел «Элементы золотых пропорций) и потому являются элементами одной последовательности, не входящей в ряд главной диагонали. Эта последовательность и становится, видимо, эталоном измерения параметров геометрической фигуры (в данном случае золотого треугольника), не изменяющей внутренних пропорций элементов при степенном изменении каждого параметра. Другими словами, каждый параметр золотого треугольника есть величина, образованная каким-то одним, общим для всех, статичным числом — эталоном. И длина каждого параметра по модулю
равна эталону, возведенному в некоторую степень. Например, параметры золотого треугольника могут быть образованы числом-эталоном 1,04929.... Тогда 1.0495 = 1,272 — один катет треугольника, 1,04910 = 1,618 — другой катет и 1,04915 = 2,058 — его гипотенуза.
Матрица 12
| 15,11 | 12,22 | 9,888 | 8,000 | 6,472 | 5,236 | 4,236 |
| 7,554 | 6,111 | 4,944 | 4,000 | 3,236 | 2,618 | 2,118 |
| 3,777 | 3,056 | 2,472 | 2,000 | 1,618 | 1,309 | 1,059 |
| 1,888 | 1,528 | 1,236 | 1,000 | 0,809 | 0,654 | 0,529 |
| 0,944 | 0,764 | 0,618 | 0,500 | 0,404 | 0,327 | 0,264 |
| 0,472 | 0,382 | 0,309 | 0,250 | 0,202 | 0,164 | 0,132 |
| 0,236 | 0,191 | 0,154 | 0,125 | 0,101 | 0,082 | 0,066 |
Таким образом, основным отличием неживых фигур от живых становится соразмерность образующих их параметров какому-то неявному эталонному рациональному или иррациональному размеру. «Живой» является такая фигура, параметры которой несоразмерны никаким явным или скрытым эталонам.
Учитывая данное обстоятельство, сопоставим в абсолютных значениях, насколько и в чем отличаются друг от друга золотой и священный египетский треугольники, приведя сначала к единому базису модуль их малого катета. Для этого все модули сторон разделим на величину их малого катета:
| Золотой треугольник | Египетский священный треугольник |
| а = 1; | a1 = 1; |
| b = 1,272...; | b1 = 1,333...; |
| c = 1,618 | с1 =1,666... |
Приведение к единому размеру египетского треугольника показывает, что его больший катет и гипотенуза представляют бесконечную рациональную дробь, округленную до целых чисел: 3,9999... = 4, 4,99199... = 5. Такие же стороны золотого треугольника тоже представляют бесконечную, но иррациональную дробь. Стороны этих двух треугольников имеют между собой некоторое математическое родство. Но если в золотом треугольнике между модулями большого катета и гипотенузой имеется степенная зависимость, то в египетском такая зависимость отсутствует, а следовательно, отсутствует и единый степенной эталон измерения параметров каждой из сторон. Определим, насколько отличаются синусы углов α 1 и α:
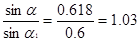
Оказывается, что синусы углов данных треугольников различаются на те же 3%, на которые отличается живой квадрат от неживого, но в меньшую сторону для египетского треугольника. А это и есть свидетельство его принадлежности живым фигурам.
И хотя египетский живой (и, по-видимому, поэтому священный) треугольник образуется умножением всех сторон треугольника авс на 3 и округлением до целых чисел, соразмерных метру, эти операции не отражаются на пропорциях его сторон и не приводят к появлению эталонного размера.
Между тем использование в проектировании фигур стандартного метра в качестве единого измерительного инструмента для определения начальных параметров объектов способствует неявному появлению в этих параметрах эталонных размеров, а следовательно, и превращения образованных ими фигур, а вместе с ними и будущих объектов, в неживые, вредные для проживания людей объекты. Нельзя исключить также, что эталонные размеры образуются не только как степенные величины, но и как интегрированные единичные элементы длины. Видимо, по этой причине древние зодчие и проектировали различные параметры сооружений каждый своей мерой — саженью, поскольку, как было показано ранее, сажени несовместимы ни с каким эталоном длины. А потому при соизмерениях саженями никогда не образуют ни явных, ни неявных эталонных величин. И надо согласиться с А.Черновым [18]: «Метр — гениальное изобретение, но он годится только для измерения уже найденных пропорций. Не больше!». И добавить:
Проектировать и строить на основе метра нельзя!
ЛОГИКА ДРЕВНИХ САЖЕНЕЙ
Выше упоминалось, что в Древней Руси имело хождение множество соизмерительных инструментов — саженей. Вот уже почти два столетия ученые пытаются привести это множество к минимальному количеству типоразмеров и пока безуспешно. И эти неудачи не случайны. Во всех работах по системам мер сажени рассматриваются только как измерительные инструменты, имеющие строго определенную длину и единственный способ применения — измерение. По сформулированной за два столетия метром логике измерительный инструмент должен с большой точностью делиться на некоторое количество одинаковых мерных единиц, обычно кратных «круглому числу». Например, метр делится на 10 дециметров, дециметр делится на 10 сантиметров и т.д. Сам по себе метр является стандартной величиной, десятимиллионной долей от одной четверти парижского меридиана, и получение его эталонной длины — достаточно сложная, продолжительная и дорогостоящая операция. А потому раз полученный эталонный отрезок в виде выверенного платинового стержня уже почти 200 лет хранится в футляре при постоянной температуре, давлении и влажности. И даже в этих условиях требуется уточнение его длины.
Возникают вопросы: А какими же методами производилось хранение измерительных инструментов в древности? Имеет ли смысл говорить об их точности? И не является ли требование точного измерения длины саженей логическим отголоском привычного использования стандартной единицы длины — метра? Ведь «хранение» это длилось тысячи лет со времен Древнего Египта, если не ранее [19]. К тому же никаких эталонов не найдено. Требовать от таких инструментов точности при отсутствии даже намеков на эталоны не приходится. И тем не менее...
Сооружения как Древней Руси, так и Древнего Египта своей соразмерностью, пропорциональностью и эстетической красотой, предназначенностью для облагораживающего воздействия на людей намного превосходят типовые и не типовые «коробки» XIX и XX вв. — детища очень точного стандартного метра.
Эта соразмерность и эстетическая красота сооружений — следствие особой, подвижной функции взаимосвязанного комплекса древнерусских саженей, заключающаяся в том, что их основное назначение — соизмерение, а потому они — не статические линейки, а остановленные длиною продолжающиеся


