 |
Исследование выборочных статистических данных
|
|
|
|
Объем продаж компьютерной техники в магазине «Горбушкин двор» изменяется в зависимости от времени года, ассортимента товаров, цен производителя и т.д. Известны статистические данные этого показателя в течение некоторого времени.
1) Необходимо сгруппировать данные, образовав 8-10 интервалов. Найти распределение частот и относительных частот.
2) Найти и построить эмпирическую функцию распределения
Найдем эмпирическую функцию распределения по формуле:
3) Построить полигон распределения. Построить гистограмму частот и относительных частот распределения. Объяснить основное свойство гистограммы
4) Выдвинуть гипотезу о вероятном распределении показателя. Найти точечные оценки числовых характеристик распределения
5) Методом моментов найти оценку параметров распределения, считая его равномерным на заданном интервале значений
6) Оценить истинные значения параметров выборочного распределения с помощью доверительного интервала с надежностью 0.95,считая распределение нормальным
7) Использовать критерий Пирсона, при уровне значимости 0.05 проверить согласуется ли гипотеза о
а) нормальном распределении выборки
б) показательном распределении выборки
в) равномерном распределении выборки
1. Сгруппировав данные получим 8 интервалов:
| [3;5) | [5;7) | [7;9) | [9;11) | [11;13) | [13;15) | [15;17) | [17;19] |
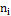
| 1 | 1 | 4 | 9 | 17 | 12 | 4 | 1 |
Найдем распределение частот:
| 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
|
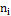
| 1 | 1 | 4 | 9 | 17 | 12 | 4 | 1 |
Найдем распределение относительных частот
n= 1+1+4+9+17+12+4+1=49
|
| 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 0.02 | 0.02 | 0.08 | 0.18 | 0.35 | 0.24 | 0.082 | 0.02 |
2.
1. x 
(- 
0
2. x 
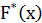=0.02
3. x 
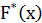=0.02+0.02=0.04
4. x 
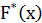=0.04+0.08=0.12
5. x 
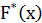=0.12+0.18=0.3
6. x 
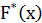=0.3+0.35=0.65
|
|
|
7. x 
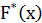=0.65+0.24=0.89
8. x 
0.89+0.082=0.972
9. x 
0.97+0.02=1
Итак, эмпирическая функция распределения будет выглядеть так
Построим эмпирическую функцию распределения
3.
Полигон распределения
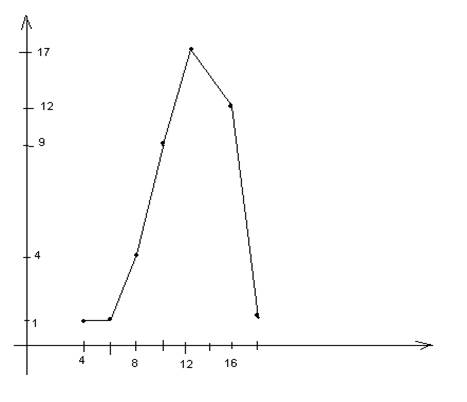
Гистограммой – называется фигура состоящая из прямоугольника. Основания прямоугольников – интервальные задания случайной величины, высота прямоугольников
- для гистограммы частот находится по формуле:
= 
=0.5
=0.5
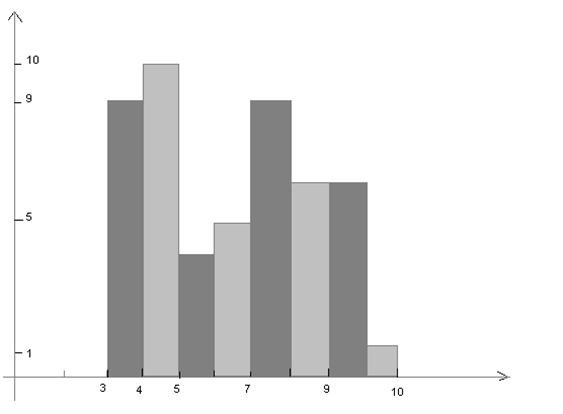
- для гистограммы относительных частот находится по формуле:
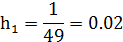
4. 
.
5. Метод моментов применяется для оценки неизвестных параметров распределения, суть методов заключается в том, что приравниваются теоретические и эмпирические моменты. Если закон распределения содержит 1 параметр, то для оценки этого параметра составляется одно уравнение, в котором теоретический момент приравнивают к эмпирическому моменту. Если распределение случайной величины содержит 2 параметра, то составляют два уравнения и т.д.
Считая распределение равномерным на заданном интервале значений запишем дифференциальный закон:
2 параметра распределения a и b 
M(x)= 
D(x)= 
D(x) 
(4+6+32+90+204+168+64+18)= 
=11.959
= 
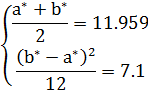
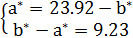
6. Доверительным называют интервал который с заданной надежностью 
показывает заданный параметр.
Истинное значение измеряемой величины равно ее математическому ожиданию a. Поэтому задача сводится к оценке математического ожидания (при известном 
) при помощи доверительного интервала
= 2.009
Все величины кроме S(среднеквадратического отклонения) известны. Для нахождения S сначала найдем 
(исправленную дисперсию).
*175.4=3.58
=1.89
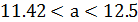
7. а) 1. 
2. Вычислим теоретические частоты, учитывая, что n=49, h=1, 
=2.6, по формуле:
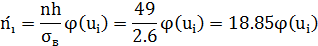
| i |
| 
| 
| 
|
| 1 | 4 | -3,06 | 0.0037 | 0,07 |
| 2 | 6 | -2,29 | 0.0290 | 0,55 |
| 3 | 8 | -1,52 | 0.1257 | 2,37 |
| 4 | 10 | -0,75 | 0.3011 | 5,67 |
| 5 | 12 | 0,015 | 0.3989 | 7,52 |
| 6 | 14 | 0,78 | 0.2943 | 5,55 |
| 7 | 16 | 1,55 | 0.1200 | 2,26 |
| 8 | 18 | 2,32 | 0.0270 | 0,51 |
|
|
|
3. Сравним эмпирические и теоретические частоты
I) составим расчетную таблицу, из которой найдем наблюдаемое значение критерия
|
| 
| 
| 
| 
|
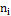
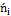
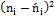
| 1 | 1 | 0,07 | 0,93 | 0,86 | 12,2 |
| 2 | 1 | 0,55 | 0,45 | 0,2 | 0,36 |
| 3 | 4 | 2,37 | 1,63 | 2,66 | 1,12 |
| 4 | 9 | 5,67 | 3,33 | 11,09 | 1,95 |
| 5 | 17 | 7,52 | 9,48 | 89,87 | 11,95 |
| 6 | 12 | 5.55 | 6,45 | 61,15 | 11,02 |
| 7 | 4 | 2,26 | 1,74 | 3,03 | 1,1 |
| 8 | 1 | 0,51 | 0,49 | 0,24 | 0,47 |
Из таблицы найдем 
II) по таблице критических точек распределения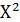 
, по уровню значимости 
k=s-3=8-3=5
Т.к. 
- гипотезу о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические и теоретические частоты различаются значимо.
Б)
|
|
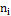
| 3-5 | 1 |
| 5-7 | 1 |
| 7-9 | 4 |
| 9-11 | 9 |
| 11-13 | 17 |
| 13-15 | 12 |
| 15-17 | 4 |
| 17-19 | 1 |
1. 
2. Найдем оценку параметра предполагаемого показательного распределения
Т.о. плотность предполагаемого показательного распределения имеет вид:
(x>0)
3. Найдем вероятности попадания X в каждый из интервалов по формуле:
Например, для первого интервала:
⅀=0.89
4. 
, где 
-й интервал
Например, для первого интервала
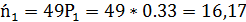
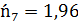
5. Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого составим расчетную таблицу, причем объединим малочисленные частоты (4+6=10), (16+18=34) и соответствующие им теоретические частоты (16,17+5,88=22,05), (1,96+1,96=3,92)
|
|
|
|
|
|
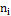
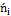
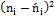
| 1 | 2 | 21,07 | -19,07 | 363,6 | 17,2 |
| 2 | 4 | 3,92 | -0,08 | 0,0064 | 0,0016 |
| 3 | 9 | 3,43 | 5,57 | 31,02 | 9,04 |
| 4 | 17 | 3,136 | 13,864 | 192,2 | 61,3 |
| 5 | 12 | 2,744 | 9,26 | 85,74 | 31,25 |
| 6 | 5 | 3,92 | 1,08 | 1,166 | 0,3 |
| 49 |
По таблице найдем 
Т.к.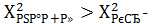 
гипотеза о распределении X по показательному закону отвергается.
в)
|
|
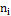
| 3-7 | 2 |
| 7-9 | 4 |
| 9-11 | 9 |
| 11-13 | 17 |
| 13-15 | 12 |
| 15-19 | 5 |
1. 
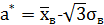
2. 
3. Найдем теоретические частоты:
4. Сравним эмпирические и теоретические частоты, используя критерий Пирсона приняв число степеней свободы k=s-3=8-3=5 для этого
Составим расчетную таблицу
|
|
|
|
|
|
|
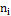
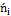
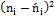
| 1 | 2 | 2,91 | -0,91 | 0,83 | 0,28 |
| 2 | 4 | 10,78 | -6,78 | 45,96 | 4,27 |
| 3 | 9 | 10,78 | -1,78 | 3,17 | 0,294 |
| 4 | 17 | 10,78 | 6,22 | 38,7 | 3,6 |
| 5 | 12 | 10,78 | 1,22 | 1,49 | 0,14 |
| 6 | 5 | 7,87 | -2,87 | 8,24 | 1,04 |
| ⅀ | 50 | 9,62 |
Из расчетной таблицы получаем 
Найдем по таблице критических точек распределения 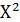по уровню значимости 
критическую точку правосторонней критической области 
|
|
|
Т.к. 
гипотеза о равномерном распределении отвергается.
Корреляция величин
Корреляция величин
Корреляция — зависимость между случайными величинами, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной зависимости корреляции, как правило, рассматривается тогда, когда одна из величин зависит не только от данной другой, но и от ряда случайных факторов. Зависимость между двумя случайными событиями проявляется в том, что условная вероятность одного из них при наступлении другого отличается от безусловной вероятности. Аналогично, влияние одной случайной величины на другую характеризуется условными распределениями одной из них при фиксированных значениях другой.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Задача
Совместный закон распределения суммы дивидендов, выплачиваемых по привилегированной и обыкновенной акциям некоторой компании, задается следующей таблицей
|
|
| ||
| 0 | 1 | 2 | |
| 2 | 
| 
| 
|
| 4 | 
| 
| 
|
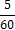
1) Построить маргинальные законы распределения случайных величин X и Y.
) = 
)= 
Проверка: 
| Y | 0 | 1 | 2 |
| p |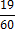 
| 
| 
|
X: 
)= 
)= 
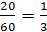
Проверка: 
| X | 2 | 4 |
| p | 
| 
|
2) Вычислить числовые характеристики: математические ожидания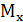 
и 
, дисперсии 
и 
, среднеквадратические отклонения 
и 
|
|
|
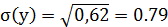
3) Условные вероятности составляющих X и Y соответственно вычисляются по соответствующим формулам:
P(
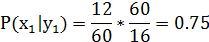
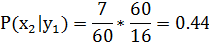
| X | 2 | 4 |
| 0,75 | 0.44 |
| X | 0 | 1 | 2 |
| 0.3 | 0.325 | 0.375 |
4) Вычислить числовые характеристики: условное математическое ожидание 
, дисперсию 
и среднее квадратическое отклонение 
Условным математическим ожиданием дискретной случайной величины Y при X=x (x – определенное возможное значение X) называется произведение всех возможных значение y на их условные вероятности.
Условная дисперсия:
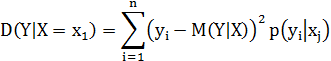
Условное среднеквадратическое значение:
5) Рассчитать коэффициенты корреляции 
и сделать выводы о линейной зависимости случайных величин X и Y.
Коэффициент корреляции находится по формуле:
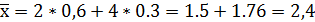
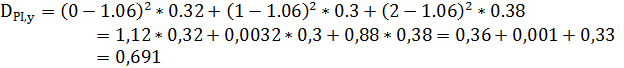
связь знакоположительная
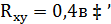связь средняя умеренная
Заключение
В своей работе я постаралась наиболее кратким и наиболее понятным языком выразить основные положения и понятия о теории вероятности, математической статистике и случайных процессах.
В курсовой работе я изучила непрерывные случайные величины, исследование методами математической статистики и корреляцию величин.
Благодаря этой курсовой работе я многому научилась, узнала что многие очевидные для нас вещи основаны на теории вероятности и математической статистике.
В последнее время методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.
С помощью изучения экономических показателей мы можем понять происходящее в экономике. Они отражают текущее или будущее состояние экономики и могут помочь распознать приближение как положительных, так и отрицательных изменений в бизнесе и личных финансах.
Список использованной литературы
1. В.Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике»
2. В.Е.Гмурман «Теория вероятностей и математическая статистика»
3. Булинский, А. В., Ширяев, А. Н. «Теория случайных процессов»
4. В.С.Кривошеева, С.Н.Поздеева «Методические указания и задания к курсовой работе по дисциплине «Теория вероятностей и математическая статистика»»
5. http://www.aup.ru/books/m155/4_13.htm
6. http://www.ecscada.ru/files/documents/agtu/fpe/Din7.doc
7. http://ru.wikipedia.org/wiki
|
|
|
12 |
