 |
Обобщенный метод наименьших квадратов (ОМНК)
|
|
|
|
Понятие обобщенной линейной регрессионной модели (ОЛРМ)
При моделировании экономических процессов некоторые предпосылки относительно возмущений, сделанные в классической регрессионной модели, являются нереальными. Чаще всего нарушаются условия взаимной некоррелированности и гомоскедастичности возмущений, которые представляются в виде:
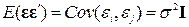 . (1)
. (1)
Эти условия оправданы в тех случаях, когда наблюдаемые объекты однородны и описывающие их величины не зависят от своих собственных значений, относящихся к прошлому времени).
Модели регрессии, для которых не выполнено условие (1), называются обобщенными линейными регрессионными моделями (ОЛРМ) (в отличие отклассической линейной регрессионной модели (КЛРМ)).
Пусть W – некоторая симметричная положительно определенная матрица порядка n ´ n[1]. И пусть ковариационная матрица возмущений (S e) выражается через W соотношением: S e = se2 W.
Предполагается, что число se2 неизвестно, а матрица W известна.
Обобщенная линейная регрессионная модель описывается следующей системой соотношений:
1) Y = Xb + e,
2) E(e) = 0,
3) E(ee ¢) = Se = se2 W,
4) х1,х2, …, xp – переменные, не являющиеся случайными, так что для каждой их них Cov (xi, ei) = 0 " i,
5) rang(X) = p + 1 < n,
где n – количество наблюдений,
р – количество независимых переменных,
se2 – дисперсия возмущений (неизвестный параметр),
W - известная матрица, которая может быть недиагональной и с различными по величине элементами на главной диагонали.
оценивание параметров bj обобщенной линейной регрессионной модели методом наименьших квадратов приведет к следующему:
1) оценки bj не будут обладать свойством эффективности (хотя останутся несмещенными и состоятельными);
|
|
|
2) se2 – оценка дисперсии возмущений является смещенной;
3) ковариационная матрица оценок Var(B) = se2(X¢X)-1 является смещенным оценщиком истинной ковариационной матрицы. Это означает, что t-статистики окажутся искаженными, и будет получено неправильное представление о статистической надежности результатов оценивания уравнения регрессии.
Таким образом, обобщенная модель линейной регрессии отличается от классической отказом от требования некоррелированности и гомоскедастичности возмущения и не может быть корректно оценена методом наименьших квадратов.
Что можно сделать в случае невыполнения предпосылок?
1. Попытаться изменить спецификацию модели, чтобы устранить автокорреляцию или гетероскедастичность возмущений (например, ввести еще объясняющие переменные).
2. Выбрать такой метод оценивания параметров модели, который при нарушении рассматриваемых предпосылок мог бы максимально обеспечить требуемые свойства полученных оценок, например, метод Эйткена.
Обобщенный метод наименьших квадратов (ОМНК)
Задача оценивания параметров обобщенной линейной регрессионной модели может быть решена с помощью так называемого обобщенного метода наименьших квадратов (ОМНК), или метода Эйткена, в соответствии с которым оценки, найденные с помощью оценщика
 , (2)
, (2)
являются несмещенными линейными оценками параметров b, обладающими наименьшей дисперсией и матрицей ковариаций[2]:
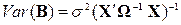 . (3)
. (3)
Таким образом, при использовании ОМНК исходят из того, что ковариационная матрица возмущений известна, хотя и с точностью до неизвестного постоянного множителя s2, несмещенную оценку которого мы строить умеем.
Чтобы убедиться в эффективности оценок параметров модели, которые получены обобщенным методом наименьших квадратов, воспользуемся знанием матрицы W для того, чтобы преобразовать исходные данные
|
|
|
 ,
, 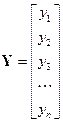
к виду, соответствующему требованиям классической модели. Это значит, что после выполненного преобразования исходных данных возмущения e пр должны удовлетворять свойствам гомоскедастичности и взаимной некоррелированности, т.е. матрица ковариаций должна иметь вид:
S e пр = s2 I.
Выполнить необходимые преобразования позволяет известный результат из матричной алгебры, в соответствии с которым всякая невырожденная симметричная матрица А допускает представление в виде:
А = РР¢,
где Р – невырожденная матрица (т.е. определитель этой матрицы отличен от нуля).
Поскольку приняли, что W – невырожденная симметричная матрица, то считаем, что существует такая невырожденная матрица Р (n´n), что
W = РР ¢. (4)
Умножив (4) слева на Р-1, а справа – на (Р¢) -1, получим:
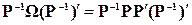 ,
,
 ,
,
 . (5)
. (5)
Если же к (4) применить правило обращения произведения квадратных матриц: (АВ) -1 = В-1 А-1, то получим:
W -1 = (РР ¢) -1,
W -1 = (Р ¢) -1 Р-1,
W -1 = (Р -1) ¢ Р -1. (6)
Теперь вернемся к ОЛРМ: Y = Xb + e, и умножив это уравнение слева на матрицу Р-1, получим:
Р-1Y = Р-1Xb + Р-1e,
или
Yпр = Xпр b + eпр, (7)
 |
где Yпр = Р-1Y,
Xпр = Р-1X, (8)
eпр = Р-1e
Нетрудно проверить, что модель (7) удовлетворяет всем требованиям классической регрессии. Для этого достаточно убедиться в том, что
S e пр = Е(eпр eпр¢) = s2 I.
Действительно,
 .
.
Применив к преобразованным данным МНК, получим формулу (2) – оператор оценивания для обобщенного метода наименьших квадратов:

Итак, эффективной оценкой (наилучшей в классе всех линейных (относительно Y) несмещенных оценок) параметра b будет оценка
 ,
,
или
 ,
,
ковариационная матрица которой определяется формулой:
 ,
,
или
 .
.
Таким образом, можно найти такое преобразование первоначальных переменных Х и Y, которое приведет матрицу ковариаций возмущений обобщенной линейной регрессионной модели Е(e e¢) к виду s2 I, т.е. можно применить к этим преобразованным данным обычный МНК. В этом и состоит суть метода Эйткена со вспомогательной моделью:
1) преобразование обобщенной модели во вспомогательную, удовлетворяющую предпосылкам МНК, по схеме:
Yпр = Р -1Y, Xпр = Р -1X;
|
|
|
2) применение ко вспомогательной модели метода наименьших квадратов. Полученные оценки будут равнозначны оценкам Эйткена для параметров обобщенной модели регрессии.
Определим вид матрицы  , которая используется для преобразования исходных данных.
, которая используется для преобразования исходных данных.
ковариационная матрица возмущений линейной регрессионной модели



на главной диагонали содержит дисперсии возмущений различных наблюдений, а внедиагональные элементы представляют их ковариации.
В зависимости от выполнения рассматриваемых основных предпосылок классической регрессии ковариационная матрица имеет тот или иной вид:
· при гомоскедастичности (постоянстве дисперсий случайной компоненты) и отсутствии автокорреляции (взаимной некоррелированности возмущений)

· при гетероскедастичности и отсутствии автокорреляции возмущений ковариационная матрица возмущений по-прежнему диагональная (т.е. все внедиагональные элементы равны нулю), но с различными по величине диагональными элементами (дисперсиями):
 .
.
При этом, учитывая, что Se = se2 W, можем записать:
 .
.
Ранее приняли W = РР ¢, поэтому W -1 = (Р -1) ¢ Р -1 = С¢С.
 .
.
Таким образом, в условиях невыполнения предпосылки о гомоскедастичности возмущений, но при отсутствии автокорреляции имеем:
 ;
;
Соответствующие преобразованные исходные данные имеют при такой матрице преобразования Р-1 следующий вид:
 ;
; 
· при автокоррелированности и гомоскедастичности возмущений матрица ковариаций не может быть диагональной, поскольку в ситуациях, когда исходные наблюдения регистрируются во времени, возмущения оказываются взаимозависимыми, коррелированными.
Естественным допущением относительно природы зависимости регрессионных остатков является гипотеза, в соответствии с которой эта зависимость ослабевает по мере их взаимного удаления друг от друга во времени. Одной из удобных форм реализации этого допущения (при сохранении свойства гомоскедастичности остатков) является следующая:
|
|
|
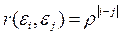 , (9)
, (9)
где  – коэффициент корреляции между
– коэффициент корреляции между  и
и 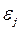 , а
, а  – некоторое число, по модулю меньшее единицы. очевидно, из (9) следует, что по своему вероятностному смыслу
– некоторое число, по модулю меньшее единицы. очевидно, из (9) следует, что по своему вероятностному смыслу  – это коэффициент корреляции между соседними по времени остатками, так как
– это коэффициент корреляции между соседними по времени остатками, так как
 .
.
При  (т.е. при неограниченном удалении остатков друг от друга во времени) величина
(т.е. при неограниченном удалении остатков друг от друга во времени) величина  стремится к нулю, (связь исчезает).
стремится к нулю, (связь исчезает).
Ковариация остатков равна:
 .
.
Действительно,
 ,
,
где 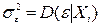 – условная дисперсия остатков (не зависящая от величины Хi в силу гомоскедастичности). Так что ковариационная матрица остатков имеет в данном случае вид:
– условная дисперсия остатков (не зависящая от величины Хi в силу гомоскедастичности). Так что ковариационная матрица остатков имеет в данном случае вид:
 .
.
Таким образом, при автокорреляции (первого порядка)
 .
.
Тогда
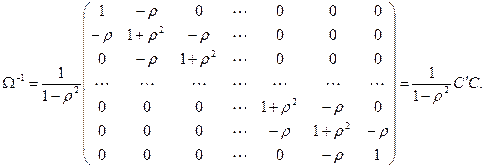

Соответствующие преобразованные исходные данные имеют при такой матрице преобразования Р-1 следующий вид:
 ;
;

Рассмотрим дальше более подробно 2 типа распространенных в практике эконометрического исследования обобщенных моделей регрессии:
· линейная модель регрессии с гетероскедастичными возмущениями;
· линейная модель регрессии с автокоррелированными возмущениями.
[1] Симметричная матрица – квадратная матрица, у которой a ij = a ji " i,j.
Положительно определенная матрица – матрица, у которой главные миноры положительны.
[2] Модель ОМЛР иногда специфицируется в виде: Y = Xb + e, причем E(e) = 0, E(ee ¢) = V, где V – известная симметричная положительно определенная матрица. Различие с выше описанным состоит в замене se2 W на V. Здесь,.
|
|
|


