 |
Оценка основных финансовых активов
|
|
|
|
Главным свойством активов является их способность приносить доход. Предприятие не будет инвестировать свои ресурсы в приобретение имущества, которое не обладает таким свойством. Сумма будущих чистых денежных притоков (NPV), которые актив способен обеспечить предприятию, называется его внутренней (справедливой или экономической) стоимостью. Определение внутренней стоимости активов, предназначенных для производственного использования, производится в ходе инвестиционного проектирования. На этой стадии предприятие сопоставляет расходы по приобретению и переработке активов с прогнозируемой величиной будущих доходов (чистых денежных притоков), которые могут быть получены от использования этих активов. Для дисконтирования будущих денежных притоков используется процентная ставка, отражающая альтернативную стоимость привлекаемого предприятием капитала. Очевидно, что способность производственных активов приносить доход определяется прежде всего их потребительскими (физическими) свойствами – качеством материалов, производительностью оборудования и т.п. Успех любого инвестиционного проекта в большой мере зависит от того, насколько верно инженерно-технические службы предприятия оценили именно эти свойства активов, а производственные и коммерческие подразделения смогли их полностью реализовать.
Вместе с тем предприятие может располагать активами, не обладающими никакими потребительскими свойствами, кроме одного – способности приносить доход. Речь идет о финансовых активах – вложениях в ценные бумаги, банковские депозиты и других инвестициях, целью которых является получение текущего дохода (проценты, дивиденды, купоны) или увеличение их первоначальной стоимости. Внутренняя стоимость этих активов определяется таким же образом, как и любых других: путем расчета их NPV. Различие состоит в том, что для определения внутренней стоимости финансовых активов не требуется предварительное выполнение каких-то специальных инженерно-технических обоснований, учитывающих их потребительские или физические свойства. Единственное, что нужно знать для оценки такого актива это величину и временную структуру обеспечиваемых им денежных потоков. Выполнив дисконтирование этих потоков по ставке, отражающей альтернативные издержки предприятия по привлекаемому им капиталу, можно определить внутреннюю стоимость (NPV) данного актива.
|
|
|
Финансовые активы отражают инвестиции предприятия в собственные и заемные капиталы других компаний. Однако и само предприятие может выпустить (эмитировать) и продать соответствующие ценные бумаги. В этом случае они уже не будут являться для него финансовыми активами, а станут частью собственного (акции) или заемного (облигации) капитала. Зато для покупателей этих ценных бумаг они будут финансовыми активами. Предприятие-эмитент само определяет размер и временную структуру выплат дохода по выпускаемым им ценным бумагам. При этом оно пользуется теми же самыми правилами расчета их внутренней стоимости, что и при покупке. Оно понимает, что именно по этим правилам будет оценивать эмитируемые бумаги рынок. Поэтому условия размещаемых ценных бумаг должны быть такими, чтобы заинтересовать потенциальных инвесторов. в то же время предприятие должно исходить из своих реальных финансовых возможностей, так как выплата чрезмерно высоких доходов может стать для него непосильным бременем.
Рассмотрим методику оценки рынком основных финансовых активов: акций и облигаций. Обычно считается, что оценка финансовых инструментов – это прежде всего сфера деятельности спекулянтов на фондовых биржах, имеющая мало общего с деятельностью коммерческих предприятий нефинансового характера. Подтверждением такого мнения служат большое число видов различных ценных бумаг, специфика торговли ими, наличие специального биржевого законодательства. Не вступая в дискуссию по поводу данной точки зрения, отметим, что значительная часть обращающихся на фондовом рынке бумаг – это свидетельства о праве их владельцев на долю собственности в конкретных предприятиях или подтверждения займов, предоставленных предприятиям. Иными словами на фондовом рынке покупаются и продаются элементы правой части баланса предприятий – собственного капитала и пассивов. То, что для держателя ценной бумаги является финансовым активом, для эмитировавшего эту бумагу предприятия означает обязательство возврата долга или выплаты дивидендов. Очевидно, что эмитент заинтересован в росте рыночной стоимости своих ценных бумаг: при их первичном размещении он получит больше денег в свое распоряжение; в процессе вторичных торгов увеличение рыночной стоимости его капитала и долгосрочных обязательств является свидетельством хорошей работы предприятия и роста стоимости его активов. Инвестор заинтересован в приобретении бумаг с высокой внутренней стоимостью, однако заплатить за них он хотел бы поменьше. В общем виде его задача сводится к поиску инструментов, неверно (с его точки зрения) оцененных рынком. Если инструмент недооценен рынком (рыночная цена ниже внутренний стоимости), инвестор захочет его купить. В противном случае (завышенной рыночной оценки) владелец постарается продать переоцененный рынком инструмент.
|
|
|
Важнейшим вопросом при оценке любого финансового инструмента является правильное определение порождаемых им денежных потоков. Для долговых инструментов, к числу которых относятся облигации, такими потоками являются периодически выплачиваемые проценты (купонный доход) и сумма долга (номинал облигации), которая обычно возвращается в конце срока облигации, хотя возможны и другие варианты ее погашения. Если выплата процентов не предусмотрена, то доход реализуется в форме разницы в ценах продажи и выкупа облигации (в виде дисконта). Широко распространенный и наиболее удобный для анализа вид долговых ценных бумаг – срочные безотзывные купонные облигации, предполагающие равномерную выплату фиксированного купонного дохода. Общий денежный поток от владения этими инструментами складывается из двух компонентов – сумма купонного дохода и величина номинала, погашаемая по окончании срока долга. Соответственно, общая формула определения внутренней стоимости такой облигации (Рв) будет иметь вид:
|
|
|
, (1)
где PVC – приведенная стоимость купонных выплат,
PVN – приведенная стоимость суммы погашения долга
Или
, (2)
где С – ежегодный купонный доход,
N – номинал облигации;
r – ставка сравнения (желаемая инвестором норма доходности),
n – срок до погашения облигации,
i – номер года, за который выплачивается купонный доход.
Равномерные выплаты купонного дохода представляют собой аннуитет, приведенная стоимость которого суммируется с приведенной стоимостью разовой выплаты нарицательной стоимости облигации в конце срока. Принципиально важную роль в этом расчете имеет ставка сравнения r, которая представляет собой альтернативную стоимость денежных средств для инвестора (см. § 3.3). В случае неизменной величины купонного дохода и процентной ставки r, первое слагаемое формулы (2) может быть представлено в более удобном для использования виде (формула 4 из § 2.3):
, (3)
Такое представление позволяет избежать громоздкой процедуры многократного дисконтирования годового дохода и последующего суммирования полученных результатов. Еще одним важным преимуществом такой формы представления является возможность использования финансовых таблиц, в которых приводятся значения множителей дисконтирования (второй сомножитель в формуле 3). При выплате купонного дохода два раза в год (что является общепринятой практикой), формула (2) несколько изменится:
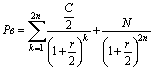, (4)
где k – номер полугодия, в котором производится выплата.
|
|
|
Применив формулу 13 из § 2.3, можно преобразовать выражение (3):
(5)
В этом случае ставка сравнения r становится номинальной процентной ставкой, поэтому при выплате дохода чаще, чем два раза в год можно легко преобразовывать базовую формулу, используя правила дисконтирования p-срочных аннуитетов с m = p (см. §. 2.3).
Аналогичные преобразования можно производить и с базовыми формулами (2) и (4). При этом годовую сумму купонного дохода (С) следует делить на число его выплат в течение года; точно так же надо поступать и со ставкой сравнения (r); срок до погашения облигации (n), наоборот, следует увеличить в такое же число раз. Большим преимуществом использования менее удобных формул (2) и (4) является возможность подстановки в них изменяющихся во времени значений купонного дохода С и ставки сравнения r. Условия облигационного займа могут предусматривать выплату переменного, а не постоянного купона. Величина ставки сравнения зависит от многих факторов, прежде всего – от уровня ставки рефинансирования Центрального банка. Поэтому в соответствующие формулы можно ввести не постоянные величины C и r, а переменные – Ck и rk.
Рассмотрим пример: номинал облигации 10 тыс. рублей, срок – 3 года, купонная ставка – 20%, выплата купона 1 раз в год (в конце года). Найти ее внутреннюю стоимость, если приемлемая для инвестора ставка сравнения составляет 25% годовых. Ожидаемый денежный поток от владения облигации можно представить следующим образом:
тыс. руб.
| Виды выплат | 1 год | 2 год | 3 год |
| Купонный доход | |||
| Возврат суммы долга | – | – | |
| Итого |
По формуле (2) получим:
Для инвестора имеет смысл приобретение облигации по цене не дороже 9, 024 тыс. рублей. Точно такой же результат будет получен с использованием формул (1) и (3):
Имея под рукой финансовые таблицы, инвестор мог бы выполнить этот же расчет следующим образом: для купонного дохода величину дисконтного множителя следует найти в таблице дисконтирования аннуитетов. При n = 3 и r = 25% он составит 1,952. Для номинала облигации дисконтный множитель следует искать в другой таблице – определения текущей величины единичных сумм. Он составит 0,512. Таким образом, внутренняя стоимость облигации будет равна:
Предположим, что купонный доход выплачивается в конце каждого полугодия в сумме 1 тыс. рублей (2 / 2). В этом случае следует применить формулу (4):
Внутренняя стоимость облигации теперь несколько ниже и составляет 8,987 тыс. руб. Этот же самый результат будет получен, если применить формулы (1) и (5):
|
|
|
При использовании финансовых таблиц необходимо искать дисконтные множители для срока 6 (3 х 2) и процентной ставки 12,5% (25 / 2). Для аннуитета такой множитель составит 4, 054, а для разового платежа – 0,493. Тогда
Заслуживает внимания факт, что выплата купонного дохода чаще, чем 1 раз в год, снижает внутреннюю стоимость облигации. Причем занижение происходит за счет более быстрой уценки номинала, который в любом случае выплачивается всего 1 раз в конце срока. Представляется, что такой результат не отражает реальной картины, так как инвестору выгоднее получать доход более частыми платежами. Читатель может убедиться сам, что использование для всех расчетов непрерывной процентной ставки δ позволило бы устранить данный логический казус. Так же самостоятельно следует определить внутреннюю стоимость облигации при условии изменяющейся суммы годового купона и переменной ставки сравнения (в этом случае могут быть использованы только формулы (2) и (4)).
В случае эмиссии облигаций с нулевым купоном денежный поток характеризуется лишь одной суммой – номиналом облигации, который будет выплачен владельцу по истечении ее срока. Следовательно, формула определения внутренней стоимости облигации упрощается, необходимо продисконтировать только одну сумму:
(6)
В рассмотренном выше примере при условии отсутствия купонных выплат, внутренняя стоимость облигации составит
(7)
То есть, данную облигацию не следует покупать по цене выше 5,12 тыс. рублей.
Правительства некоторых государств (например, Великобритании) эмитируют бессрочные облигации (консоли, военные займы), по которым периодически выплачивается фиксированная сумма дохода. В этом случае денежный поток представляет собой вечную ренту, приведенная стоимость которой (а следовательно, и внутренняя стоимость облигации) находится по известной формуле:
(8)
Например, по бессрочной облигации установлен ежегодный доход в сумме 600 рублей, ставка сравнения составляет 30%. Внутренняя стоимость такой облигации составит:
Иными словами, перспектива ежегодного получения 600 рублей в течение необозримого будущего для инвестора, альтернативная стоимость денежных средств для которого составляет 30% годовых, оценивается в 2 тыс. рублей. Если такую облигацию удастся купить дешевле, то NPV данной сделки будет положительной и она принесет выгоду покупателю. Периодичность выплат внутри года не оказывает влияния на стоимость такой облигации.
Как финансовый инструмент акция имеет немало существенных отличий от облигации: по обыкновенной акции не гарантируется обязательная выплата дохода (дивиденда), его величина может меняться во времени, возможны значительные колебания рыночной стоимости акции. В целом акции являются более рискованным инструментом, в сравнении с облигациями, однако они приносят владельцам более высокий доход. Внутренняя цена акции представляет дисконтированную сумму всех ожидаемых дивидендных выплат по ней плюс приведенная величина изменения ее рыночной стоимости. В отличие от облигации эмитент не обязан выкупать у инвестора акцию, однако инвестор может продать ее на вторичном фондовом рынке.
, (9)
где Div – годовая сумма дивидендов по акции (предполагается неизменной в течение всего срока владения ею);
Pпрод – цена, по которой планируется продать акцию в конце ее срока.
Одним из принципов ведения бизнеса является предположение о непрерывности работы предприятия в обозримом будущем: если не доказано обратное, считается, что предприятие будет продолжать свою деятельность бесконечно долго. Так как обыкновенные акции не имеют срока погашения, то распространяется этот принцип и на них, то есть их следует рассматривать как вечные ценные бумаги. Но по мере стремления периода владения (n) к бесконечности, величина второго слагаемого формулы (9) будет стремиться к нулю, т.е. дисконтированная стоимость продажной цены будет превращаться в бесконечно малую величину. Следовательно, при достаточно больших n ею можно пренебречь и определять внутреннюю стоимость акции только по первому слагаемому формулы (9) – дисконтированной сумме ожидаемых дивидендов. Но так как сумма этих дивидендов остается неизменной, то возникает вечная рента, приведенная величина которой (а следовательно, и внутренняя стоимость акции) должна находиться по формуле:
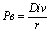(10)
Эта формула является универсальной, так как даже если инвестор собирается в скором времени перепродать акцию на вторичном рынке, он должен понимать, что цена ее продажи будет обусловлена суммой дивидендов, которую рассчитывает получить по ней ее новый покупатель. В конечном итоге второе слагаемое формулы (9) определяется суммой ожидаемых по акции дивидендов, поэтому при предположении неизменной суммы дивидендных выплат по акции для ее оценки используется формула (10). Выплата более или менее стабильных дивидендов предусмотрена по привилегированным акциям, которые занимают промежуточное положение между обыкновенными акциями и облигациями. Формула (10) чаще всего используется для оценки именно привилегированных акций. Например, по привилегированной акции ежегодно выплачивается дивиденд в сумме 300 рублей. Требуемая норма доходности (альтернативная цена капитала для инвестора) составляет 35%. Тогда внутренняя стоимость этой бумаги будет равна:
То есть максимально возможная цена покупки этой акции для данного инвестора составит 857 руб. 14 коп. Дивиденды могут выплачиваться чаще, чем 1 раз в год, например, поквартально. Однако (как уже говорилось в предыдущей главе), на результат вычислений по формуле (10) это не влияет. Достаточно разделить на 4 и числитель и знаменатель формулы, и будет получен тот же самый результат:
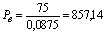
Если несколько усложнить модель, предположив равномерное увеличение суммы выплачиваемых дивидендов в будущем, то формула (10) примет вид:
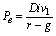, (11)
где Div1 – дивиденд, который должен быть выплачен в 1-м году планируемого периода,
g – планируемый темп прироста дивидендов.
Данная формула называется по имени ее автора моделью Гордона и широко используется для оценки обыкновенных акций крупных и многоотраслевых компаний. Если известен уровень дивидендов, выплаченных в базисном по отношению к планируемому периоде (Div0), то ее можно представить в следующем виде:
(12)
Предположив, что в рассмотренном выше примере сумма 300 рублей отражает величину дивиденда, выплаченного по обыкновенной акции в базисном периоде, а в дальнейшем планируется ежегодный 3-процентный прирост дивидендов, получим:
Ожидание даже небольшого роста дивидендов заметно увеличивает внутреннюю стоимость акции.
Хорошее знание математики позволяет от модели постоянного роста перейти к еще более сложным моделям, предусматривающим изменяющиеся во времени темпы прироста дивидендов. Соответственно будут усложняться и формулы расчетов. Однако данное усложнение ни коим образом не повышает надежность моделей, так как все зависит от точности предсказания темпов прироста. Повышению его точности может способствовать предварительный технический анализ, изучение трендов и построение корреляционно-регрессионных моделей. Все это относится скорее к инструментарию математической статистики, чем в финансовой теории. Более того, одной из широко распространенных финансовых концепций является признание невозможности предсказывать изменение цены акций на основании изучения только исторических данных. Более подробно данный вопрос будет рассмотрен в последующих главах.
Рассмотренные методы оценки ценных бумаг базируются на едином теоретическом фундаменте – дисконтировании денежных потоков. Данный подход не является единственно возможным. В практике оценки обыкновенных акций так же широко используется отношение “цена-доходы” (P/E), модель оценки финансовых активов Шарпа (CAPM). В последнее время очень быстро растет популярность производных ценных бумаг (опционы, фьючерсы), специфика которых обусловливает применение методов оценки, существенно отличающихся от рассмотренных выше; немало особенностей в способах оценки конвертируемых ценных бумаг и облигаций с правом их выкупа. Большинство из этих особенностей рассматриваются в рамках курсов “Финансовый анализ” и “Управление финансовыми ресурсами”.
Дополнительная литература к главе 3
- Белых Л.П. Основы финансового рынка. – М.: Финансы, ЮНИТИ, 1999, стр. 82 – 100.
- Брейли Р., Майерс С. Принципы корпоративных финансов. – М.: ЗАО “Олимп-Бизнес”, 1997, стр. 47 – 74, 101 – 138.
- Бригхем Ю., Гапенски Л. Финансовый менеджмент (т. 1). – СПб.: Экономическая школа, 1998, стр. 102 – 131, 362 – 366.
- Ван Хорн Дж. К. Основы управления финансами. – М.: Финансы и статистика, 1996, стр. 86 – 132, 381 – 385.
- Вэйтилингем Р. Руководство по использованию финансовой информации Financial Times. – Финансы и статистика, 1999, стр. 26 – 31.
- Ковалев В.В. Управление финансами. – М.: ФБК-ПРЕСС, 1998, стр. 27 – 34, 121 – 123.
- Ковалев В.В. Финансовый анализ. – М.: Финансы и статистика, 1997, стр. 201 – 216, 303 – 306.
- Макконелл Кэмпбелл Р., Брю Стэнли Л. Экономикс (т. 2). – М.: Республика, 1992, стр. 45 – 64.
- Райан Б. Стратегический учет для руководителя. – М.: Аудит, ЮНИТИ, 1998, стр. 52 – 128.
Финансовые рынки
|
|
|
