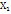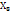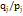 |
Работа с матрицей результатов
|
|
|
|
Для проверки тестовых свойств заданий тестовой формы и превращения части из них в тестовые задания, с данными (таблица 1) делается ряд расчетов. Результаты представлены в таблице 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | 0,9 | 0,1 | 9 | 2,19722 |
| 2 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 8 | 0,8 | 0,2 | 4 | 1,38629 |
| 3 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 7 | 0,7 | 0,3 | 2,333 | 0,8473 |
| 4 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 6 | 0,6 | 0,4 | 1,5 | 0,40547 |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 6 | 0,6 | 0,4 | 1,5 | 0,40547 |
| 6 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 5 | 0,5 | 0,5 | 1 | 0 |
| 7 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 5 | 0,5 | 0,5 | 1 | 0 |
| 8 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 5 | 0,5 | 0,5 | 1 | 0 |
| 9 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 4 | 0,4 | 0,6 | 0,667 | -0,4055 |
| 10 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 4 | 0,4 | 0,6 | 0,667 | -0,4055 |
| 11 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0,3 | 0,7 | 0,429 | -0,8473 |
| 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0,2 | 0,8 | 0,25 | -1,3863 |
| 13 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,1 | 0,9 | 0,111 | -2,1972 |
|
| 12 | 11 | 9 | 7 | 6 | 6 | 5 | 4 | 3 | 2 | 65 |
|
|
|
|
|
| 1 | 2 | 4 | 6 | 7 | 7 | 8 | 9 | 10 | 11 |
|
|
|
|
|
|
| 0,923 | 0,846 | 0,692 | 0,538 | 0,462 | 0,462 | 0,385 | 0,308 | 0,231 | 0,154 | 5 |
|
|
|
|
|
| 0,077 | 0,154 | 0,308 | 0,462 | 0,538 | 0,538 | 0,615 | 0,692 | 0,769 | 0,846 |
|
|
|
|
|
|
| 0,071 | 0,13 | 0,213 | 0,249 | 0,249 | 0,249 | 0,237 | 0,213 | 0,178 | 0,13 |
|
|
|
|
|
|
| 0,083 | 0,182 | 0,444 | 0,857 | 1,167 | 1,167 | 1,6 | 2,25 | 3,333 | 5,5 |
|
|
|
|
|
|
| -2,48 | -1,7 | -0,81 | -0,15 | 0,154 | 0,154 | 0,47 | 0,811 | 1,204 | 1,705 |
|
|
|
|
|
Таблица 2. Матрица результатов с расчётами
В этой матрице проведено два упорядочения.
Одно касается испытуемых. В первой строке представлены баллы самого успешного испытуемого, во второй менее, и т.д., по нисходящей сумме баллов, если ее посчитать для каждого испытуемого.
|
|
|
Другое упорядочение проведено для заданий. На первом месте стоит самое легкое задание, по которому имеется наибольшее число правильных ответов, на втором - меньшее, и т. д., до последнего, у которого имеется всего один правильный ответ.
В таблице 2 приводятся и основные статистические данные, которые принимаются во внимание на первом этапе эмпирической проверки качества заданий.
Вначале определяется мера трудности заданий. Известную трудность заданий, как первое требование к тестовым заданиям, можно образно сравнить с разновысокими барьерами на беговой дорожке стадиона, где каждый последующий барьер чуть выше предыдущего. Успешно преодолеть все барьеры сможет только тот, кто лучше подготовлен.
Трудность задания может определяться двояко:
1)умозрительно – то есть на основе предполагаемого числа и характера умственных операций, которые необходимы для успешного выполнения задания;
2)эмпирически - путем опробования задания, с подсчетом доли неправильных ответов по каждому из них.
Эмпирически трудность заданий можно определить, сложив элементы матрицы по столбцам, что укажет на число правильных ответов, полученных по каждому заданию (
). Чем больше правильных ответов на задание, тем оно легче для данной группы испытуемых.
Больше правильных ответов оказалось в первом задании (
= 12), это значит, что оно самое легкое в матрице.
В классической теории тестов многие годы рассматривались только эмпирические показатели трудности. В новых вариантах психологических и педагогических теорий тестов больше внимание стало уделяться,помимо эмпирических показателей, характеру умственной деятельности учащихся в процессе выполнения тестовых заданий различных форм.
В силу простоты показатель 
, удобен, но до тех пор, пока не появляются другие группы испытуемых, с разным числом испытуемых (
). Поэтому для получения сопоставительных характеристик , делят на число испытуемых в каждой группе.[4]
|
|
|
В результате получается нормированный (числом испытуемых) статистический показатель - доля правильных ответов, 
. Значения 
приводятся в третьей строке нижней части таблицы 2.
Статистика долгое время использовалась в качестве показателя трудности в так называемой классической теории тестов. Позже была осознана содержащаяся в ней смысловая неточность: ведь увеличение значения указывает не на возрастание трудности, а, наоборот, на возрастание легкости, если можно применить такое слово.
Поэтому в последние годы с показателем трудности заданий стали ассоциировать противоположную статистику - долю неправильных ответов (
). Эта доля вычисляется из отношения числа неправильных ответов (
- вторая строка нижней части таблицы) к числу испытуемых (
):
Значения 
представлены в четвертой строке нижней части таблицы 2. Естественным образом принимается, что
Результаты сложения по строкам представлены в последнем столбце таблицы. Из последнего, одиннадцатого столбца таблицы видно, что больше правильных ответов у первого испытуемого, а меньше - у последнего. Это столбец представляет собой числовой вектор тестовых баллов испытуемых. Суммирование баллов всех испытуемых, представленных в таблице, дает число 65. Полезно посчитать средний арифметический тестовый балл в данной группе испытуемых
(4)
Это равенство отражает сумму всех элементов матрицы тестовых заданий, но только для случаев, когда для получения 
используются одинаковые весовые коэффициенты (
) значимости заданий в тесте, все равные, например, единице.
|
|
|
