 |
Подобие течений в компрессорах и их характеристики
|
|
|
|
2.19. Одним из условий обеспечения подобия режимов работы компрессора является выдерживание неизменного значения приведенной частоты вращения 
. В условиях задачи полная температура воздуха на входе в компрессор в полете равна 
а на стенде 
Тогда в полете 
10692,9 об/мин, а на стенде необходимо выдерживать частоту вращения 
2.20. Приведенная частота вращения на земле в САУ 
Из условия равенства приведенной частоты вращения на земле и в полете найдем температуру воздуха на входе в двигатель в полете 
при том же значении 
, если в полёте 
Так как , то 
251,89 К.
Согласно табл. 1 Приложения на Н = 11 км температура ТН = 216,77 К. Тогда, используя формулу 
, найдем:
0,9.
2.21. На старте в САУ приведенная частота вращения равна физической, так как 
. Если физическая частота вращения не изменяется, то и в полете для получения такого же значения температура 
также должна иметь значение 
. Для этого число М полета на высоте 
11 км (см. решение задачи 2.26) должно быть равно
1,282.
2.22. На подобных режимах приведенный расход воздуха через компрессор остается одним и тем же. Так как 
, то на стенде в САУ при 
(т.е. при 
101300 Па и 
288 К) приведенный расход воздуха равен физическому, т.е. 
100 кг/с.
Тогда, так как ,
то в полете 
,
где при 
54050 Па и 
255,7 К (на высоте 5 км)
; 
.
Следовательно, в полете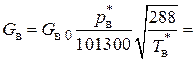 
78,0 кг/с.
2.23. Работа, затрачиваемая на вращение компрессора, равна
, где 
.
Тогда из условия равенства работ и равенства КПД компрессора на стенде (в стандартных атмосферных условиях) и в полете следует, что
,
откуда (при 
2,1255 и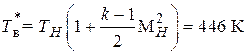 
) в полете
1,7268; т.е. 
6,76.
2.24. Для условий полета на высоте Н = 11 км (где 22700 Па и 216,8 К) определим полные параметры воздуха на входе в двигатель (в компрессор) при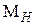 
= 2,05:
|
|
|
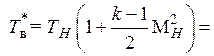399 К; 
172,8 кПа.
Тогда приведенная частота вращения компрессора в полете составит (при 
) 
При этом значении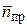 
с характеристики компрессора (в точке пересечения рабочей линии и напорной ветви 
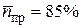, см. рис. 2.6) снимаются значения: 
а такому значению 
при 
85% согласно рис. 2.6 соответствует 
На этой же напорной ветви на границе устойчивой работы (ГУР) компрессора 
и 
.
Тогда запас устойчивости компрессора в условиях полета равен
,
а расход воздуха у этого компрессора в условиях полета равен
ГАЗОВЫЕ ТУРБИНЫ ГТД
3.1. Работа 
на окружности колеса ступени турбины равна
3.2. Согласно уравнению сохранения энергии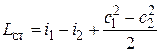 
. По условию задачи 
. Следовательно, в данном случае
.
Но 
. Тогда 
3.3. Из треугольника скоростей на входе в рабочее колесо (см. рис.3.2) следует: 
1,1806 и тогда 
49,7о.
Кроме того, так как 
, то и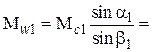 
0,426.
3.4. Полная температура газа на выходе из ступени турбины определится из уравнения сохранения энергии, согласно которому
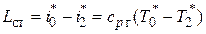. Отсюда (при 
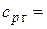1246 Дж/(кг×К))
Так как 
, то в условиях задачи 
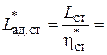431,8 кДж/кг. Тогда из формулы для адиабатной работы ступени 
найдем: 
0,210, что (при k г = 1,3) соответствует 
2,78.
Следовательно 
3.5. Работа на валу турбины равна (при 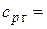1246 Дж/(кг×К))
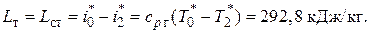
Значению 
= 0,35 при 
соответствует П(l2) = 0,9326 (см. Приложение, табл. 4). Тогда полное давление за турбиной
и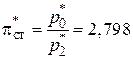 
.
По найденному значению 
определим КПД турбины в параметрах заторможенного потока. Располагаемый теплоперепад (адиабатная работа расширения газа) в параметрах заторможенного потока равен
, где 
1,268.
Тогда 
Располагаемый теплоперепад в статических параметрах равен
, где 
1,2886,
так как 
. Тогда мощностной КПД свободной турбины равен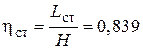 
.
3.6. Из формулы для коэффициента нагрузки ступени турбины
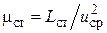найдутся работы на валах ТВД и ТНД:
и 
.
3.7. Мощность турбины равна 
. Соответственно работа турбины (при данной мощности) равна 
.
Тогда потребное число ступеней в турбине определится из формулы для среднего коэффициента нагрузки ступеней турбины: 
, где z – число ступеней. Если окружная скорость на среднем радиусе у всех сту-
|
|
|
пеней одинакова, то тогда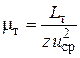 
. Тогда потребное число ступеней равно
, т.е. 
3.8. Пусть общее число ступеней в турбине равно 
. Обозначим коэффициент нагрузки последней ступени 
, а у остальных ступеней 
. Работа последней (z -ой) ступени турбины равна (см. решение задачи 3.6)
.
Тогда суммарная работа остальных ступеней турбины будет равна
.
Соответственно их число будет равно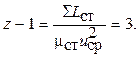 
Следовательно, общее количество ступеней турбины 
.
3.9. Если скорость газа направлена под углом 
к поперечному сечению «1 – 1» газового тракта ступени турбины, то расход газа через это сечение равен 
или 
, где (при k г = 1,30 и R г = 287,6 Дж/(кг×К)) m г = 0,0393. Тогда (при 
2,178 МПа и 
1550 К) 
.
Значение 
0,9992 находится здесь по величине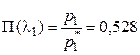 
Тогда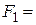 
0,0807 м2.
Но при 
площадь сечения «1-1» равна 
. Отсюда 
.
3.10. Площадь сечения проточной части на выходе из ступени турбины определится по той же формуле, которая использовалась при решении задачи 3.9: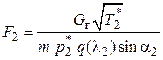 
, причем в данном случае 
.
Здесь 
, 
0,5941, а температура 
находится из уравнения сохранения энергии для ступени
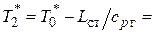1284 К;
где 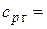1246 Дж/(кг×К) и 
331,3 кДж/кг.
Тогда 
0,1046 м2, а высота лопаток на выходе из ступени равна (при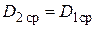 
) 
.
3.11. Температура газа на передней кромке рабочей лопатки ступени турбины 
равна 
. Но 
, следовательно,
.
Входящее сюда значение 
определятся по формуле (см. решение задачи 3.3) , где 
1,3423,
т.е. 
, что дает 
311,4 м/с.
3.12. На подобных режимах работы турбины
; 
.
Следовательно, при возрастании n на 20% значение 
увеличится также на 20%, а так как на подобных режимах 
, то при одновременном возрастании 
на 40% расход газа увеличится в 1,4/1,2 = 1,167 раз.
Таким образом, расход газа увеличится на 16,7%.
|
|
|
