 |
Обоснование применения метода Гаусса
|
|
|
|
Задание
Построить математическую модель расчета опорных реакций жесткого стержня с тремя опорными узлами и определение внутренних усилий, поперечной силы Q и изгибающего момента М, возникающих во внутренних сечениях стержня под действием нагрузки. Разработать алгоритм и составить программу вычисления опорных реакций и распределения вдоль оси стержня внутренних усилий.
Вариант - 82-4г. Схема - 2.
Численный метод решения СЛАУ - метод Гаусса.
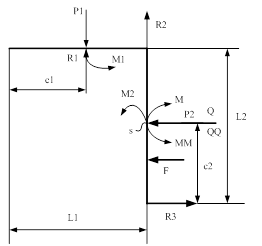
Схема нагруженного стержня
| |
q4 - интенсивность распределенной нагрузки, H/м
C1, C2 - отрезок балки, м
L1, L2 - пролет балки, м
М1, M2 - круговой момент, H 
м
Исходные данные
P1=15kH P2=30kH L1=6м L2=12м
M1=10kHм M2=35kHм С1=3м C2=2м
L1=6м L2=12м q4=10kH
|
Построение системы линейных алгебраических
уравнений для определения опорных реакций.
Преобразуем исходную систему:
отбросим опорные стержни и заменим их опорными
реакциями (R1; R2; R3)
интенсивность распределённой нагрузки заменим эквивалентной
силой (F4 = q4 c2)
зададим систему координат.
|
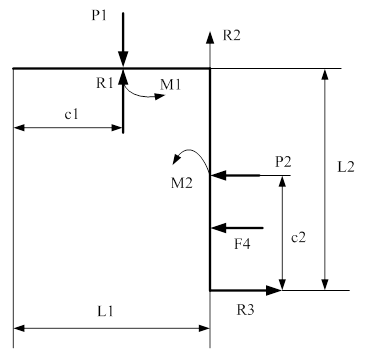
Для вывода формул вычисления опорных реакций запишем уравнение равновесия стержня: сумма моментов относительно опорной точки стержня равна нулю.
:
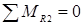
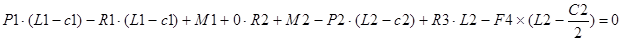
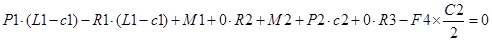
Представил уравнения равновесия балки в форме системы линейных алгебраических уравнений (СЛАУ).
Матричная форма записи СЛАУ вычисление опорных реакций балки
A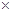 
R=B
А - матрица коэффициентов при неизвестных
R - матрица неизвестных
В - матрица свободных членов
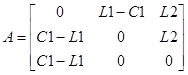
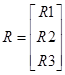
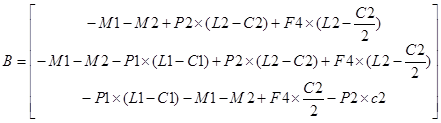
Вывод формул проверки, достоверности вычисления опорных реакций
|
|
|
Для проверки правильности вычисления опорных реакций использовал уравнения равновесия балки, сумма проекций всех сил действующих на балку равна нулю.
Y=R1-P1+R2=0
X=R3-P2-F4=0
Вывод рабочих формул определение внутренних усилий стержня
На рассматриваемом стержне выделим четыре участка длиной S (длина отрезка от начала до точки сечения стержня), для которых составим формулы для вычисления внутренних усилий: поперечной силы Q и изгибающего момента М.
s - отрезок от начала до точки сечения балки
I cечение 
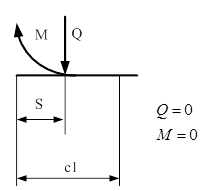
II cечение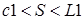 
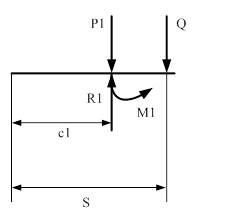
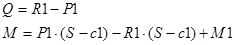
III cечение 
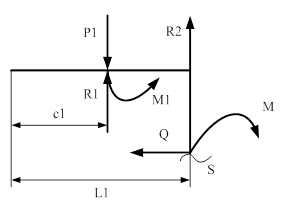
IV cечение 
В точках границ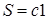 
, 
, 
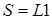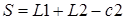организуем вычисления поперечной силы Q слева (и QQ справа), изгибающего момента М слева (и MМ справа) от рассматриваемых точек.
1 точка границ: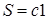
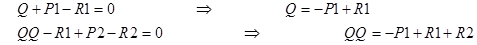
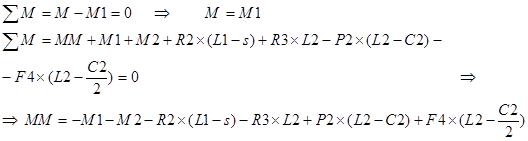
2 точка границ: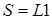
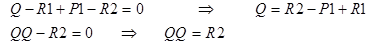
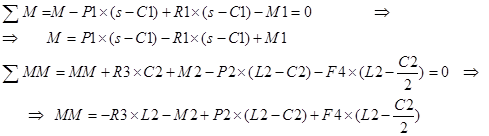
3 точка границ: 
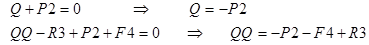
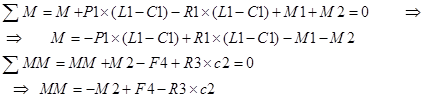
Численный метод решения СЛАУ - метод Гаусса
Численный метод Гаусса относится к точным методам решения системы линейных алгебраических уравнений. Он основан на приведении матрицы коэффициентов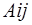 
к треугольному виду. Процесс поиска решения системы линейных алгебраических уравнений выполняется в два хода: прямой ход и обратный ход.
Прямой ход исключения переменных выполняется путём преобразования коэффициентов СЛАУ, коэффициенты при неизвестных обращаются в нуль, начиная со второго по формулам:
; 
; 
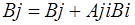, где
; 
; 
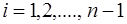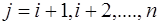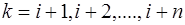
Процесс преобразования уравнений заканчивается последним уравнением. Результатом прямого хода является получение матрицы коэффициентов к треугольному виду.
Обратный ход (последовательное нахождение неизвестных
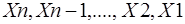) выполняется по формулам:
; 
; 
; 
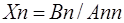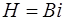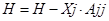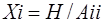, где
; 
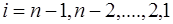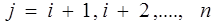
В результате формируется матрица неизвестных: 
Метод Гаусса для решения СЛАУ применим при условии, что все диагональные элементы матрицы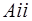 
отличны от нуля, т.е. 
, где 
.
|
|
|
Обоснование применения метода Гаусса
Исходная СЛАУ имеет на главной диагонали элементы равные нулю:
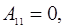
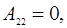
следовательно, метод Гаусса применять нельзя.
Для того чтобы использовать численный метод Гаусса для решения данной СЛАУ необходимо её преобразовать. Для этого необходимо применить к исходной СЛАУ схему выбора главных элементов. В исходной СЛАУ переставим уравнения местами: первое уравнение поставим на второе место, второе уравнение поставим на третье место, третье уравнение поставим на первое место.
В результате на главной диагонали матрицы А отсутствуют члены равные нулю.
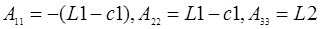
Для повышения точности получаемого решения СЛАУ матрица А должна быть диагонально преобладающей:
, 
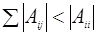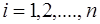
Преобразованная СЛАУ имеет вид:
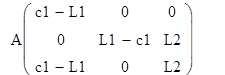
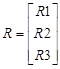
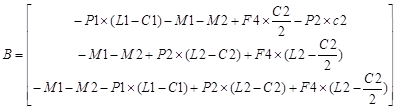
Условия применения метода Гаусса выполняются, следовательно, метод Гаусса можно использовать для решения преобразованной СЛАУ.
Блок - схема алгоритма
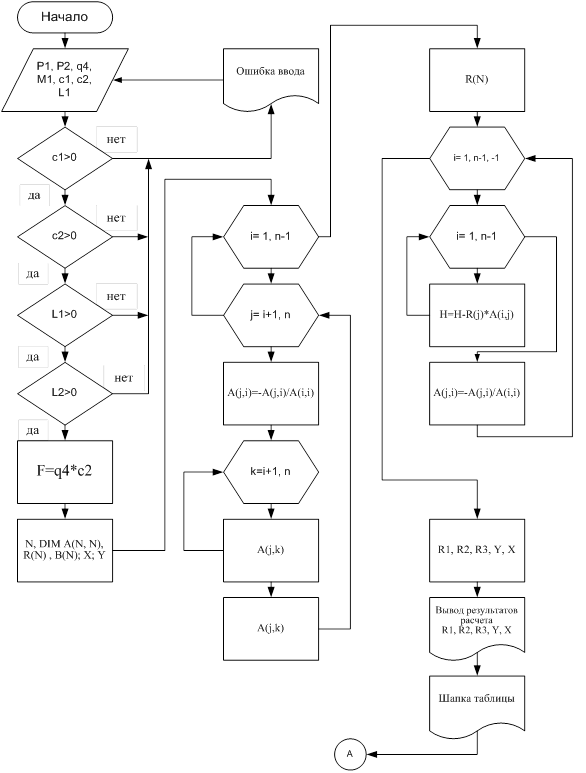
Программа
CLS
SCREEN 12
WINDOW (20, 20) - (-20, - 20)
N = 3
PRINT "Программу составил студент гр.320851 Клычников А.В."
50 PRINT " Расчет жесткого стержня "
PRINT " Исходные данные"
INPUT "Интенсивность распределения нагрузки q4 (кH/м) ="; q4
INPUT "Отрезок балки С1 (м) ="; C1
INPUT "Пролет балки L1 (м) ="; L1
INPUT "Отрезок балки C2 (м) ="; c2
INPUT "Пролет балки L2 (м) ="; L2
INPUT "Круговой момент M1 (кH*м) ="; M1
INPUT "Круговой момент M2 (кH*м) ="; M2
INPUT "Сосредоточенная сила P1 (кH) ="; P1
INPUT "Сосредоточенная сила P2 (кH) ="; P2
PRINT " "
IF C1 > 0 THEN GOTO 10 ELSE GOTO 40
10 IF c2 > 0 THEN GOTO 20 ELSE GOTO 40
20 IF L1 > C1 THEN GOTO 30 ELSE GOTO 40
30 IF L2 > c2 THEN GOTO 60 ELSE GOTO 40
40 PRINT "Ошибка ввода": GOTO 50
60 F = q4 * c2
DIM A (N, N), R (N), B (N)
A (1,1) = - (L1 - C1): A (1,2) = 0: A (1,3) = 0
A (2,1) = 0: A (2,2) = L1 - C1: A (2,3) = L2
A (3,1) = - (L1 - C1): A (3,2) = 0: A (3,3) = L2
B (1) = P1 * (L1 - C1) - M1 - F * (C1/2) - M2 - P2 * c2
B (2) = F * (L2 - c2/2) - M1 + P2 * (L2 - c2) - M2
B (3) = - P1 * (L1 - C1) - M1 + F * (L2 - c2/2) - M2 + P2 * (L2 - c2)
FOR I = 1 TO N - 1
FOR J = I + 1 TO N
A (J, I) = - A (J, I) / A (I, I)
FOR K = I + 1 TO N
A (J, K) = A (J, K) + A (J, I) * A (I, K): NEXT K
B (J) = B (J) + A (J, I) * B (I): NEXT J
NEXT I
R (N) = B (N) / A (N, N)
FOR I = N - 1 TO 1 STEP - 1: H = B (I)
FOR J = I + 1 TO N: H = H - R (J) * A (I, J): NEXT J
R (I) = H / A (I, I)
NEXT I
R1 = R (1): R2 = R (2): R3 = R (3)
X = R1 - P1 + R2
Y = R3 - P2 - F
PRINT " Результаты "
PRINT "Опорная реакция в точке 1 R1="; R (1); "kН"
|
|
|
PRINT "Опорная реакция в точке 2 R2="; R (2); "kН"
PRINT "Опорная реакция в точке 3 R3="; R (3); "kН"
PRINT "Y="; Y; " X="; X
PRINT " Таблица ординат эпюр Q и M "
PRINT " S Q M QQ MM"
FOR s = 0 TO L1 + L2
IF s >= 0 AND s < C1 THEN
Q = 0
M = 0
GOTO 70
END IF
IF s > C1 AND s < L1 THEN
Q = R1 - P1
M = P1 * (s - C1) - R1 * (s - C1) + M1
GOTO 70
END IF
IF s > L1 AND s < L1 + L2 - c2 THEN
Q = 0
M = P1 * (L1 - C1) - R1 * (L1 - C1) + M1
GOTO 70
END IF
IF s > L1 + L2 - c2 AND s <= L1 + L2 THEN
Q = - P2 - q4 * (s - L1 - L2 + c2)
M = P1 * (L1 - C1) - R1 * (L1 - C1) + M1 + M2 + P2 * (s - L1 - L2 + c2) + q4 * (s - L1 - L2 + c2) * (s - L1 - L2 + c2) / 2
GOTO 70
END IF
IF s = C1 THEN
Q = R1 - P1
M = M1
QQ = R2 - P1 + R1
MM = - M1 - R2 * (L1 - s) + P2 * (L2 - c2) - M2 - R3 * L2 + F * (L2 - c2/2)
GOTO 80
END IF
IF s = L1 THEN
Q = R1 - P1 + R2
M = P1 * (s - C1) - R1 * (s - C1) + M1
QQ = R2
MM = P2 * (L2 - c2) - M2 - R3 * L2 + F * (L2 - c2/2)
GOTO 80
END IF
IF s = L1 + L2 - c2 THEN
Q = - P2
M = M2 + P1 * (L1 - C1) - R1 * (L1 - C1) + M1 + F * (L1 - C1) / 2 - 30
QQ = R3 - P2 - F
MM = - M2 - R3 * c2 + F
GOTO 80
END IF
70 PRINT USING "##. ## ####. #### ####. ####"; s; Q; M: GOTO 90
80 PRINT USING "##. ## ####. #### ####. #### ####. #### ####. ####"; s; Q; M; QQ; MM
90 NEXT s
A$ = INPUT$ (1)
LINE (10,8) - (18,8), 8
LINE (10,3) - (10, 20), 8
FOR Z = 10 TO 18 STEP.5
LINE (Z, 7.9) - (Z, 8.1), 8
FOR W = 3 TO 20 STEP.5
LINE (9.9, W) - (10.1, W), 8
NEXT W
NEXT Z
LINE (10, - 3) - (18, - 3), 8
LINE (10, 0) - (10, - 18), 8
FOR Z = 10 TO 18 STEP.5
LINE (Z, - 2.9) - (Z, - 3.1), 8
FOR W = - 18 TO 0 STEP.5
LINE (9.9, W) - (10.1, W), 8
NEXT W
NEXT ZFOR T = 0 TO L1 + L2 STEP.001
IF T >= 0 AND T < C1 THEN
Q = 0
M = 0
V1 = Q
U1 = M
GOTO 100
END IF
IF T > C1 AND T < L1 THEN
Q = R1 - P1
M = P1 * (T - C1) - R1 * (T - C1) + M1
V2 = Q
U2 = M
GOTO 100
END IF
IF T > L1 AND T < L1 + L2 - c2 THEN
Q = 0
M = P1 * (L1 - C1) - R1 * (L1 - C1) + M1
V3 = Q
U3 = M
GOTO 100
END IF
IF T > L1 + L2 - c2 AND T <= L1 + L2 THEN
Q = - P2 - q4 * (T - L1 - L2 + c2)
M = P1 * (L1 - C1) - R1 * (L1 - C1) + M1 + M2 + P2 * (T - L1 - L2 + c2) + q4* * (T - L1 - L2 + c2) * (T - L1 - L2 + c2) / 2
GOTO 100
END IF
100 PSET (T / 3 + 10, Q / 3 + 8), 4
PSET (T / 3 + 10, M / 3 - 3), 5
NEXT T
T = C1: GOTO 110
110 Q = R1 - P1
M = M1
PSET (T / 3 + 10, Q / 3 + 8), 4
PSET (T / 3 + 10, M / 3 - 3), 5
LINE (T / 3 + 10, V1/3 + 8) - (T / 3 + 10, Q / 3 + 8), 4
LINE (T / 3 + 10, U1/3 - 3) - (T / 3 + 10, M / 3 - 3), 5
T = L1: GOTO 120
120 Q = R1 - P1 + R2
M = P1 * (T - C1) - R1 * (T - C1) + M1
PSET (T / 3 + 10, Q / 3 + 8), 4
PSET (T / 3 + 10, M / 3 - 3), 5
LINE (T / 3 + 10, V2/3 + 8) - (T / 3 + 10, Q / 3 + 8), 4
LINE (T / 3 + 10, U2/3 - 3) - (T / 3 + 10, M / 3 - 3), 5
T = L1 + L2 - c2: GOTO 130
130 Q = - P2
M = M2 + P1 * (L1 - C1) - R1 * (L1 - C1) + M1 + F * (L1 - C1) / 2
PSET (T / 3 + 10, Q / 3 + 8), 4
PSET (T / 3 + 10, M / 3 - 3), 5
LINE (T / 3 + 10, V3/3 + 8) - (T / 3 + 10, Q / 3 + 8), 4
LINE (T / 3 + 10, U3/3 - 3) - (T / 3 + 10, M / 3 - 3), 5
END
|
|
|
