Главная | Обратная связь | Поможем написать вашу работу!

Исследование движения жидкости и механических примесей в ней методом конечных элементов

Движение жидкости будет турбулентным. Турбулентные движения характеризуются тем, что поле истинных скоростей частиц жидкости, которая рассматривается как сплошная среда-континуум, имеет нерегулярный пульсационный характер, является неустановившимся и напоминает хаотическое поле скоростей отдельных молекул, из которых состоят тела. Траектории частиц жидкости при турбулентном движении в высшей степени извилисты. Точные измерения указывают на то, что изменения всех параметров течения при турбулентном движении во времени имеют вид, изображенный на рисунке 2.1, где для примера дано характерное для турбулентных течений изменение плотности в данной точке пространства с течением времени t.

Рис 2.2 Плотность турбулентного течения

На основное изменение плотности (на рисунке- плавная пунктирная линия) накладываются нерегулярные пульсации большой частоты.

Во многих вопросах турбулентные течения жидкости целесообразно изучать только в среднем. При исследовании турбулентных течений обычно вводят средние значения компонент скорости , , , давления 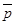, плотности , температуры и других характеристик движения (черточки над буквами здесь и далее обозначают осреднение). Для определения средних характеристик движения можно ставить и решать математические задачи [2].

Таким образом, в случае турбулентных течений сложное движение жидкости осредняется и при этом возникают проблемы составления полной системы уравнений для определения средних характеристик движения и проблемы изыскания способов экспериментального измерения осредненных характеристик движения.

Практика построения моделей для изучения турбулентных движений показывает, что способы введения средних характеристик движения, вообще говоря, несущественны для составления полной системы уравнений теорий турбулентности, но они являются главной основой для разработки методов экспериментальных измерений различных средних величин, проведение которых необходимо для сравнения результатов предложенной теории турбулентности с опытными данными.

Укажем некоторые возможные способы осреднения истинных характеристик движения. Пусть А(х,у,z,t) - некоторая истинная характеристика турбулентного движения. В любой фиксированной точке пространства можно провести осреднение А по времени t. Тогда среднее значение А будет равно

где промежуток времени Т достаточно велик по отношению ко времени отдельных пульсации и мал по отношению ко времени заметного изменения средних характеристик (осредненное движение может быть нестационарным).

С другой стороны, в определенный момент времени t осреднение А можно провести по объему; тогда

причем объем V должен удовлетворять условиям, аналогичным условиям, наложенным на промежуток времени Т. Можно провести осреднение по времени и по объему V одновременно.

Указанные выше осреднения по времени и по объему возможно проводить с весом, когда среднее значение А определяется, например, следующим образом:

где g(t) - некоторая заданная функция. В различных задачах при выборе V и Т можно руководствоваться различными соображениями, но в имеющихся приложениях результат осреднения рассматривается как не зависящий от V и T.

В ряде случаев используются вероятностные способы осреднения, и среднее значение A часто определяется как математическое ожидание A.

После введения среднего значения A истинное значение A представляется в виде

A= +A',

где A'-пульсация A; среднее значение пульсации равно нулю, ' = 0.

Потребуем, чтобы операции осреднения во всех случаях обладали следующими свойствами:

1 Среднее значение суммы равняется сумме средних значений:

= + .

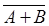2 Среднее значение производной от истинной характеристики турбулентного движения равняется производной от среднего значения:

Среднее значение произведения двух сомножителей, из которых только один испытывает турбулентные пульсации, равно произведению средних. В частности, =0. Среднее значение произведения двух пульсирующих величин не равняется произведению средних:

а равняется сумме произведения средних величин и среднего значения произведений пульсации этих величин:

Заметим, что при определении средних значений с помощью интегрирования по времени или по пространству перечисленные здесь свойства осреднения выполняются лишь приближенно. Пусть проведено осреднение скорости u= +u'. Среднее значение u² не равняется квадрату среднего значения u:

= ²+ .

Можно назвать средним значением u² макроскопическую величину , введенную, например, по формуле

= ².

Для истинных значений u² в этом случае можно написать

причем , но .

Если в механике жидкости для величин ввести средние одинаковым способом, то характеристики движения таким образом осредненного континуума не будут удовлетворять основным законам сохранения и уравнениям состояния, удовлетворяющимся для истинных движений.

В различных теориях турбулентности для определенного набора основных величин осреднения вводятся некоторым одинаковым способом, а способы осреднения других величин вводятся по соглашению так, чтобы удовлетворялись основные законы физики, как и при обычном определении этих величин для истинных движений.

Рассмотрим турбулентные движения несжимаемой вязкой жидкости. Полная система уравнении движения в этом случае, как известно, состоит из уравнения неразрывности и уравнений импульса, которые в декартовой системе координат имеют вид

,(2.7)

, (2.8)

где - компоненты тензора вязких напряжений. Для вязкой жидкости зависят от , для изотропной линейной вязкой несжимаемой жидкости по закону Навье - Стокса

, . (2.9)

Для дальнейшего мы не будем фиксировать закон зависимости от 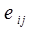, заметим только, что в общем случае 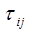могут зависеть от производных . Используя уравнение неразрывности (2.7) и условие , легко показать, что левую часть уравнений Навье - Стокса можно написать в виде

. (2.10)

При многих теоретических исследованиях турбулентных движений исходят из предпосылки о справедливости уравнений (2.7),(2.8) для истинного неустановившегося пульсирующего движения. Однако ввиду крайней запутанности, извилистости и сложности траекторий частиц жидкости при турбулентном движении получение решений этих уравнений для турбулентных движений представляет собой громоздкую и сложную задачу. Ставится задача о разыскании функциональных соотношений между средними величинами. Уравнения движения для средних, величин получаются путем осреднения уравнений движения (2.7),(2.8) для величин, описывающих мгновенное состояние движения.

Осреднив уравнение неразрывности (2.7), на основании свойств операции осреднения легко получим уравнение неразрывности для осредненных величин

;(2.11)

оно имеет тот же вид, что и для истинных скоростей (2.7).

Осредним уравнения импульса, левую часть которых предварительно запишем в виде (2.10). Так как

, (2.12)

(плотность считается постоянной, одинаковой во всех точках), то, получим следующие уравнения:

(i=1,2,3), (2.13)

которые называются уравнениями Рейнольдса.

Если связь и (и, возможно, производных ) линейная и = const, то выражаются через так же, как через . Поэтому, уравнения Рейнольдса (2.13) отличаются от уравнений импульса (2.8) для истинных движений только за счет членов вида

Шесть различных величин

вошедших в уравнения Рейнольдса, называются турбулентными напряжениями. Вид зависимости турбулентных напряжений от средних характеристик течения в различных классах задач может быть различным.

Таким образом, ввиду нелинейности уравнений истинных движений, после их осреднения получается большее, чем число уравнений, число неизвестных. Следовательно, для математического изучения осредненных турбулентных движений одних уравнений гидромеханики, достаточных для изучения истинных движений, недостаточно. Поэтому полное теоретическое исследование осредненных турбулентных движений возможно только на основании некоторых дополнительных законов или гипотез, справедливость которых может быть в конечном счете установлена только на опыте.

Содержание многих работ по исследованию турбулентных движений [2,10,11,12,13] сводится к изучению справедливости различных простых и естественных гипотез о зависимости турбулентных напряжений от средних скоростей и их градиентов, которые позволяют поставить и решить теоретически основные частные задачи о турбулентном движении. В настоящее время не существует общей математической постановки задачи о произвольных осредненных турбулентных движениях и вообще не выяснена возможность такой формулировки задачи.

Иногда по аналогии с законом Навье - Стокса (2.9) полагают, что

, (2.14)

где M₁= +M, М - коэффициент турбулентной вязкости, который в противоположность коэффициенту молекулярной вязкости , зависит от переменных кинематических характеристик осредненного движения жидкости. Согласно [14], выдвинем гипотезу

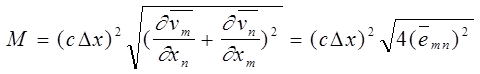,(2.15)

где с=[0,1:0,2], Dx- шаг сетки (при вычислении методом конечных элементов).

Найдем

, (2.16)

,(2.17)

т.к. по свойствам осредненной функции скорости и учитывая уравнение неразрывности (2.11)

, (2.18)

подставим (2.17) и (2.18) в (2.16), получим

(2.19)

подставим (2.19) в (2.13), получим замкнутую систему уравнений

(2.20)

(i,k,m,n=1,2,3) (2.21)

Осталось только добавить начальные и граничные условия

(i=1,2,3)

Решить эту систему в общем случае аналитически нельзя, она решается численными методами, например методом конечных элементов. Вычисления проводились в системе ANSYS, картину распределения поля скоростей и давления можно увидеть на рис 2.3 и рис 2.4.

Рис 2.3 Поле распределения скоростей в баке (v₀=2,358 м/с)

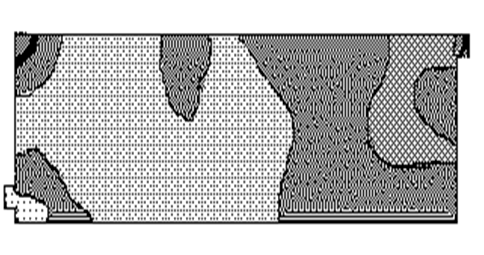
Рис 2.4 Поле распределения давления в баке

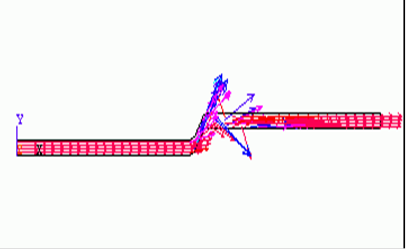
Рис 2.5 Поле распределения скоростей в трубопроводе (v₀=3,537 м/с)

Начальное значение скорости вычисляется исходя из расхода жидкости

(2.22)

где Q - расход жидкости (м³/с), d - диаметр трубопровода (м).

Теперь рассмотрим турбулентное движение жидкости с примесями. Предположим, что движение жидкости не зависит от присутствующих в ней примесей, т.к. дисперсный состав и концентрация примесей очень малы. Считаем частичку примеси шаром радиуса R, тогда, можно рассмотреть силы, действующие со стороны жидкости на эту частицу: F_A - выталкивающая сила (Архимедова), P - сила давления, F - сила сопротивления, mg - сила тяжести, U - скорость движения частицы. Считаем, что жидкость линейно-вязкая, т.е. представляет собой сплошную среду, в которой сопротивление сдвигу пропорционально скорости движения.

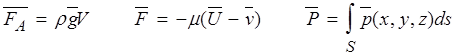
где V - объем частицы примеси, - вектор осредненной скорости жидкости, S - площадь поверхности частицы примеси, (x,y,z) - давление со стороны жидкости в точке (x,y,z) направленное по нормали к поверхности шара, m - коэффициент вязкости жидкости, r - плотность жидкости, - вектор скорости движения частицы.

Движение частицы будет выражаться следующим уравнением

(2.23)

где m - масса частицы (кг).

Добавим начальные и граничные условия

Уравнения (2.20), (2.21) и (2.23) позволяют определить характер движения жидкости с примесями. Данные системы решаются с помощью метода конечных элементов. Пример распределения примесей в баке можно видеть на рис 2.7

Рис 2.6 Распределение примесей в баке (v₀=2,358 м/с)

Идея метода конечных элементов состоит в том, что любую непрерывную величину, такую, как температура, давление и перемещение, можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области [9].

В общем случае непрерывная величина заранее неизвестна и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если с начало предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к более общему случаю. Итак, при построении дискретной модели непрерывной величины поступают следующим образом [7]:

·в рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.

·значения непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

·область определения непрерывной величины разбивается на конечное число подобластей называемых элементами. Эти элементы имеют общие узловые точек в совокупности аппроксимируют области.

·непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента (этот полином называется функцией элемента).

Рассмотрим трехмерный элемент, представляющий собой параллелограм. Он имеет четыре узла. Обозначим их индексами i, j, k, l, причем обход узлов в том порядке, как они написаны, осуществляется против часовой стрелки. Интерполяционный многочлен имеет вид:

или в матричном виде:

Коэффициенты (t=1..4) можно определить, используя четыре условия в узлах

где вектор - является вектором значений скалярной функции в соответствующих узлах элемента, то есть - являются числами.

Мы получили систему уравнений 4x4. Запишем эту системы в матричной форме:

где 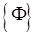- столбец (4x1), [C] - матрица (4x4), - столбец коэффициентов.

Матрица [C] строится для каждого элемента (то есть у каждого элемента своя и зависит от координат узлов конкретного элемента). Запишем матрицу [C]:

Для примера рассмотрим элемент с координатами узлов I=(1,2), J=(2,1), то первые две строки матрицы будут:

Столбец может быть получен, как

но так как нам, то получаем

Но как нам известно представимо в виде:

где строка функций формы. Это выражение можно расписать как:

так как 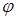одно и тоже, то мы получаем, что:

то есть мы получили аппроксимацию 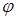по узловым точкам и нам в общем случае необходимо найти обратную матрицу . Обычно обратная матрица находится по правилу Крамера. Если мы найдем обратную матрицу, то сможем записать функции формы элемента:

Примеры разбиения бака и трубопровода на элементы приведены ниже

Рис 2.7 Пример разбиения трубопровода на элементы

Рис 2.8 Пример разбиения бака на элементы

Движение жидкости в трубопроводе аналогично движению в баке-отстойнике, за исключением того, что трубопровод имеет иную геометрию, поэтому будут иные граничные условия. Начальное значение скорости будет вычисляться по формуле (2.22). Как ведут себя примеси в трубопроводе показано на рис 2.8

Рис 2.9 Распределение примесей в трубопроводе

⇐ Предыдущая 1 2 3 456 Следующая ⇒

Воспользуйтесь поиском по сайту: