 |
Понятие интеграла и его свойства
|
|
|
|
Государственное бюджетное профессиональное
Образовательное учреждение
«Пермский агропромышленный техникум»
Реферат (исследование теоретического характера)
По дисциплине «Проектная деятельность»
Тема: Применение интеграла для нахождения площадей объектов ландшафтного дизайна
Выполнила:
Студентка гр. СПЛС 9-16_____________________Скуратович Дарья Сергеевна
Руководитель:___________________________ Лахно Александра Михайловна
Пермь 2017
Содержание:
Введение
1. Теоретические аспекты интегрального исчисления……………………..
1.1. История интегрального исчисления ……………………………………
1.2. Понятие интеграла и его основные свойства…………………………..
1.3. Применение интеграла в математике и физике…………………………
2. Применение для вычисления площадей объектов ландшафтного дизайна..
2.1. Задача на нахождения площадей объектов ландшафтного дизайна ……..
Заключение………………………………………………………………………..
Литературный список…………………………………………………………….
Приложение ………………………………………………………………………
Аннотация
Объект исследования -
Предметом исследования
Цель работы
Задачи:
Актуальность работы
Практическая значимость
Методология работы
Введение
Объект исследования -
Предметом исследования
Цель работы
Задачи:
Актуальность работы
Практическая значимость
Методология работы
Теоретические аспекты интегрального исчисления
История интегрального исчисления
Интегральное исчисление — раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений.
|
|
|
Интеграл (от лат. Integer - целый) - одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.
Символ интеграл введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится, как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования "восстанавливает" функцию, дифференцированием которой получена подынтегральная функция.) Возможно происхождение слова интеграл иное: слово integer означает целый.
В ходе переписки И.Бернулли и Г.Лейбниц согласились с предложением Я.Бернулли. Тогда же, в 1696г., появилось и название новой ветви математики - интегральное исчисление, которое ввел И. Бернулли.
Другие термины, относящиеся к интегральному исчислению, появились значительно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее "примитивная функция", которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как "начальный": F(x)= - начальная (или первоначальная, или первообразная) для функции f(x), которая получается из F(x) дифференцированием.
В современной литературе множество всех первообразных для функции f(x) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную.
Понятие интеграла и его свойства
Первообразной функцией по отношению к данной функции 
называется такая функция 
, производная от которой равна данной функции, т.е. 
|
|
|
Для данной функции 
первообразных функций бесчисленное множество, т.к. любая из функций 
, также является первообразной для 
.
Теорема. Две различные первообразные одной и той же функции, определенной на промежутке,отличаются друг от друга в этом промежутке на постоянное
слагаемое.
Совокупность всех первообразных 
для данной функции 
называется ее неопределенным интегралом обозначается символом:
, где
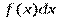называется подынтегральным выражением, функция 
- подынтегральной функцией.
Доказательство: 
Доказательство:
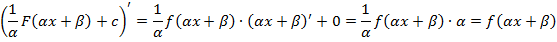
Все формулы интегрирования сохраняют свой вид при замене независимой переменной 
любой непрерывной дифференцируемой функции от .
Смотрите таблицу (Приложение 1)
|
|
|
