 |
Нагружение стойки. Определение тормозного (реактивного) момента
|
|
|
|
Кинематический и силовой расчет многозвенного зубчатого механизма
Исходные данные.
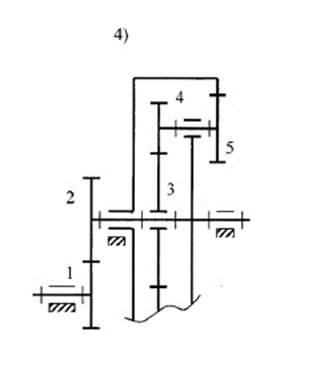
Рис. 1


Частота вращения ведущего звена nвщ = 1000 об/мин.
Момент сопротивления на ведомом валу Мс = 50 Н∙м
Произвести кинематический и силовой расчет многозвенного зубчатого механизма.
Определение неизвестного числа зубьев и количества сателлитов
Ведущее звено – зубчатое колесо 1, ведомое – колесо 3, неподвижное – колесо 6. К колесу 3 приложен момент сопротивления Мс = 50 Н∙м. Частота вращения ведущего колеса: nвщ = 1000 об/мин.
Определим недостающее число зубьев колеса Z6.
Z3 + Z4 = Z6 – Z5;
Z6 = Z3 + Z4 + Z5 = 28 + 24 + 30 = 82
Выберем число сателлитов:
 ,
,
где m – целое число.
Примем n = 5, тогда  ,
, 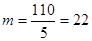
m – целое число, поэтому условие сборки выполняется. Проверим условие соседства.
Для колес 3 и 4:
(Z3 + Z4)·sin (180°/n) > Z4 + 2
(28 + 24)·sin (180°/5) > 24 + 2
30,6 > 26
Для колес 5 и 6:
(Z6 – Z5)·sin (180°/n) > Z5 + 2
(82 – 30)·sin (180°/5) > 30 + 2
30,6 > 32 – неверно. Условие соседства не выполняется.
Примем n = 2, тогда  ,
, 
m – целое число, поэтому условие сборки выполняется. Проверим условие соседства.
Для колес 3 и 4:
(28 + 24)·sin (180°/2) > 24 + 2
52 > 26
Для колес 5 и 6:
(82 – 30)·sin (180°/2) > 30 + 2
52 > 32 – верно.
Условие соседства выполняется.
Определение передаточного отношения
Определим передаточное отношение аналитическим способом. Рассматриваемый механизм состоит из комбинации одной ступени колес с неподвижными осями (1 – 2) и планетарной ступени (5 – 6 – 4 – 3). Общее передаточное отношение равно:
Uобщ = U13 = U12 · UН3(6)



Передаточное отношение меньше единицы, поэтому механизм является мультипликатором. Uобщ < 0, следовательно, ведущее и ведомое колеса вращаются в разные стороны.
|
|
|
Определение радиусов окружностей колес
Вычислим радиусы начальных окружностей всех колес, которые по принятому условию, совпадают с делительными окружностями:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Вычертим в масштабе кинематическую схему механизма.
Определим степень подвижности механизма.
Степень подвижности механизма W определяется по формуле Чебышева:
W = 3n – 2p5 – p4,
где n = 4 – число подвижных звеньев,
p5 = 4 – число кинематических пар V класса (О1, О2, О3, О4),
p4 = 3 – число кинематических пар IV класса (А, В, С).
Получаем: W = 3·4 – 2·4 – 3 = 1, т.е. механизм имеет одно ведущее звено – зубчатое колесо 1.
Силовой расчет
Так как задан момент сопротивления МС, силовой расчет начнем с рассмотрения квазистатического равновесия колеса 3. Покажем его схему нагружения.
К колесу 3 приложен момент сопротивления МС.
Вследствие того, что выбрано два сателлита в точках В, В’ изобразим две силы  со стороны колеса 4 блока сателлитов 4–5, действующих на колесо 3. Эти силы направлены так, чтобы момент, создаваемый ими, уравновесил момент МС.
со стороны колеса 4 блока сателлитов 4–5, действующих на колесо 3. Эти силы направлены так, чтобы момент, создаваемый ими, уравновесил момент МС.
Составим два уравнения.
 ;
;
 ;
;
 .
.
 ;
;
Рассмотрим схему нагружения блока сателлитов 4–5. На блок сателлитов 4–5 действуют силы со стороны колес 3 и 6, а также сила  со стороны водила.
со стороны водила.
Составим два уравнения.
 ;
;
 ;
;
 .
.
 ;
;

Рассмотрим нагружение водила Н и колеса 2. Со стороны блока сателлитов на водило действуют силы  . На колесо 2 со стороны колеса 1 действует сила
. На колесо 2 со стороны колеса 1 действует сила  . Со стороны стойки действует сила
. Со стороны стойки действует сила  .
.
Составим два уравнения.
 ;
;
 ;
;
 .
.

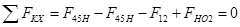 ;
;

Рассмотрим нагружение колеса 1. Со стороны колеса 2 на него действует сила  . Чтобы уравновесить момент от этой силы, к колесу 1 должен быть приложен момент. Это движущий момент Мд. Со стороны стойки действует сила
. Чтобы уравновесить момент от этой силы, к колесу 1 должен быть приложен момент. Это движущий момент Мд. Со стороны стойки действует сила  .
.
Составим два уравнения.
|
|
|
 ;
;
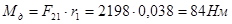 .
.
 ;
;

Проверим правильность проведенных вычислений:
МС = – Мд ∙ Uобщ
50 = 84 ∙ 0,598
50 ≈ 50,2
В пределах погрешности округлений получили тождество. Расчеты проведены, верно.
Нагружение стойки. Определение тормозного (реактивного) момента
В местах крепления колес с неподвижными осями 1 и 2 на корпус через валы колес действуют силы  ,
,  . Кроме того, стойкой является и неподвижное колесо 6, закрепленное на корпусе. На это колесо со стороны колеса 5 действуют силы
. Кроме того, стойкой является и неподвижное колесо 6, закрепленное на корпусе. На это колесо со стороны колеса 5 действуют силы  , которые также будем обозначать
, которые также будем обозначать  .
.

Этих сил две, так как механизм имеет два блока сателлитов. Покажем схему нагружения стойки.
Составим уравнение статики для стойки.
 ;
;

357 – 357 + 2198–2198 = 0
0 = 0
Следовательно, равнодействующая реактивных сил, приложенных к стойке, равна нулю.
Тормозной (реактивный) момент найдем из уравнения моментов.


2·357·0,164 – 2198·(0,038 + 0,076) + МТ = 0
МТ = 134 Н·м
Проверим выполнение равенства:
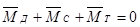 .
.
С учетом направлений моментов получим:
134 – 50 – 84 = 0
0 = 0 – верно.
|
|
|


