 |
Порядок выполнения работы.
|
|
|
|
Экспериментальная установка
Схема установки показана на рисунке 1. Установка состоит из стеклянного сосуда 1, баллона 2 со сжатым воздухом и U- образного жидкостного манометра 3. Имеется также два крана – впускной кран 4, служащий для напуска газа в сосуд 1 из баллона 2, и выпускной кран 5 для соединения сосуда с атмосферой.

Вывод рабочей формулы.
Рассмотрим метод Клемана – Дезорма. Напустим воздух в стеклянный сосуд 1 (см. рисунок) и закроем кран 4. При быстром сжатии температура воздуха повышается. Поэтому после прекращения напуска разность уровней жидкости в манометре будет постепенно уменьшаться, пока температура воздуха внутри сосуда не сравняется с температурой окружающего воздуха. Назовем состояние воздуха в сосуде после выравнивания температур состоянием 1. Параметры состояния 1: V 1 - объем единицы массы воздуха; t 1 - температура воздуха; р1 - давление в сосуде.
Откроем кран 5 и, как только давление в сосуде сравняется с атмосферным, закроем его. Так как расширение происходит очень быстро, то процесс близок к адиабатическому и, следовательно, температура понизится до t 2. Объем единицы массы воздуха станет равным V 2. Воздух, оставшийся в сосуде, перейдет в состояние 2 с параметрами V 2, t 2, р2 (р2 –атмосферное давление). Так как температура t 2 меньше наружной, то воздух в сосуде будет постепенно нагреваться (вследствие теплообмена с окружающей средой) до температуры окружающего воздуха t1. Это нагревание происходит изохорически, так как кран закрыт. Давление воздуха в сосуде увеличивается по сравнению с атмосферным, и в манометре возникает разность уровней h 2, т.е. воздух переходит в состояние 3 с параметрами V 2, t 1, р3.
|
|
|
Таким образом, мы имеем три состояния газа со следующими параметрами:
| Состояние Параметр | |||
| Объем | V 1 | V 2 | V 2 |
| Температура | t 1 | t 2 | t 1 |
| Давление | p 1 | p2 | p 3 |
В состояниях 1 и 3 воздух имеет одинаковую температуру, следовательно, параметры этих состояний можно связать уравнением изотермического процесса (уравнением Бойля – Мариотта):
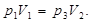 или
или  (4)
(4)
Переход от состояния 1 к состоянию 2 происходит адиабатически, поэтому параметры их связаны уравнением Пуассона (3):
 или
или  . (5)
. (5)
Из уравнений (4) и (5) получим
 (6)
(6)
Прологарифмировав равенство (6), получим
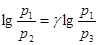 , (7)
, (7)
Если давление измерять жидкостным манометром, то вместо р можно писать соответствующую высоту жидкости. Тогда можно ввести обозначения
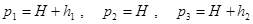
где H – атмосферное давление, h1 – разность уровней манометра в первом состоянии, h2 – разность уровней в третьем состоянии.
Тогда выражение (7) можно переписать в виде
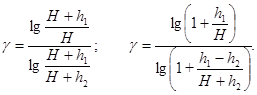
Так как величины h 1 и h 2, выраженные в миллиметрах ртутного столба, очень малы по сравнению с Н и, следовательно, дроби h 1/ H и (h 1 - h 2)/(H + h 2) также незначительны, для нахождения величины логарифма можно воспользоваться приближенным выражением
 ,
,
где х - малая величина.
Поскольку х 2 и, тем более, х 3 - величины высших порядков малости, ими можно пренебречь, тогда lg(1 + x) @ x и, следовательно,

Пренебрегая величиной h 2 в сумме H + h 2, получим расчетную формулу
 . (7)
. (7)
Порядок выполнения работы.
1) открыв кран 4, напустить воздух из баллона 2 в сосуд 1; закрыть кран;
2) подождать, когда разность уровней жидкости в манометре стабилизируется, измерить разность уровней h 1;
3) открыть кран 5, и когда избыток воздуха выйдет из сосуда, быстро закрыть его (в данной работе параметры установки подобраны таким образом, что достаточно повернуть кран 5 на 180° чтобы давление газа в сосуде сравнялось с атмосферным).
4) подождать, когда разность уровней жидкости в манометре стабилизируется (температура воздуха в сосуде станет равной комнатной температуре); измерить разность уровней h 2.
|
|
|
5) повторить пп.1-4 не менее десяти раз (напуская в сосуд воздух до разного давления), по результатам измерений заполните таблицу:
Таблица 1
| Физ. величина | h 1 | Dh1 | h 2 | Dh2 | h 1 - h 2 | g i |
| Ед. измерения Номер опыта | ||||||
| 1. | ||||||
| 2. | ||||||
| … | ||||||
| n |
___________________
Примечание. Dh1 и Dh2 - приборная ошибка в измерении h 1 и h 2. Dh1= Dh2 = 1 мм.
6) вычислить g для каждого измерения по формуле (7); найти среднее значение  ;
;
7) погрешность измерения в этом случае (величина g определяется многократно) допускается рассчитать как среднюю квадратичную для серии n измерений:
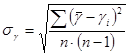 .
.
8) привести окончательный результат.
Контрольные вопросы
1. Что такое теплоемкость, молярная теплоемкость, удельная теплоемкость? Как они связаны? Какова размерность теплоемкости? От чего зависит молярная теплоемкость?
2. Почему Cp > CV с точки зрения первого начала термодинамики?
3. Какой процесс называют адиабатическим? Каким уравнением описывается адиабатический процесс? Изобразите адиабату в координатах p-V.
4. Какие термодинамические процессы происходят в данной работе? Изобразите эти процессы в координатах p-T, V-T, р-V.
5. Почему измерение давления следует производить не сразу после напуска (выпускания) воздуха, а через некоторое время?
|
|
|


