П.1.8 Логарифмирование и потенцирование

МАТЕМАТИЧЕСКИЕ МЕТОДЫ

п.1.1 Векторная величина характеризуются численным значением А (модулем) и направлением (единичный вектор, совпадающий по направлению с вектором ). Поэтому вектор можно представить выражением:

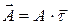
С другой стороны, любой вектор можно выразить через его проекции на координатные оси:

,
где А_х, А_у, А_z – проекции вектора на координатные оси х, у, z;
, , - единичные векторы направлений координатных осей х, у и z.
Проекции вектора на координатные оси х, у, z определяются выражениями:

, ,
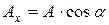где α, β и g – углы между вектором и осями координат х, у и z, соответственно; А – численное значение (модуль) вектора .

Угол между направленными отрезками (векторы, координатные оси) – это угол между концами векторов.

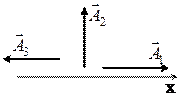В зависимости от значения угла проекция вектора может быть положительной, отрицательной или равна нулю (см.рис):

a = 0⁰ Þ ; a = 90⁰ Þ ;
a = 180⁰ Þ .

п.1.2 Произведение вектора на скаляр k (k > 0, k < 0)

.

Из этого выражения следует:

а) А = ïkï×В;

в) если k > 0, то векторы и совпадают по направлению ( ­­ );

если k < 0, то векторы и антипараллельны ( ­¯ ).

п.1.3 Все действия с векторами (сложение, вычитание, умножение (скалярное, векторное)) можно производить

- геометрически, когда известны модули векторов и их направления (угол между векторами);

- аналитически, когда известны проекции векторов на координатные оси.

п.1.4 Сложение и вычитание векторов
а) геометрически. Пусть заданы векторы и (модули А и В и угол α между векторами) (рис.1.1а). Определим сумму векторов и , то есть модуль и направление вектора = + .
Сложение двух векторов можно производить по правилу «параллелограмма» (рис.1.1б) и по правилу «цепочки» («треугольника») (рис.1.1в)

 

 

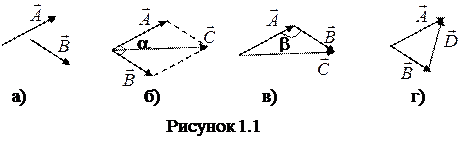
Модуль вектора определятся по теореме косинусов:

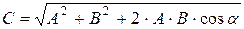или .

Определим разность векторов и , то есть модуль и направление вектора = - . Для этого преобразуем эту разность так, чтобы в уравнении были только положительные слагаемые: + = . В полученном уравнении известны одно из слагаемых и суммарный вектор . Из правила «треугольника» видно (рис.1.1в), что из одной точки выходят два вектора – суммарный вектор и одно из слагаемых . В нашем случае известны суммарный вектор и одно из слагаемых (рис1.1а), поэтому второе слагаемое определяем из векторного треугольника построением (слагаемые выстраиваются в цепочку) (рис.1.1г).

б) аналитически. Пусть задано векторное уравнение . При этом известны проекции векторов , и на координатные оси (А_х, В_х, С_х, А_у, В_у, С_у и т. д..). Необходимо найти вектор - модуль и направление. Из векторной алгебры известно, что

любое векторное уравнение можно выразить в проекциях на координатные оси:

, и т. д.
Тогда 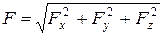, , и т. д.

п.1.5 Скалярное произведение векторов
а) геометрически (известны модули векторов и угол между ними). Скалярное произведение векторов и - это скаляр, определяемый выражением:
,
где α – угол между векторами и ; А_В и В_А – проекция вектора на направление вектора и проекция вектора на направление вектора , соответственно:

, .

б) аналитически (известны проекции векторов 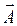и на координатные оси
(А_х, В_х, А_у, В_у и т. д..): .

п.1.6 Векторное произведение векторов
а) геометрически (известны модули векторов и угол между ними). Векторное произведение векторов 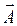и это вектор , модуль которого определяется выражением: .

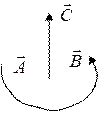Вектор перпендикулярен плоскости, в которой находятся векторы сомножители. Направление вектора определяется по правилу «правого винта»:

- поворачиваем вектор, который слева в произведении (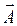) к правому () по кратчайшему пути, этим задавая вращательное движение винта, тогда поступательное движение его показывает направление вектора .

б) аналитически (известны проекции векторов и на координатные оси (А_х, В_х, А_у, В_у и т. д.):

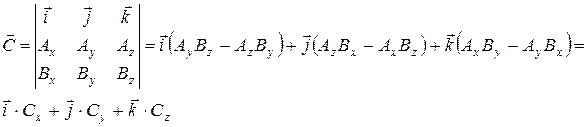
п.1.7 Графики функций

а) линейная функция . График функции – прямая линия (рис.1.2). Слагаемое а – координата у при х = 0. Коэффициент b - тангенс угла наклона a прямой к оси х:

,

где , .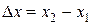

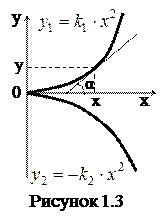б) нелинейная функция, например, . График функции парабола (рис.1.3). Здесь коэффициент k – тангенс угла наклона касательной к кривой в точке с координатами (х,у):

.

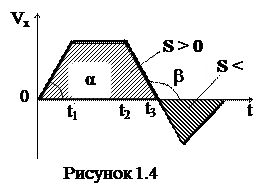в) информация из графиков функций ( на примере графика ):
Пусть задан график А(В). Тогда:

- если или имеет физический смысл (какая-то величина), то эту величину можно найти как тангенс угла наклона кривой. В нашем случае (рис.1.4) или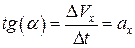

(при а_х = const). Т.о. по графику можно найти а_х – проекцию ускорения на ось х.

- если имеет физический смысл или , то соответствующую физическую величину можно найти как площадь S под кривой. В нашем примере (при V_x = const) или - это проекция перемещения тела на ось х.

п.1.8 Логарифмирование и потенцирование

Логарифмом А числа N при основании а (обозначается ) называется показатель степени, в которую нужно возвысить а, чтобы получить N. Следовательно, из равенства 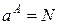следует 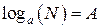, и обратно, из второго равенства вытекает первое.
При основании а = 10 - десятичные логарифмы (lg(N)), при основании е = 2,72 – натуральные логарифмы (ln(N)).Свойства логарифмов приведены в Приложении 1.

Логарифмированием данной величины называется нахождение ее логарифма. Нахождение величины по ее логарифму называется потенцированием:

логарифмирование: .

потенцирование: Þ

п.1.9 Дифференциальные уравнения
Дифференциальные уравнения – это уравнения, содержащие дифференциалы функции (dy) и аргумента (dx). Решить дифференциальное уравнение – это определить функцию у(х). Для решения дифференциального уравнения необходимо задать начальные условия (у = у₀, х = х₀).
Пусть задано дифференциальное уравнение и начальные условия (х₀ и у₀). Последовательность решения:

а) разделяем переменные ;
б) интегрируем левую и правую часть уравнения с учетом начальных условий. В результате получаем искомую функцию у(х):
Þ у(х).

ПРИЛОЖЕНИЯ

Поделиться:

Воспользуйтесь поиском по сайту: