 |
Структурно-алгоритмическая схема САУ
|
|
|
|
Пояснительная записка
По курсовой работе
“Теория Автоматического Регулирования”
Вариант 5
Выполнили студенты:
группы 3023/1
Акимов Д. А.
Беляев Н. А.
Преподаватель:
Попков Е.Н.
Санкт-Петербург
Расчёт параметров звена, эквивалентирующего нагрузку.
Представить нагрузку системы питания в виде звена, для которого входным сигналом является напряжение на зажимах источника питания, а выходным сигналом – указанная регулируемая переменная. Получить описание звена в виде сокращённой записи дифференциального уравнения и передаточной функции. Установить тип звена и рассчитать численные значения параметров
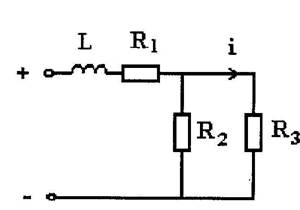
а). Получнение описание звена в виде передаточной функции:
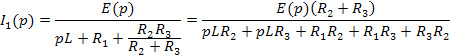
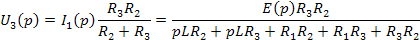
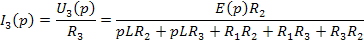

Передаточная функция:
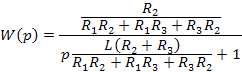
б). Получение описание звена в виде сокращённой записи дифференциального уравнения:
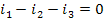
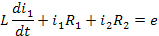


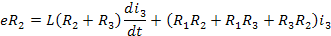
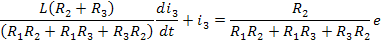
Сокращённая запись дифференциального уравнения:
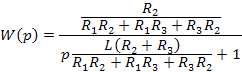
Исходя из полученных результатов и вида W(p), делаем вывод, что исследуемое звено суть инерционное (апериодическое) звено 1-го порядка.

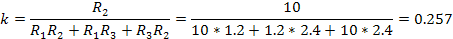

2. Расчёт величины ЭДС Е0 основного источника
Определить двумя способами величину ЭДС основного источника: методом расчета установившегося режима системы питания и нагрузки и используя передаточную функцию звена нагрузки. ЭДС регулируемого источника принять равной нулю.
а) метод расчета установившегося режима системы питания и нагрузки.
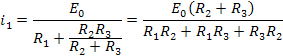
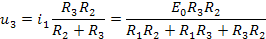
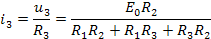
В установившемся режиме по условию 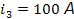

б) Определение Е0 основного источника, используя передаточную функцию звена.
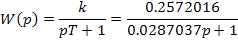
В установившемся режиме по условию 
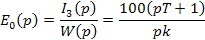
|
|
|
Применим к Е0(р) обратное преобразование Лапласа (здесь и далее все расчёты производились в программе MathCad):
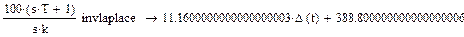
|
Пренебрегая в силу малости первым слагаемым, получаем Е0 = 388.8 В.
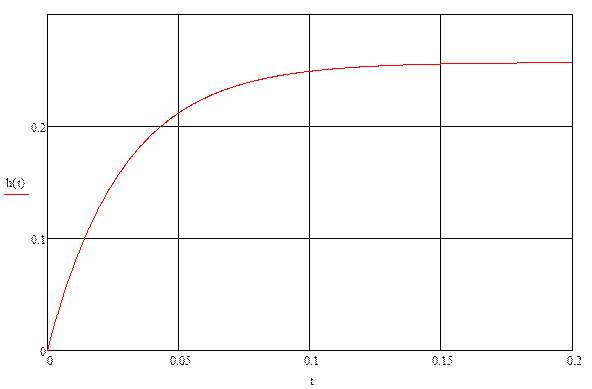
Аналитическая переходная характеристика звена нагрузки
Построить аналитическую переходную характеристику звена, эквивалентирующего нагрузку.
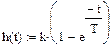
|
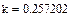
|
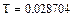
|
|
Опытная переходная характеристика звена нагрузки
Подготовить имитационную модель и получить на ЭВМ переходную характеристику звена, эквивалентирующего нагрузку. Сравнить с результатами п.3. Определить параметры звена по экспериментальной переходной характеристике.
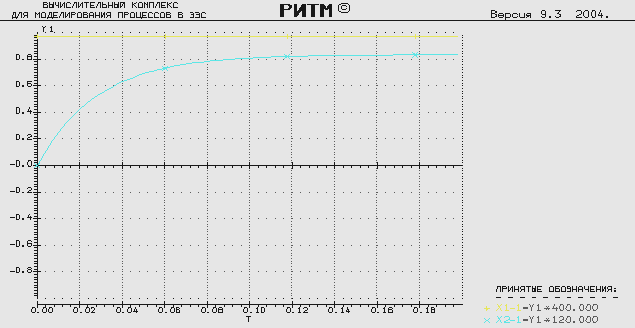
Здесь и далее моделирование процессов производилось в программе РИТМ:
Схема имитационной модели:
 | ||||||
|
|
1) BLT 103 – генератор кусочно-постоянного сигнала
2) BLT 133 – инерционное звено I-ого порядка
3) BLT 014 – осциллограф
4) BLT 015 – табулятор

Здесь:
X1- сигнал на входе звена (единичное ступенчатое воздействие)
X2- сигнал на выходе, который является переходной характеристикой звена (реакция звена на единичное ступенчатое воздействие).
Рассчитанные аналитически параметры:
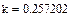
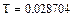
Полученные в РИТМе параметры звена:

|

|
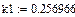
|
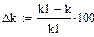
|

|

|
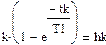
|

|
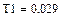
|
|

|

|
Отличие параметров, полученных опытным и аналитическим путём, составляет не более 0.01%. Таким образом, опытная и аналитическая переходные характеристики звена практически совпадают.
Тестовый расчёт
Выполнить тестовый расчёт, подтверждающий правильность определения величины ЭДС Е0.
Включим в цепь вместо источника единичного ступенчатого сигнала источник с найденным аналитическим значением ЭДС. Структурная схема и схема имитационной модели – как в п. 4.
Здесь:
X1- сигнал на входе звена (ЭДС);
|
|
|
X2- сигнал на выходе (регулируемая величина)
При выполнении тестового расчёта было установлено значение ЭДС, равное 388.8 В. Значение полученного выходного сигнала равно 99.91А, что отличается от номинального значения регулируемой величины (100 А) на 0.001%.
Аналитическая АФЧХ
Построить аналитическую амплитудно-фазочастотную характеристику звена, эквивалентирующего нагрузку.
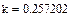
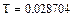
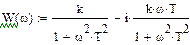
|
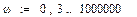
|
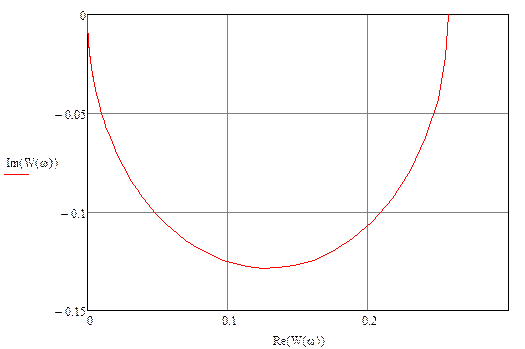
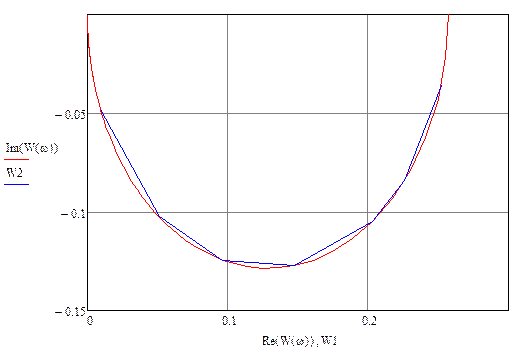
Выберем ряд точек на аналитической АФЧХ (построим ломаную), по которым будем строить экспериментальную АФЧХ:
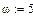
|
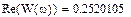
|

|
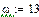
|

|
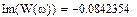
|

|

|
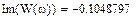
|

|
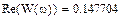
|
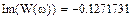
|

|
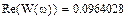
|

|
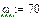
|
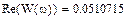
|

|
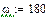
|

|
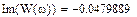
|

|

|
|
Экспериментальная АФЧХ
Подготовить имитационную модель и провести серию расчётов, позволяющую построить экспериментальную амплитудно-фазочастотную характеристику звена, эквивалентирующего нагрузку.
Схема имитационной модели:
 | ||||||
|
| |||||
1) BLT 091 – генератор гармонического сигнала
2) BLT 133 – инерционное звено первого порядка
3) BLT 014 – осциллограф
4) BLT 015 – табулятор
Расчёт параметров серии экспериментов для построения экспериментальной АФЧХ
| Расчётные данные | Опытные данные | ||||||
| ω, рад/с | f, Гц | T, с | Ток. | h | Тга | Xm | φ |
| 0,795775 | 1,256637 | 8,796460 | 0,006283 | 6,283186 | 0,254561 | -0,142521 | |
| 2,069014 | 0,483322 | 3,383254 | 0,002417 | 2,416610 | 0,240943 | -0,357116 | |
| 2,864789 | 0,349066 | 2,443461 | 0,001745 | 1,745329 | 0,228482 | -0,476836 | |
| 4,774648 | 0,209440 | 1,466077 | 0,001047 | 1,047198 | 0,194884 | -0,710851 | |
| 7,161972 | 0,139626 | 0,977384 | 0,000698 | 0,698132 | 0,157448 | -0,911904 | |
| 11,140845 | 0,089760 | 0,628319 | 0,000449 | 0,448799 | 0,114596 | -1,108940 | |
| 28,647887 | 0,034907 | 0,244346 | 0,000175 | 0,174533 | 0,048874 | -1,378970 |
Пример расчёта (2-я строка):
f = ω/2π = 13 рад/с /2π = 2,069014 Гц
Т = 1/f = 1/2,069014 Гц = 0,483322 с
Ток. = 7Т = 7*0,483322 с = 3,383254 с
h = Т/200 = 0,483322 с / 200 = 0,002417 с
Тга = 5Т = 5*0,483322 с = 2,416610 с
Tок – время окончания расчета,
Тга – время гармонического анализа,
h – шаг расчета.
Осциллограмма входного и выходного сигнала при частоте ω = 45 рад/с
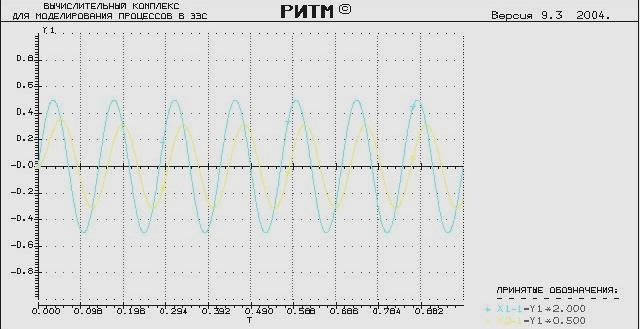
Здесь:
Х1 – входной сигнал (ЭДС)
Х2 – выходной сигнал (регулируемая величина)
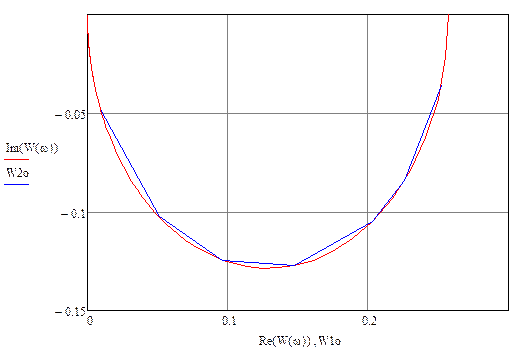
Полученная экспериментально АФЧХ совпадает с аналитической:
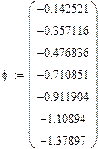
|
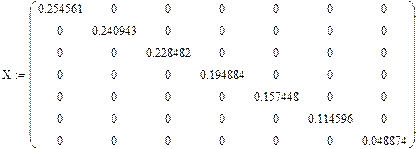
|
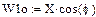
|
|
|
|
|
|
Структурно-алгоритмическая схема САУ
Составить структурно-алгоритмическую схему системы автоматического управления
 | |||||||
 | |||||||
| |||||||
 |







 |
После преобразования:
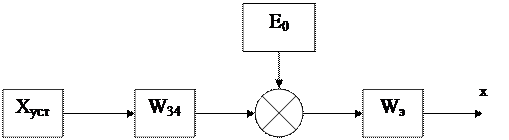
где: 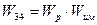

Полученное значение передаточной функции эквивалентированной структурно – алгоритмической схемы САУ имеет вид:
а). относительно источника ЭДС Е0: 
б). относительно сигнала уставки: 
9. Построение области устойчивости системы в плоскости коэффициентов Кр и Кд
Построить область устойчивости системы в плоскости коэффициентов Кр и Кд, где
Кр —коэффициент передачи звена, эквивалентирующего регулятор
Кд — коэффициент передачи звена, эквивалентирующего датчик текущего значения регулируемой переменной
Полученное значение передаточной функции эквивалентированной структурно – алгоритмической схемы САУ:
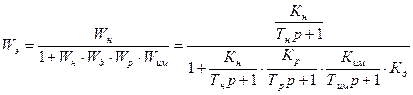

Характеристическое уравнение найдем, приравняв к нулю знаменатель передаточной функции:  D(λ) = R(λ)
D(λ) = R(λ)
Отсюда характеристическое уравнение будет иметь вид:
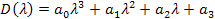
При подстановке известных характеристик элементов цепи регулирования получим:
a0 = 287; a1 = 27.22*103; a2 = 82.96*104; a3 = 4.1152*106 Кр Кд+8*106
Условия нарушения устойчивости:
1). появление нулевого корня
2). выход пары комплексных корней на мнимую ось
По 1-му условию имеем:
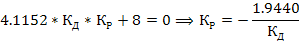
Граница области устойчивости для 2-го условия рассчитывается исходя из равенства нулю предпоследнего минора (Δn-1 = 0) определителя Гурвица.
Составим определитель Гурвица:
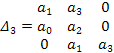
Предпоследний минор:
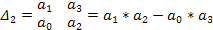
Приравняв полученное выражение к нулю, получим:
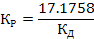
На основе полученных уравнений строим области устойчивости:

1 2 3
4 5
Проверим, какие из этих областей являются устойчивыми. Для этого выберем точку в каждой из областей и воспользуемся критерием Гурвица. Для устойчивости системы необходима и достаточна положительность определителя Гурвица и всех его миноров.
|
|
|
Область 1:
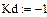
|
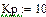
|
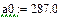
|
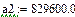
|

|
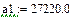
|
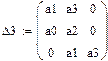
|
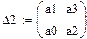
|

|
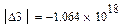
|
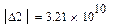
|
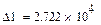
|
Область неустойчива.
Область 2:
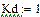
|
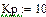
|
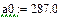
|
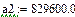
|
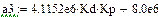
|
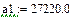
|
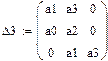
|
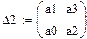
|
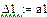
|
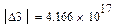
|
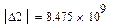
|
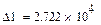
|
Область устойчива
Область 3:
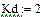
|
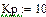
|
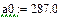
|
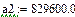
|
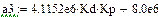
|
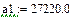
|
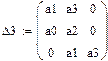
|
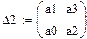
|
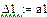
|

|
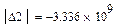
|
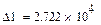
|
Область неустойчива
Область 4:
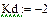
|
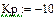
|
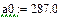
|
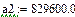
|
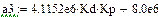
|
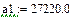
|
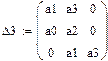
|
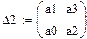
|
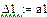
|

|
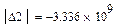
|
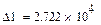
|
Область неустойчива
Область 5:
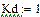
|
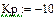
|
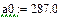
|
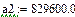
|
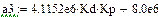
|
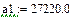
|
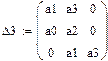
|
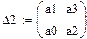
|
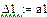
|
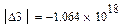
|
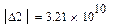
|
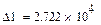
|
Область неустойчива
Таким образом, область 2 является единственной областью устойчивости для данной САУ.
|
|
|


