 |
Разработка алгоритма распознавания линий и расчет их радиальных и тангенциальных составляющих
|
|
|
|
В процессе считывания и преобразования в цифровой массив изображение подвергается различным искажениям и зашумлению, что требует применения средств для его улучшения и реставрации.
Весь алгоритм можно разбить на несколько этапов:
) Ввод изображения.
) Предварительная обработка.
) Распознавание линий.
) Расчет их радиальных и тангенциальных составляющих
) Вывод результата.
Ввод изображения будет осуществляться по средствам захвата с оптического устройства (камеры) либо считывания уже имеющегося.
Предварительная обработка направлена на улучшение изображения, отсечение лишней информации и состоит из нескольких шагов:
) Преобразование в полутоновое изображение.
Так как цвет не несет для нас значимой информации, можно перевести его в полутоновое, заменив значения RGB для каждого элемента матриц на значение интенсивности яркости. Это ускорит процесс обработки, так как программе или функции, работающий с матрицей изображения, необходимо будет оперировать с одним значением для каждого элемента.
) Выравнивание освещения (компенсация разности освещения).
Большинство изображений фаций имеет неравномерное освещение, что вызывает проблемы в процессе дальнейшей обработки. Компенсацию разности будем производить с помощью алгоритма Single scale retinex (SSR).
Принцип работы данного алгоритма:
Исходное изображение 
(рис.2)
Получаем приближенное изображение освещения путем низкочастотной фильтрации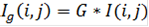 
(рис.3)- матрица свертки низкочастотного фильтра
Восстановим изображение по формуле 
(рис.4)
) Сглаживающая фильтрация (устранение шумов).
Как правило, фильтрация осуществляется путем свертки матрицы изображения с маской, представляющей фильтр. В нашем случае будем использовать фильтр Гаусса. Фильтр Гаусса является результатом операции размытия изображения функцией Гаусса. Данный подход широко применяется в графических редакторах, как правило, для уменьшения зашумленности изображения и сглаживания резких краев. Также Гауссово сглаживание используется в качестве оператора этапа предварительной обработки во многих системах распознавания образов.
|
|
|
С точки зрения математики, применение фильтра Гаусса равносильно свертке изображения с функцией Гаусса (также данный подход известен как двумерное преобразование Вейерштрасса). Механизм работы фильтра заключается в расчете функции Гаусса для каждого пикселя изображения. Уравнение гауссовой функции для одного измерения имеет следующий вид:
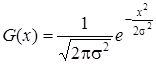, (1)
где x - координата объекта в одномерном пространстве;
σ - среднеквадратичное гауссово отклонение.
В двумерном случае дважды осуществляется расчет функции Гаусса (1) для каждого из измерений:
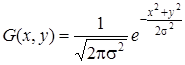, (2)
где x,y - координаты объекта в двумерном пространстве;
σ - среднеквадратичное гауссово отклонение.
Формула (2) дает поверхность, ограниченную концентрическими окружностями, распределенными относительно центральной точки по Гауссу. Значения, вычисляемые на основе этого распределения, используются для построения конволюционной матрицы, которая применяется к исходному изображению.
1) Выделение краев.
Выделение краев будет осуществляться детектором границ Канни. Его преимущества перед остальными детекторами:
а) Хорошее обнаружение, т.е. минимальная вероятность пропуска реального перепада яркости и минимальная вероятность ложного определения перепада (максимизирование выходного отношения сигнал/шум).
б) Хорошая локализация (пиксели, определенные как пиксели края, должны располагаться насколько возможно ближе к центру истинного края).
|
|
|
в) Только один отклик на один край.
Вышеперечисленные критерии были записаны в виде уравнений, которые были решены численно, и был определен путем моделирования вид оптимального (в смысле указанных выше критериев) оператора выделения края.
Принцип работы детектора:
. Свертка изображения с ядром - производной от фильтра гаусса.
. Поиск значения и направления градиента.
. Выделение локальных максимумов.
Утоньшение полос в несколько пикселей до одного пикселя.
. Связывание краев и обрезание по порогу.
Определяем два порога: нижний и верхний
Верхний порог используем для инициализации кривых
Нижний порог используем для продолжения кривых
Пример работы детектора границ Канни представлен в виде исходного изображения (рис.6) и обработанного изображения (рис.7)
Процесс распознавания лини и расчет их радиальных и тангенциальных составляющих можно объединить в одну операцию. Для этого разделим изображение кристаллограммы на несколько сегментов (рис.8). В пределах каждого сегмента ведем радиус с заданным углом смещения, если на его пути будет встречаться линия, проецируем её на радиус и нормаль к нему, поворачиваем радиус на заданный угол и повторяем операцию.
Проекция на радиус будет представлять собой радиальную составляющую линии, а проекция на нормаль - тангенциальную.
|
|
|
