 |
Задание 1.Решение системы линейных уравнений методом Крамера
|
|
|
|
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
3. Сделайте выводы по результатам работы
Вариант№1
Задание 1.Решение системы линейных уравнений методом Крамера
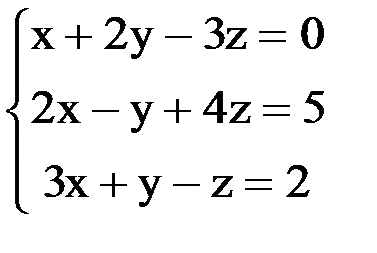
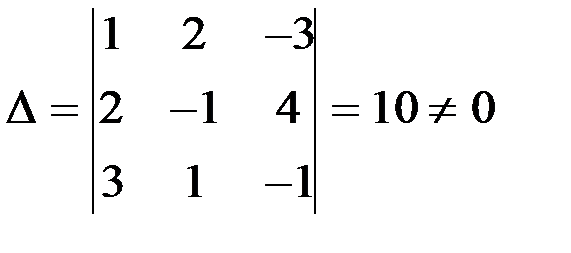

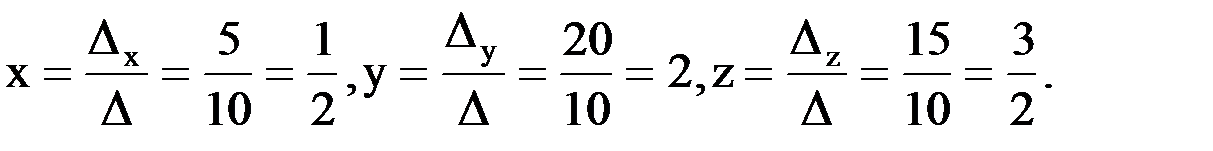
Проверка:
 Ответ: x=0,5; y=2; z=1,5.
Ответ: x=0,5; y=2; z=1,5.
Задание 2. Решить методом Гаусса систему уравнений
x1 – 2x2 + x3 + x4 = –1;
3x1 + 2x2 – 3x3 – 4x4 = 2;
2x1 – x2 + 2x3 – 3x4 = 9;
x1 + 3x2 – 3x3 – x4 = –1.
Решение:Составим матрицу В и преобразуем ее. Для удобства вычислений отделимвертикальной чертой столбец, состоящий из свободных членов:
1 –2 1 1 –1
B = 3 2 –3 –4 2
2 –1 2 –3 9
1 3 –3 –1 –1
Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу,эквивалентную исходной:
1 –2 1 1 –1
0 8 –6 –7 5
0 3 0 –5 11
0 5 –4 –2 0
Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
1 –2 1 1 –1
0 –1 –6 8 –28
0 0 –1 0 –3
0 0 0 19 –19
Из коэффициентов последней матрицы составим систему, равносильную исходной:
x1 – 2x2 + x3 + x4 = –1;
– X2 – 6x3 + 8x4 = –28;
– x3 = –3;
19x4 = –19.
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x4 = –1, из третьего х3 = 3. Подставив значения х3 и x4 во второе уравнение, найдем x2 = 2. Подставив значения x2, x3, x4 в первое уравнение, найдем x1 = 1.
|
|
|
Ответ. (1; 2; 3;-1).
Задание 3. Решить систему уравнений методом обратной матрицы.
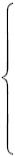
| 2 x1 | + | 3 x2 | = | ||
| - 2 x1 | + | x2 | = |
Решение:
Введем обозначения:
| A = | 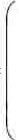
| 
| - матрица А состоит из коэффициентов системы. | ||
| -2 |
| X = | 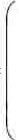
| x 1 | 
| - матрица X состоит из переменных, которые необходимо найти. |
| x 2 |
| B = | 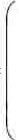
| 
| - матрица B состоит из столбца свободных членов. | |
| E = | 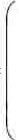
| 
| - единичная матрица. | ||
Теперь исходную систему уравнений можно записать в виде матричного уравнения.
A * X = B
Умножим (слева) левую и правую часть уравнения на A-1 - матрицу обратную матрице A.
A -1 * A * X = A -1 * B
Согласно определению обратной матрицы: A -1 * A = E
E * X = A -1 * B
Согласно определению единичной матрицы: E * X = X
X = A -1 * B
задача сводится к нахождению обратной матрицы A -1
| * |
|
| X = A -1 * B = 1 / 8 * | 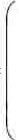
| -11 | 
|
| X = | 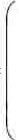
| -11/8 | 
|
| 9/4 |
Ответ:
x1 = -11/8
x2 = 9/4
Задание 4. Сложить и умножить комплексные числа  и
и 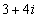 .
.
Решение. Для сложения чисел производим следующие вычисления:

Теперь умножаем:
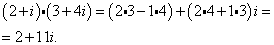
Ответ.5+5i, 2+11i
Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
|
|
|
Порядок выполнения работы:
1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
3. Сделайте выводы по результатам работы
Вариант№2
Задание 1. Решить систему линейных уравнений методом Крамера:
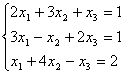 .
.
Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители



По формулам Крамера находим:
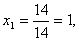

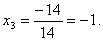
Итак, (1; 0; -1) – единственное решение системы.
Задание 2. Решить систему линейных уравнений методом Гаусса
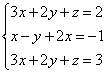
составим расширенную матрицу системы:

переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
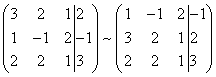
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую, умноженную на на 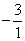 , к третьей – первую строку, умноженную на (в
, к третьей – первую строку, умноженную на (в  .
.
.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:

Для упрощения второй строки полученной системы умножим её на  и получим вновь матрицу системы уравнений, эквивалентной данной системе:
и получим вновь матрицу системы уравнений, эквивалентной данной системе:
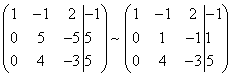
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую, умноженную на на  .
.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

получили эквивалентную данной трапециевидную систему линейных уравнений:

из последнего уравнения определим z:
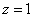 .
.
Подставив это значение в предшествующее уравнение, найдём y:

Из первого уравнения найдём x:

Итак, решение данной системы -  .
.
Задание 3. Решить систему уравнений методом обратной матрицы

Матрица коэффициентов при неизвестных:
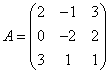
Матрица неизвестных:
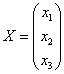
Матрица свободных членов:
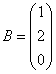
Находим матрицу, обратную матрице коэффициентов при неизвестных:
|
|
|
 .
.
Находим матрицу неизвестных:
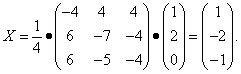
Итак, получили решение:
 .
.
Сделаем проверку:
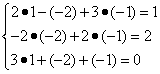
Следовательно, ответ правильный.
Задание 4. Разделить комплексное число 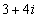 на комплексное число
на комплексное число  .
.
Решение. Умножив числитель и знаменатель дроби  на
на 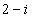 , получаем:
, получаем:

Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
3. Сделайте выводы по результатам работы
Вариант№3
Задание 1. Решить систему линейных уравнений методом Крамера:
 .
.
Решение. Находим определитель системы:
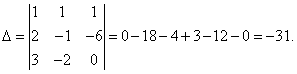
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

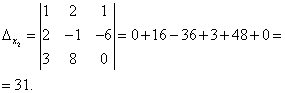

По формулам Крамера находим:

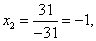
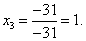
Итак, решение системы - (2; -1; 1).
Задание 2. Решить систему уравнений
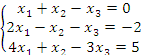
методом Гаусса.
Решение. Преобразуем расширенную матрицу, производя элементарные операции над строками:
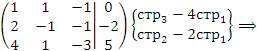
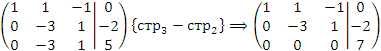
Третья строка этой матрицы соответствует уравнению

не имеющему решений и, следовательно, система является несовместной.
Задание 3. Решить систему уравнений методом обратной матрицы
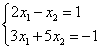
Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
|
|
|

Матрица неизвестных:
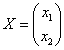
Матрица свободных членов:


Находим матрицу, обратную матрице коэффициентов при неизвестных:
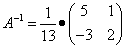 .
.
Находим матрицу неизвестных:
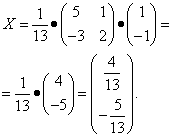
Итак, получили решение:
 .
.
Сделаем проверку:
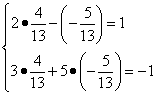
Следовательно, ответ правильный.
Задание 4. Разделить комплексное число 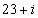 на комплексное число
на комплексное число 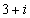 .
.
Решение. Умножив числитель и знаменатель дроби 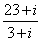 на
на  , получаем:
, получаем:

Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
3. Сделайте выводы по результатам работы
Вариант№4
Задание 1. Решить систему линейных уравнений методом Крамера:
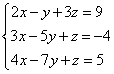
Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
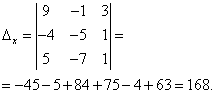
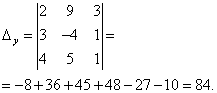
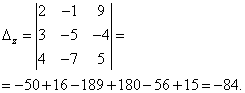
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Задание 2. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.
Решение. Составляем систему линейных уравнений:
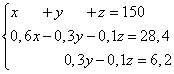
Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:
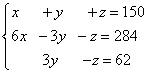
Составляем расширенную матрицу системы:
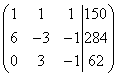
Путём сложения (в нашем случае - вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:
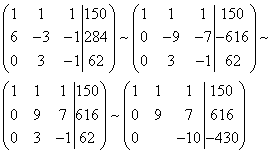
Получили расширенную матрицу трапециевидной формы.
Видим, что  .
.
Из второго уравнения находим
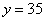 ,
,
Из третьего уравнения -
 .
.
Задание 3. Решить систему уравнений методом обратной матрицы
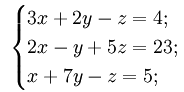
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
|
|
|
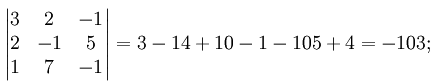
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
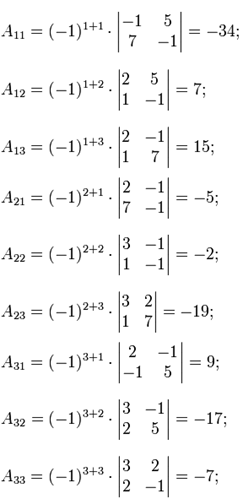
Теперь найдём союзную матрицу и транспонируем её, потом подставим в формулу для нахождения обратной матрицы.
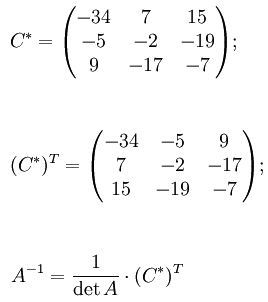
Подставляя переменные в формулу, получаем:

Найдем неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.
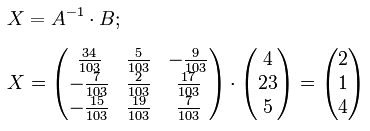
Итак, x=2; y=1; z=4.
Задание 4. Найти x и y, считая их вещественными, в уравнении
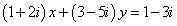 .
.
Решение. Раскрываем скобки:
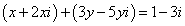 .
.
записываем отдельно действительную и мнимую части:
 .
.
Решаем отдельно уравнение для действительной части и для мнимой части. То есть записываем систему уравнений:
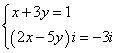
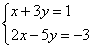
Из первого уравнения выражаем икс и подставляем во второго уравнение:

Находим икс и игрек - получаем решение задачи:

Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
3. Сделайте выводы по результатам работы
Вариант№5
Задание 1. Решить систему линейных уравнений методом Крамера:
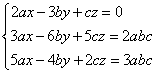
Решение. Находим определитель системы:
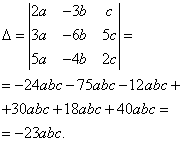
Находим определители при неизвестных
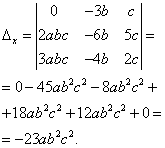
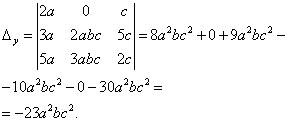
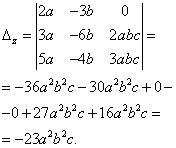
По формулам Крамера находим:
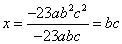 ,
,
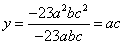 ,
,
 .
.
Задание 2. Решить систему уравнений

методом Гаусса.
Решение. Рассмотрим расширенную матрицу и приведем ее к треугольному виду, выполняя операции над строками:
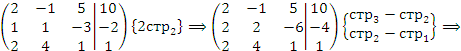

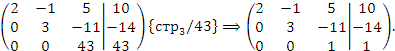
Полученная матрица описывает систему уравнений
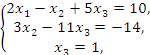
эквивалентную исходной системе. Решение находится элементарно:
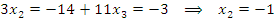
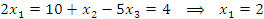
Убедимся в том, что полученный набор 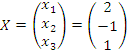 обращает каждое уравнение данной системы в тождество:
обращает каждое уравнение данной системы в тождество:

Задание 3. Решить систему уравнений методом обратной матрицы
x1 - x2 + x3 = 6,
2x1 + x2 + x3 = 3,
x1 + x2 +2x3 = 5.
Решение. Обозначим
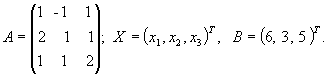
Тогда данная система уравнений запишется матричным уравнением AX=B. Поскольку 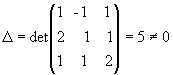 , то матрица A невырождена и поэтому имеет обратную:
, то матрица A невырождена и поэтому имеет обратную:
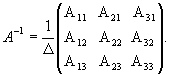 .
.
Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A-1B. В данном случае
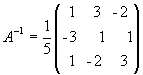
и, следовательно,
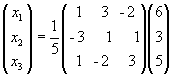 .
.
Выполняя действия над матрицами, получим:
x1 = 1/5(1×6+3×3-2×5) = 1/5 (6+9-10) = 1,
x2 = 1/5 (-3×6 +1×3 - 1×5) = 1/5 (- 18 + 3 + 5) = -2,
x3 = 1/5 (1×6 - 2×3 + 3×5) = 1/5 (6 -6 + 15) = 3.
Итак, X = (1, -2, 3)
Задание 4. Выполнить операцию умножения комплексных чисел 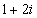 и
и  .
.
Решение. Применяем формулу для умножения и получаем:
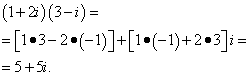
Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
4. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
5. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
6. Сделайте выводы по результатам работы
Вариант№6
Задание 1.Решение системы линейных уравнений методом Крамера
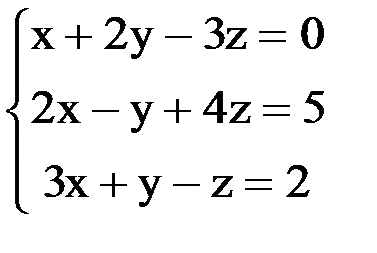
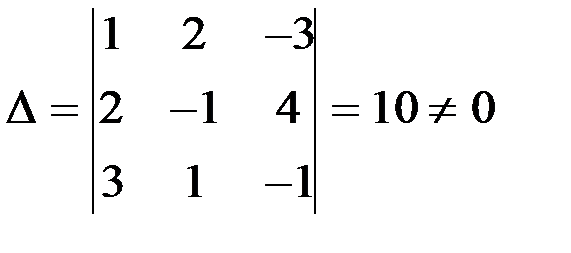

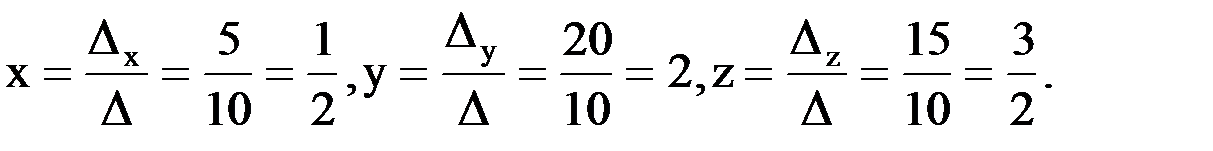
Проверка:
 Ответ: x=0,5; y=2; z=1,5.
Ответ: x=0,5; y=2; z=1,5.
Задание 2. Решить методом Гаусса систему уравнений
x1 – 2x2 + x3 + x4 = –1;
3x1 + 2x2 – 3x3 – 4x4 = 2;
2x1 – x2 + 2x3 – 3x4 = 9;
x1 + 3x2 – 3x3 – x4 = –1.
Решение:Составим матрицу В и преобразуем ее. Для удобства вычислений отделимвертикальной чертой столбец, состоящий из свободных членов:
1 –2 1 1 –1
B = 3 2 –3 –4 2
2 –1 2 –3 9
1 3 –3 –1 –1
Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу,эквивалентную исходной:
1 –2 1 1 –1
0 8 –6 –7 5
0 3 0 –5 11
0 5 –4 –2 0
Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
1 –2 1 1 –1
0 –1 –6 8 –28
0 0 –1 0 –3
0 0 0 19 –19
Из коэффициентов последней матрицы составим систему, равносильную исходной:
x1 – 2x2 + x3 + x4 = –1;
– X2 – 6x3 + 8x4 = –28;
– x3 = –3;
19x4 = –19.
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x4 = –1, из третьего х3 = 3. Подставив значения х3 и x4 во второе уравнение, найдем x2 = 2. Подставив значения x2, x3, x4 в первое уравнение, найдем x1 = 1.
Ответ. (1; 2; 3;-1).
Задание 3. Решить систему уравнений методом обратной матрицы.
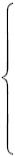
| 2 x1 | + | 3 x2 | = | ||
| - 2 x1 | + | x2 | = |
Решение:
Введем обозначения:
| A = | 
| 
| - матрица А состоит из коэффициентов системы. | ||
| -2 |
| X = | 
| x 1 | 
| - матрица X состоит из переменных, которые необходимо найти. |
| x 2 |
| B = | 
| 
| - матрица B состоит из столбца свободных членов. | |
| E = | 
| 
| - единичная матрица. | ||
Теперь исходную систему уравнений можно записать в виде матричного уравнения.
A * X = B
Умножим (слева) левую и правую часть уравнения на A-1 - матрицу обратную матрице A.
A -1 * A * X = A -1 * B
Согласно определению обратной матрицы: A -1 * A = E
E * X = A -1 * B
Согласно определению единичной матрицы: E * X = X
X = A -1 * B
задача сводится к нахождению обратной матрицы A -1
| * |
|
| X = A -1 * B = 1 / 8 * | 
| -11 | 
|
| X = | 
| -11/8 | 
|
| 9/4 |
Ответ:
x1 = -11/8
x2 = 9/4
Задание 4. Сложить и умножить комплексные числа  и
и 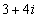 .
.
Решение. Для сложения чисел производим следующие вычисления:

Теперь умножаем:
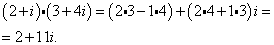
Ответ.5+5i, 2+11i
Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
4. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
5. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
6. Сделайте выводы по результатам работы
Вариант№7
Задание 1. Решить систему линейных уравнений методом Крамера:
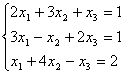 .
.
Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители



По формулам Крамера находим:
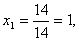

Итак, (1; 0; -1) – единственное решение системы.
Задание 2. Решить систему линейных уравнений методом Гаусса
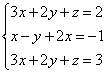
составим расширенную матрицу системы:

переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
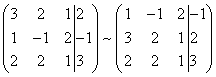
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую, умноженную на на 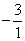 , к третьей – первую строку, умноженную на (в
, к третьей – первую строку, умноженную на (в  .
.
.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:

Для упрощения второй строки полученной системы умножим её на  и получим вновь матрицу системы уравнений, эквивалентной данной системе:
и получим вновь матрицу системы уравнений, эквивалентной данной системе:
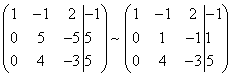
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую, умноженную на на  .
.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

получили эквивалентную данной трапециевидную систему линейных уравнений:

из последнего уравнения определим z:
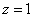 .
.
Подставив это значение в предшествующее уравнение, найдём y:

Из первого уравнения найдём x:

Итак, решение данной системы -  .
.
Задание 3. Решить систему уравнений методом обратной матрицы

Матрица коэффициентов при неизвестных:
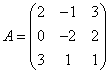
Матрица неизвестных:
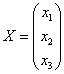
Матрица свободных членов:
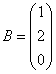
Находим матрицу, обратную матрице коэффициентов при неизвестных:
 .
.
Находим матрицу неизвестных:
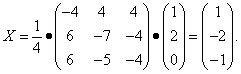
Итак, получили решение:
 .
.
Сделаем проверку:
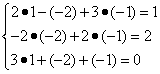
Следовательно, ответ правильный.
Задание 4. Разделить комплексное число 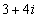 на комплексное число
на комплексное число  .
.
Решение. Умножив числитель и знаменатель дроби  на
на 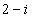 , получаем:
, получаем:

Вывод. В процессе выполнения данной работы я научился решать системы линейных уравнений различными методами и освоил правила выполнения арифметических действий с комплексными числами.
Практическая работа № 1
Тема. Решение систем линейных уравнений с тремя неизвестными методами Крамера, Гаусса, обратной матрицы. Действия с комплексными числами.
Цель работы:
Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
Порядок выполнения работы:
4. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
5. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
6. Сделайте выводы по результатам работы
Вариант№8
Задание 1. Решить систему линейных уравнений методом Крамера:
 .
.
Решение. Находим определитель системы:
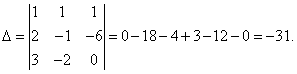
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

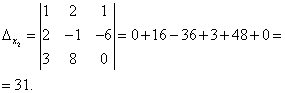

По формулам Крамера находим:


