 |
Геометрический метод решение задач ЛП
|
|
|
|
Задача 1. При откорме каждое животное должно получить не менее 14 ед.питательного вещества S1, не менее 15 ед. вещества S2 и не менее 10 вещества S3. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 килограмме каждого вида корма и стоимость одного килограмма корма дана в таблице 1.
Таблица 1
| Питательные вещества | Количество единиц питательных веществ в 1 кг. корма | |
| корм 1 | корм 2 | |
| S1 | 1 | 2 |
| S2 | 1 | 3 |
| S3 | 2 | 1 |
| Стоимость 1 кг. корма | 3 | 7 |
Составить рацион минимальной стоимости.
Решение:
X1 + 2X2 ≥ 14
X1 + 3X2 ≥ 15
2X1 + X2 ≥ 10
X1, X2 ≥ 0
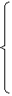3X1 + 7 X2 → min
X1 + 2X2 = 14
X1 + 3X2 =15
2X1 + X2 = 10
Симплексный метод решения задач ЛП
Задача 2. Для изготовления 4-ёх видов продукции P1, P2, P3, P4 используют два вида сырья: S1 и S2. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 2.
Таблица 2.
| Вид сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |||
| P1 | P2 | P3 | P4 | ||
| S1 | 3 | 1 | 1 | 1 | 2 |
| S2 | 7 | 1 | 2 | 3 | 1 |
| Прибыль от единицы продукции | 9 | 14 | 15 | 10 | |
Составить план производства, обеспечивающий получений максимальной прибыли.
Решение:
1. Формальная постановка задачи имеет следующий вид:
9X1 + 14X2 + 15 X3 + 10X4 → max
X1 + X2 + X3 + 2X4 ≤ 3
X1 + 2X2 + 3X3 + X4 ≤ 7
X1, X2, X3, X4 ≥ 0
2. Приведем к стандартной (канонической) форме:
F = 9X1 + 14X2 +15X3 + 10X4 + 0X5 + 0X6
X1 + X2 + X3 + 2X4 + X5 = 3
X1 + 2X2 +3X3 + X4 + X6 = 7
X1, X2, X3, X4 ≥ 0
3. Запишем систему ограничений в векторной форме:
X1 (1/1) + X2 (1/2) + X3 (1/3) + X4 (2/1) + X5 (1/0) + X6 (0/1) = (3/7)
P1 P2 P3 P4 P5 P6 P0
P5, P6 - базисные
|
|
|
4. Запишем первоначальный опорный план:
Х0 (0, 0, 0, 0, 3,7), F0 = 9*0 + 14*0 +15*0 +10*0 + 0*3 +0*7 = 0
Составим соответствующую плану 1 симплексную таблицу:
| Базис | Сб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 |
| 9 | 14 | 15 | 10 | 0 | 0 | |||
| Р5 | 0 | 3 | 1 | 1 | 1 | 2 | 1 | 0 |
| Р6 | 0 | 7 | 1 | 2 | 3 | 1 | 0 | 1 |
|
| -9 | -14 | -15 | -10 | 0 | 0 | ||
Вычислим оценки:
∆ = (Сб*А) - С
∆1 = (0 *1 + 0*1) - 9 = - 9; ∆2 = (0 *1 + 0*2) - 14 = - 14; ∆3 = (0 *1 + 0*3) - 15 = - 15; ∆4 = (0 *2 + 0*1) - 10 = - 10; ∆5 = (0 *1 + 0*0) - 0 = 0; ∆6 = (0 *0 + 0*1) - 0 = 0
Критерием оптимальности является условие, что все ∆ ≥ 0, т.к. это не так, решение не оптимально.
Выберем вектор, который будем включать в базис:
min1 = (3/1; 7/1) = 3; min2 = (3/1; 7/2) =3; min3 = (3/1; 7/3) = 2 1/3; min4 = (3/2; 7/1) = 1 1/2,
теперь посмотрим соотношение min c ∆:
∆ f = - ∆* min
∆ f 1 = - (-9) *3 = 27; ∆ f 2 = - (-14) *3 = 42; ∆ f 3 = - (-15) *2 1/3 = 34.95; ∆ f 4 = - (-10) *1 1/2 = 15,
Отсюда следует, что менять будем Р5 на Р2.
5. Составим 2 симплексную таблицу:
| Базис | Сб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 |
| 9 | 14 | 15 | 10 | 0 | 0 | |||
| Р2 | 14 | 3 | 1 | 1 | 1 | 2 | 1 | 0 |
| Р6 | 0 | 1 | -1 | 0 | 1 | -1 | -1 | 1 |
|
| 5 | 0 | -1 | 4 | 14 | 0 | ||
7- (3*2) /1 = 1; 1 - (1*2) /1 = - 1; 3 - (2*1) /1 = 1; 1- (2*1) /1 = - 1; 0- (1*1) /1 = - 1; 1- (0*1) /1 = 1
∆1 = 14*1+0* (-1) - 9 = 5; ∆ 3 = 14*1+0*1-15 = - 1; ∆ 4 = 14*2+0* (-1) - 10 = 4;
∆ 5 = 14*1+0* (-1) - 0 = 14; ∆ 6 = 14*0+0*1-0 = 0;
Х1 (0,3,0,0,0,1); F1 = 9*0+14*3+15*0+10*0+0*0+0*1 = 42
Приняв этот план видим, что выпуск 2го вида продукции является наиболее выгодным, остаток сырья 2го вида продукции составит 1 единица.
Т.к. не все ∆ ≥ 0, план не является оптимальным, поэтому продолжим…..
Вектором Р3 заменим Р6 min = (3/1, 1/1) = (3,1)
6. Составим 3 симплексную таблицу
| Базис | Сб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 |
| 9 | 14 | 15 | 10 | 0 | 0 | |||
| Р2 | 14 | 2 | 2 | 1 | 0 | 3 | 2 | -1 |
| Р3 | 15 | 1 | -1 | 0 | 1 | -1 | -1 | 1 |
|
| 4 | 0 | 0 | 17 | 13 | 1 | ||
3-1*1/1=2; 1- (-1) *1/1=2; 1-0*1/1=1; 2-1* (-1) /1=3; 1-1* (-1) /1=2; 0-1*1/1=-1
∆1 = 14*2+15* (-1) - 9 = 4; ∆ 2 = 14*1+15*0-14 = 0; ∆ 4 = 14*3+15* (-1) - 10 = 17;
∆ 5 = 14*2+15* (-1) - 0 = 13; ∆ 6 = 14* (-1) +15*1-0 = 1;
Х2 = (0,2,1,0,0,0); F2 = 9*0+14*2+15*1+0 = 43
План является оптимальным, говорим о том, что наиболее выгодным является производство 2единиц 2 вида продукции и 1единицы 3 вида продукции, причем сырье расходуется полностью.
|
|
|
Теоремы двойственности и их использование в задачах ЛП
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей, как мы уже знаем, в нахождении максимального значения функции
(42)
при условиях
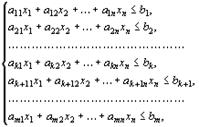(43)
(44)
Определение.
Задача, состоящая в нахождении минимального значения функции
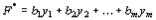(45)
при условиях
(46)
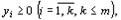(47)
называется двойственной по отношению к задаче (42) - (44). Задачи (42) - (44) и (45) - (47) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:
1. Целевая функция исходной задачи (42) - (44) задается на максимум, а целевая функция двойственной (45) - (47) - на минимум.
2. Матрица
(48)
составленная из коэффициентов при неизвестных в системе ограничений (43) исходной задачи (42) - (44), и аналогичная матрица
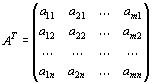(49)
в двойственной задаче (45) - (47) получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов - строками).
3. Число переменных в двойственной задаче (45) - (47) равно числу ограничений в системе (43) исходной задачи (42) - (44), а число ограничений в системе (46) двойственной задачи - числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (45) двойственной задачи (45) - (47) являются свободные члены в системе (43) исходной задачи (42) - (44), а правыми частями в соотношениях системы (46) двойственной задачи - коэффициенты при неизвестных в целевой функции (42) исходной задачи.
5. Если переменная xj исходной задачи (42) - (44) может принимать только лишь положительные значения, то j -е условие в системе (46) двойственной задачи (45) - (47) является неравенством вида “". Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1 - соотношение в системе представляет собой уравнение. Аналогичные связи имеют место между ограничениями (43) исходной задачи (42) - (44) и переменными двойственной задачи (45) - (47). Если i - соотношение в системе (43) исходной задачи является неравенством, то i -я переменная двойственной задачи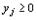 
. В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
|
|
|
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (43) прямой задачи и соотношения (46) двойственной задачи являются неравенствами вида “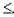 
". Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Теорема двойственности.
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1.
Если Х - некоторый план исходной задачи, a Y - произвольный план двойственной задачи, то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т.е.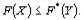 
Лемма 2.
Если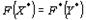 
для некоторых планов X* и Y* задач, то X* - оптимальный план исходной задачи, а Y* - оптимальный план двойственной задачи.
Теорема 8
( первая теорема двойственности). Если одна из задач двойственной пары или, имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т.е.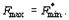 
Если же целевая функция одной задачи из двойственной пары неограничена (для исходной - сверху, для двойственной - снизу), то другая задача вообще не имеет планов.
Теорема 9
( вторая теорема двойственности).
План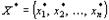 
задачи и план 
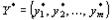задачи, являются оптимальными планами этих задач тогда и только тогда, когда для любого 
выполняется равенство
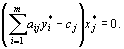
Геометрическая интерпретация двойственных задач. Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трех взаимно исключающих друг друга случаев:
|
|
|
1) обе задачи имеют планы;
2) планы имеет только одна задача;
3) для каждой задачи двойственной пары множество планов пусто.
а) Составить задачу двойственную к примеру 2.
б) Найти её решение любым методом.
в) Найти решение задачи 2, используя теорему двойственности.
а) Задача имеет вид:
| 1 | 1 | ||
| 1 | 2 | ||
| 1 | 3 | ||
| 2 | 1 |
f = 9X1 + 14X2 + 15 X3 + 10X4 → max
| 1 | 1 | 1 | 2 | ||
| 1 | 2 | 3 | 1 |
X1 + X2 + X3 + 2X4 ≤ 3
X1 + 2X2 + 3X3 + X4 ≤ 7
X1, X2, X3, X4 ≥ 0
Составим двойственную задачу по следующей схеме:
число переменных в дв. задаче равно числу ограничений в исходной, а число ограничений в дв. равно числу переменных в исходной;
в дв. задаче меняется вид экстремума (min→max);
векторы правой части и коэффициентов целевой функции в дв. задаче меняются местами: первый становится вектором коэффициентов целевой функции, а второй - вектором правой части в системе ограничений;
левая часть системы ограничений строится по транспонированной матрице (строки меняются со столбцами), которая умножается на вектор переменных двойственной задачи
знаки в системе ограничений двойственной задачи определяются знаками ограничений неотрицательности в исходной задаче.
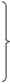g = 3Y1+7Y2 → min
Y1 + Y2 ≥ 9
Y1 + 2Y2 ≥ 14
Y1 + 3Y2 ≥ 15
2Y1 + Y2 ≥ 10
Y1, Y2 ≥ 0
б) Решим задачу графическим методом
в) Оптимальным планом задачи 2, решенной симплексным методом является:
Х2 = (0,2,1,0,0,0); F2 = 9*0+14*2+15*1+0 = 43
Используя 3 симплексную таблицу найдем оптимальный план двойственной задачи.
Из 1 теоремы двойственности следует что: Y=Cб*А - 1
Составим матрицу А из компонентов векторов входящих в оптимальный базис
| 1 | 1 | ||
| 2 | 3 |
А = Р2; Р3 =
Определим обратную матрицу А-1:
| 2 | -1 | ||
| -1 | 1 |
А-1 =Р5; Р6= = (12;
1)
Оптимальный план двойственности равен:
Y = (12, 1, 0, 0, 0, 0); G = 3*12+7*1 = 43
Подставим оптимальный план прямой задачи в систему ограничений
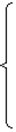
12+1 > 9
12+2*1 = 14
12+3*1 = 15
2*12+1 > 10
Первое ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственная оценка сырья, используемого на производство одного изделия 1 и 4 вида,выше цены этого изделия и, следовательно, выпускать изделия этих видов невыгодно. Его производство и не предусмотрено оптимальным планом прямой задачи. Второе и третье ограничения двойственной задачи выполняются как строгие равенства. Это означает, что двойственные оценки сырья, используемого для производства единицы соответственно изделий 2 и 3 вида, равны в точности их ценам. Поэтому выпускать эти два вида продукции по двойственным оценкам экономически целесообразно. Их производство и предусмотрено оптимальным планом прямой задачи.
|
|
|
Таким образом, двойственные оценки тесным образом связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план, так и на систему оптимальных двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости. К рассмотрению этого мы сейчас и перейдем.
Таким образом, получим тот же результат, который приведен в симплекс-таблице для оптимального решения прямой задачи.
Анализ сопоставления результатов, полученных при решении прямой и двойственной задачи, позволяет сформулировать интересный вывод.
На итерации, приводящей к оптимуму, 
Это равенство справедливо всегда и фактически соответствует оптимальным значениям переменных обеих задач.
Основная и двойственная к ней задачи образуют пару взаимно двойственных задач: двойственная задача к двойственной оказывается основной задачей. Т.е. если мы возьмем двойственную задачу и по теоремам двойственности перейдем ко второй двойственной задаче она окажется прямой задачей.
используя вторую теорему двойственности, найти решение исходной.
Значение линейной функции двойственной задачи от Y численно равно минимальному значению линейной функции исходной задачи
Пропустим процесс решения двойственной ЗЛП, записав только результаты:
Y1=12 Y2=1 Y3=0 min (φ) =43
Т.к max (f) =min (φ), решение исходной задачи уже известно. Остаётся только найти значения X1, X2, X3, при которых это значение достигается. Здесь мы применим вторую теорему двойственности, которая устанавливает следующее соответствие:
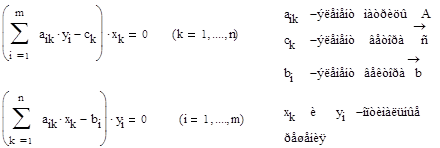
В нашем примере получается следующая система линейных уравнений:
Y1 + Y2 = 9
Y1 + 2Y2 = 14
Y1 + 3Y2 = 15
2Y1 + Y2 = 10
С= (3,7) y1=12 y2=1 т.к. у1>0 и y2>0, то
X1 + X2 + X3 + 2X4 =3
X1 + 2X2 + 3X3 + X4 =7
12+1≠ 9, х1=0
12+2*1=14 → х2≠ 0
12+3*1=15→ х3≠ 0
2*12+1≠10, х4=0
х2+х3=3 Х2*=2
2х2+3х3=7 Х3*=1
F = 9*0+14*2+15*1+0 = 43
|
|
|
12 |
