 |
Определение сложных сигналов
|
|
|
|
Введение
радиолокационный сигнал связь широкополосный
Изобретение радиолокации было обусловлено потребностями военной техники, нуждавшейся в средствах противовоздушной обороны. В ходе второй мировой войны и сразу после ее окончания разработка радиолокационных систем (РЛС) проводилась главным образом с ориентацией на военные применения. Военные системы все еще остаются главной сферой внедрения радиолокационной техники, хотя РЛС используются и для решения самых различных задач - от измерения скорости полета бейсбольного мяча, до картографирования поверхности Венеры. Нижняя граница рабочего диапазона РЛС составляет несколько мегагерц, а верхняя достигает оптической области. Антенны могут быть меньше почтовой марки или в несколько раз больше футбольного поля. Мощности передатчиков РЛС могут быть в пределах от нескольких милливатт до мегаватт. Радиолокационные системы устанавливаются на космических аппаратах, самолетах, судах, танках и в стационарных позициях.
Но реальные показатели РЛС не достигают пока потенциальных теоретических пределов из-за ряда причин. Для их устранения используются различные методы, среди которых использование сложных сигналов.
Целью данной курсовой работы является совершенствование учебно-методического комплекса дисциплины Радиотехнические системы.
Для достижения этой цели необходимо решить следующие задачи:
- Произвести анализ основных видов сложных сигналов;
- Произвести анализ широкополосных систем связи;
- Произвести классификацию радиолокационных систем, их тактических и технических характеристик;
- Обоснование основных путей развития радиолокационных систем со сложными сигналами.
|
|
|
Сложные сигналы
Определение сложных сигналов
Под сложными обычно понимают такие сигналы, для которых произведение их длительности на занимаемую полосу частот значительно больше единицы [2]. Поскольку из соотношения неопределенности следует, что финитные по длительности сигналы не могут иметь финитного спектра, то определение длительности и занимаемой полосы частот нуждается в уточнении. В среднеквадратическом смысле длительность сигнала S(t) и занимаемая им полоса частот выражаются следующим образом:
∆t =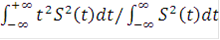 
, (1)
∆ 
= 
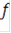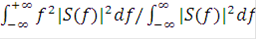, (2)
где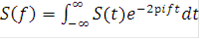 
.
Более реально длительность и полоса определяются долями энергии сигнала 
и 
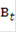на заданном временном интервале ∆t и в заданной полосе частот ∆ .
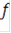Такими сигналами, обеспечивающими наибольшую концентрацию энергии на заданном временном интервале и в заданной полосе частот, оказываются сжатые сфероидальные волновые функции, которые являются собственными функциями интегрального уравнения с ядром вида sint/t. Едва ли можно такие сигналы признать более простыми, чем, например, отрезки гармонических сигналов, даже с точки зрения их формы, не говоря уже о способе формирования. Увеличение длительности сигнала, если оно не сопровождается сужением занимаемой полосы частот, приводит к появлению «сложного» сигнала. Примерами могут служить периодические прямоугольные импульсы, функции Уолша высокого порядка или, наконец, отрезок, состоящий из элементарных ФМ или ЧМ двоичных сигналов, длина которых увеличивается. Классический сложный сигнал - JIЧM (с линейной частотной модуляцией радиоимпульса) является весьма простым с точки зрения его описания и генерирования.
Двоичное избыточное кодирование и прием в целом сигналов, соответствующих кодовым комбинациям, несомненно является случаем использования сложных сигналов (особенно для мощных кодов), однако, по данному выше определению, их сложность имеет тот же порядок, что и при отсутствии всякого кодирования. Действительно, полоса частот при использовании кодов увеличивается в 1/R раз, где R - скорость используемого кода, а в соответствии с теоремой Шеннона можно получить сколь угодно малую вероятность ошибки (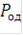
), если R<C, где С - пропускная способность канала связи с помехами. Так, при вероятности ошибки двоичного символа в канале р= 
можно получить 
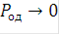, если R≈0,92, т.е. практически без существенного расширения занимаемой полосы частот.
|
|
|
Приведенные выше примеры говорят о том, что определение «сложного» сигнала является нечетким не столько из-за невозможности установления количественной грани между простым и сложным сигналом, сколько из-за многозначности самого понятия «сложности» и «простоты» сигнала. Эти понятия в последнее десятилетие значительно переосмысливались в связи с появлением цифровых методов формирования и обработки сигналов, применением вычислительной техники, новых электронных приборов.
Помимо термина «сложный» сигнал часто используется понятие широкополосного сигнала (в зарубежной литературе их называют сигналами с «растянутым спектром» (spread spectrum)). Обычно широкополосному сигналу дают такое же определение, как и сложному. Тогда к широкополосным относятся сигналы, соответствующие кодовым комбинациям, хотя применение корректирующих кодов почти не требует расширения полосы частот по сравнению с примитивным кодированием.
Иногда определяют систему связи с широкополосными сигналами как систему, в которой передаваемый сигнал занимает полосу частот значительно большую, чем полоса частот передаваемой информации с заданной скоростью. При таком определении корректирующие коды не будут относиться к широкополосным системам, но они, безусловно, остаются сложными сигналами.
Часто используются термины псевдослучайные или псевдошумовые сигналы, которые являются частными случаями широкополосных сигналов.
Положительные свойства сложных сигналов, как правило, связаны с улучшением возможностей приема сигналов или оценивания их параметров в различных каналах связи. Таким образом, сложные сигналы появляются, прежде всего, как следствие оптимизации их структуры. Характерно то, что отношение сигнал-шум на выходе фильтров, согласованных с такими сигналами, оказывается значительно больше, чем на выходе полосового фильтра с оптимальной полосой пропускания (шум в этом случае считается белым).
|
|
|
Сложные сигналы используются в радиолокации, радионавигации и связи в следующих случаях:
. Улучшение точности оценок временных задержек сигналов и сдвигов несущей частоты в каналах связи при наличии помех, в том числе и белого шума.
2. Повышение помехоустойчивости системы передачи дискретных сигналов:
при наличии помех, отличных от белого шума;
при наличии в канале связи выраженной дискретной многолучевости;
в условиях организованных помех с оптимизируемой структурой;
при работе в общей полосе частот многих пар корреспондентов, т.е. при наличии структурных помех.
. Повышение секретности систем радиолокации, радионавигации и связи, т.е. ухудшения возможности их обнаружения и идентификации посторонними лицами.
4. Приближение к реализации пропускных способностей каналов связи, т.е. выбор ансамблей сигналов, обеспечивающих весьма высокую достоверность при высокой информационной скорости передачи.
5. Одновременное обеспечение передачи информации и оценка параметров сигналов.
Весьма важным частным случаем сложных сигналов являются так называемые двоичные составные сигналы, формальное представление которых имеет следующий вид [10]:
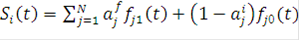, 0 ≤ t ≤ T, (3)
где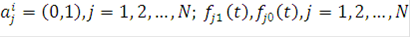 
, - система из 2N ортогональных или биортогональных функций;- «длина» (база) составных сигналов;
Т - длительность составных сигналов.
Полное число составных сигналов вида (1.3) очевидно равно 2N, однако не обязательно все из них могут быть выбраны в системе связи. В частном случае для передачи одного информационного бита можно использовать всего два вида сигналов -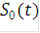 
и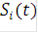 
.
Функции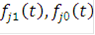 
могут быть выбраны, вообще говоря, перекрывающимися как в частотной, так и во временной области, но обычно ортогональность обеспечивается тем, что эти функции не перекрываются во времени или (и) частоте. В частности, обеспечение ортогональности за счет временных сдвигов приводит к следующей структуре двоичных составных сигналов:
|
|
|
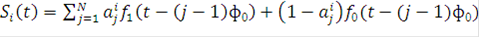, (4)
где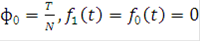 
при t < 0 и t > 
.
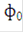Фактически запись (4) означает, что сигналы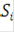 
(t) представляют собой последовательность сигналов 
и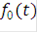 
длительностью 
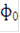, закон чередования которых определяется двоичными наборами (
).
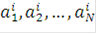Наиболее важным частным случаем (4) является использование в качестве элементарных сигналов («чипов») отрезков гармонического сигнала с модуляцией фазы на р. Такие сигналы называют двоичными составными ФМ сигналами. Ясно, что «сложность» сигналов в последнем случае и как следствие их положительные свойства определяются только двоичными наборами ().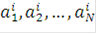
Заменяя временной сдвиг в (4) сдвигом по частоте, легко получить частотно-составные сигналы, а осуществляя одновременно различные сдвиги по времени и частоте, еще более сложные структуры - частотно-временные матрицы (ЧВМ). Достаточно подробная классификация ЧВМ и их основные свойства даны в [1] и здесь не будем на них останавливаться.
Одно из простых обобщений представления (4) состоит в том, что используется не 2, a q различных элементарных функций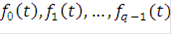 
и, следовательно, не двоичный, а q-ичный набор 
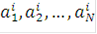. Частный случай такого представления - гармонические многофазные элементарные сигналы.
Более существенно такое обобщение (4) (каскадные сигналы), когда элементарные сигналы сами являются двоичными составными сигналами, т.е.
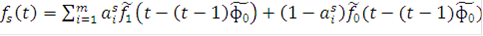, (5)
где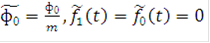 
при t < 0, t > 
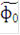; S = 0, 1,..., q-1.
Очевидно дальнейшее обобщение (5), когда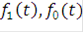 
также составные сигналы и т.д.
Данная конструкция, по существу, представляет собой непрерывный аналог каскадных кодов.
Обратимся теперь к возможным способам обработки составных сигналов. Известно, что для функций, принадлежащих пространству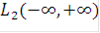 
(интегрируемых с квадратом на интервале (
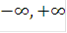)), к которым всегда можно отнести физически реальные сигналы u(t), любое линейное преобразование Lu может быть представлено в следующем виде:
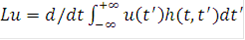, (6)
где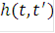 
- функция из 
.
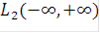Частным случаем (6) является преобразование свертки
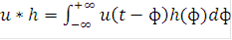, (7)
где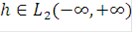 
,
а частным случаем (7) - корреляционная обработка сигнала
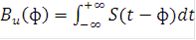, (8)
где S(t) - передаваемый сигнал.
Линейное преобразование принимаемых сигналов - это часть оптимальной (с точки зрения минимума вероятности ошибки) обработки принимаемых сигналов для постоянного канала с коррелированным гауссовским шумом, для канала с гауссовским шумом и неопределенной фазой и для некоторых моделей каналов со случайными параметрами. Корреляционная обработка (8) оптимальна для канала с гауссовским белым шумом. В каналах с негауссовскими аддитивными помехами оптимальная обработка входных сигналов часто оказывается нелинейной, однако и в этом случае она требует на определенном этапе корреляционной обработки преобразованных сигналов [10].
|
|
|
Таким образом, преобразование свертки (7) и корреляционный интеграл (8) являются весьма важными процедурами при обработке сигналов в задачах радиолокации, навигации и связи. При использовании в этих системах сложных сигналов, в частности составных сигналов с большой базой, реализация свертки связана со значительными трудностями даже при цифровой обработке и при наличии микропроцессорной техники. Задачи обработки сигналов существенно усложняются из-за необходимости обеспечения синхронизации сложных сигналов.
Виды сложных сигналов
Сигнал с линейной частотной модуляцией (ЛЧМ) представляет собой радиоимпульс, частота которого линейно изменяется (увеличивается или уменьшается) от начала к концу импульса. Фильтр, оптимальный для ЛЧМ-радиоимпульса должен иметь импульсную характеристику в виде ЛЧМ-импульса, зеркально отображенного относительно сигнала. Если у исходного радиоимпульса сгущения были справа, а разрежения - слева (левый график на рисунке 1), то у импульсной характеристики расположение сгущений и разрежения должно быть противоположным (правый график рисунке 1). Реализуется фильтр на основе линии задержки с неравностоящими отводами, полосового фильтра и интегратора. Отводы должны быть расположены в соответствии с требуемой импульсной характеристикой. На рисунке 2 приведены эпюры напряжений оптимального фильтра для сигнала без внутриимпульсной модуляции (слева) и сигналов с ЛЧМ (справа).
Рисунок 1- Вид ЛЧМ сигналов
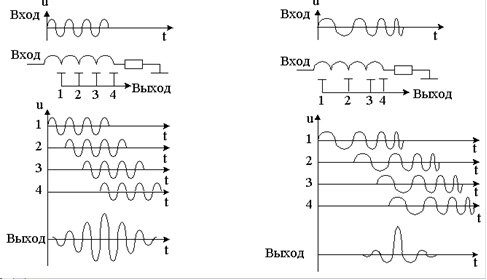
Рисунок 2- Принцип работы фильтров для тонального и ЛЧМ сигналов
Для простого радиоимпульса без внутриимпульсной модуляции отводы линии задержки должны быть расположены равномерно. С каждого отвода снимается частотно-модулированный импульc. Сигналы с отводов линии задержки суммируются. Расположение отводов подобрано так, чтобы в момент окончания импульсов на выходе линии задержки происходило суммирование всех положительных полупериодов. Амплитуда результирующего колебания в другие моменты времени близка к нулю. Длительность выходного импульса существенно меньше длительности входного.
Корреляционная функция или отклик СФ имеет вид, приведённый на рисунке 3:
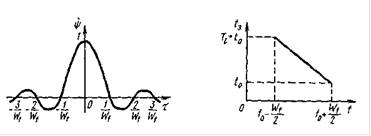
Рисунок 3 - Корреляционная функция или отклик СФ
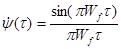. (9)
Фазоманипулированный сигнал. Кроме плавного изменения частоты сигнала, как это бывает в случае ЛЧМ, также возможно изменение фазы сигнала. Технически проще реализуется дискретное изменение фазы. Такой сигнал называется фазоманипулированным. Наибольшее распространение получила фазовая манипуляция по равномерным кодам (Хэмминга, Баркера и др.). Таким образом, радиоимпульс с фазовой манипуляцией представляет собой дискретный сигнал, обычно с прямоугольной огибающей, фаза которого в дискретные моменты времени скачком меняет свое значение по определенному коду. Пример такого сигнала приведен на рисунке 4 а, а закон манипуляции - на рисунке 4 б. В верхней части рисунка 4 приведена структурная схема фильтра, согласованного с указанным сигналом. Фильтр построен на основе линии задержки с отводами. В цепи отводов помещены усилители с единичным коэффициентом усиления, но с инверсией или без нее. Знаки коэффициентов усиления (импульсная характеристика фильтра) устанавливаются зеркальными относительно сигнала. Таким образом, К1 =1, К2= -1, К3=1, К4=1. Здесь единица означает усиление без инверсии, минус единица - усиление с инверсией. Для четырехэлементного кода импульс укорачивается в 4 раза. Использование такого фильтра позволяет работать при мощности шума, превышающей мощность сигнала на входе в 2-3 раза. На выходе такого звена обычно ставят фильтр, согласованный с одиночным элементарным радиоимпульсом [8].
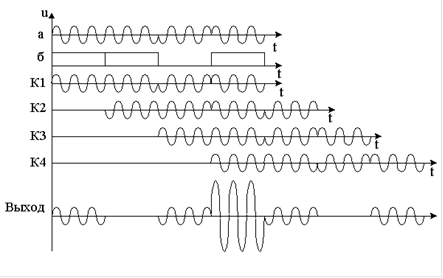
Рисунок 4- Принцип работы СФ фазоманипулированного сигнала
|
|
|
