 |
Параллельное проектирование
|
|
|
|
АФФИННЫЕ ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ
Аффинное отображение - такое отображение плоскости (пространства) на другую плоскость (пространство), при котором каждая прямая отображается в прямую (рис.1). Аффинное преобразование есть аффинное отображение плоскости на себя.
|

|
Математический аппарат аффинных преобразований лежит в основе построения изображений в компьютерной графике.

|
Преобразование, которое переводит точку М (x,y) в другую точку М*(x*,y*), (рис.2), задается формулами
x* = a x + b y + l (11)
y* = g x + d y + m
где a, b, l, g, d, m - произвольные числа, связанные неравенством:

 a b
a b
¹ 0
G d
В аффинных преобразованиях на плоскости особую роль играют несколько важных частных случаев, имеющих четкую геометрическую интерпретацию, а именно:
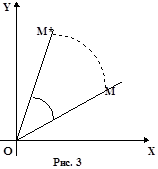
|
а). Поворот вокруг начальной точки на угол j (рис. 3).
x* = x cos j - y sin j (21)
y* = x sin j + y cos j
|
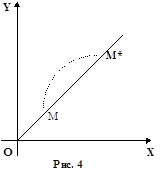
б). Растяжение (сжатие) вдоль координатных осей (рис. 4).
x* = a x (31)
y* = d y
Для растяжения: a > 1; d > 1; для сжатия: 1 > a > 0; 1 > d > 0.
в). Отражение относительно оси абсцисс (рис. 5).
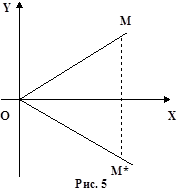
|
x* = x (41)
y* = - y
г). Перенос (рис. 6).
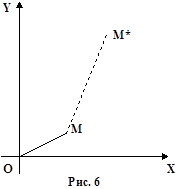
|
x* = x + l (51)
y* = y + m
где l, m - координаты вектора переноса М М*.
ОДНОРОДНЫЕ КООРДИНАТЫ ТОЧКИ
Однородными координатами точки М(x,y) называется любая тройка одновременно не равных нулю чисел x 1, x 2, x 3, связанных с заданными координатами (x,y) следующими соотношениями:
x 1 /x 3 = x; x 2 /x 3 =y; (61)
То есть, в общем случае однородные координаты точки можно представить тройкой (hx, hy, h). При решении задач компьютерной графики обычно используется частный случай, а именно: произвольной точке М (x,y) на плоскости ставится в соответствие точка М*(x,y,1) в пространстве (рис. 7).
|
|
|

|
При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.
АФФИННЫЕ ПРЕОБРАЗОВАНИЯ В ПРОСТРАНСТВЕ
Аналогично тому, как это было сделано для двумерного случая, заменим координатную тройку (x, у, z), задающую точку в пространстве, на четверку (x, у, z, 1) или в общем виде на (hx, hy, hz, 1), где h ¹ 0.
Можно показать, что любое аффинное преобразование в трехмерном пространстве может быть представлено в виде комбинации поворотов, растяжений (сжатий), отражений и переносов. Выпишем все матрицы, определяющие эти преобразования:
А. Матрицы поворота в пространстве
Матрица поворота вокруг оси абцисс на угол j:
 |  |
1 0 0 0
R x = 0 cos j sin j 0 (1)
0 - sin j cos j 0
0 0 0 1
Матрица поворота вокруг оси ординат на угол y:
 |  | ||
cos y 0 - sin y 0
R y = 0 1 0 0 (2)
sin y 0 cos y 0
0 0 0 1
Матрица поворота вокруг оси аппликат на угол c:
 |  |
cos c sin c 0 0
R z = - sin c cos c 0 0 (3)
0 0 1 0
0 0 0 1
Б. Матрица растяжения (сжатия)
 |  |
a 0 0 0
D = 0 b 0 0 (4)
0 0 g 0
0 0 0 1
где a, b, g - коэффициенты растяжения (сжатия) вдоль осей абсцисс, ординат и аппликат, соответственно.
В. Матрицы отражения:
Матрица отражения относительно плоскости XY:
 |  |
1 0 0 0
М z = 0 1 0 0 (5)
0 0 - 10
0 0 0 1
Матрица отражения относительно плоскости YZ:
 | |||
 | |||
- 1 0 0 0
М x = 0 1 0 0 (6)
0 0 10
0 0 0 1
Матрица отражения относительно плоскости ZX:
 |  |
1 0 0 0
М y = 0 - 1 0 0 (7)
0 0 10
0 0 0 1
Г. Матрица переноса
 |  |
1 0 0 0
T = 0 1 0 0 (8)
0 0 10
l m n 1
где (l, m, n) - вектор переноса.
Матрицы (1 ¸ 8) отражают простейшие геометрические преобразования точки в пространстве. Матрица сложного аффинного преобразования получается в результате перемножения такого рода матриц и имеет в общем случае вид:
|
|
|
 |  |
a1 a2 a3 0
P = b1 b2 b3 0 (9)
g1 g2 g3 0
l m n 1
При помощи указанных матриц можно преобразовывать любые пространственные тела, заданные множеством вершин, соединенных отрезками прямых.
Пусть требуется подвергнуть заданному аффинному преобразованию выпуклый многогранник, имеющий n вершин (рис. 1). Матрица, однозначно описывающая такое тело, имеет вид:
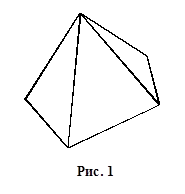
|
 |  |
x 1 y 1 z 1 1
x 2 y 2 z 2 1
V 0 =.... (10)
....
x n y n z n 1
где x i, y i, z i - координаты i - й вершины.
По геометрическому описанию преобразования находим его матрицу P. Тогда новый выпуклый многогранник описывается набором вершин:

 x 1 * y 1 * z 1 * 1
x 1 * y 1 * z 1 * 1
x 2 *y 2 *z 2 * 1
V* = V 0 * P =.... (11)
....
x n *y n * z n * 1
ВИДЫ ПРОЕКТИРОВАНИЯ
Так как экран дисплея представляет собой двумерное пространство, мы можем изобразить только проекции трехмерных объектов, а не сами объекты. Задача состоит в том, чтобы определить проекцию каждой точки объекта, расположенного в произвольном месте трехмерного пространства, на некоторую плоскость в этом пространстве, называемую картинной плоскостью.
Изображение объектов на картинной плоскости связано с еще одной геометрической операцией - проектированием с помощью пучка прямых. В компьютерной графике используется несколько видов проектирования. Наиболее часто встречается проектирование центральное (перспективное) и параллельное.
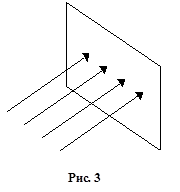
|
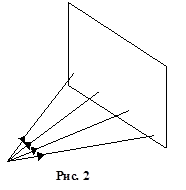
|
Для получения проекции объекта на картинную плоскость необходимо провести через каждую его точку прямую из заданного проектирующего пучка и затем найти координаты точки пересечения этой прямой с плоскостью изображения. В случае центрального проектирования все прямые исходят из одной точки - центра пучка (рис. 2). При параллельном проектировании центр пучка считается лежащим в бесконечности (рис. 3).
Каждый из этих двух основных классов разбивается на несколько подклассов в зависимости от взаимного расположения картинной плоскости и координатных осей. Классификация параллельных и центральных (перспективных) проекций приводится на рис.4 и рис.5, соответственно.
|
|
|
ПАРАЛЛЕЛЬНОЕ ПРОЕКТИРОВАНИЕ
Как видно из рис.4, среди параллельных проекций различают ортографическую, аксонометрическую и косоугольную.
При ортографической проекции картинная плоскость совпадает с одной из координатных плоскостей (рис.6) или параллельна ей (рис.7). Проектирующие прямые перпендикулярны картинной плоскости.

|
|
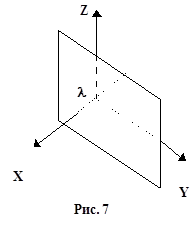
|
|
Так как проектирование можно рассматривать как вид геометрических преобразований, для его описания в задачах компьютерной графики используются однородные координаты и матрицы четвертого порядка. В частности, для ортографической проекции матрица проектирования вдоль оси X на плоскость YZ имеет вид:
 |  |
0 0 0 0
P x = 0 1 0 0 (12)
0 0 1 0
0 0 0 1
Если картинная плоскость параллельна координатной плоскости и перенос составляет величину l (рис.7), необходимо умножить матрицу P x на матрицу переноса (8), учитывая при этом, что m = 0 и n = 0.
 |  |  |  |
1 0 0 0 0 0 0 0
P xl = P x * 0 1 0 0 = 0 1 0 0 (13)
0 0 1 0 0 0 1 0
l 0 0 1 l 0 0 1
Аналогично для матриц проектирования вдоль двух других координатных осей:
 |  |
1 0 0 0
P ym = 0 0 0 0 (14)
0 0 1 0
0 m 0 1
 |  |
1 0 0 0
P zn = 0 1 0 0 (15)
0 0 0 0
0 0 n 1
При аксонометрической проекции проектирующие прямые перпендикулярны картинной плоскости, а сама картинная плоскость образует с осями координат ненулевые углы. Если все три угла различны между собой - проекция триметрическая; если два угла из трех равны - проекция диметрическая; если равны все три угла - проекция изометрическая. Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование.
Так, например, при повороте на угол y относительно оси ординат (2), на угол j вокруг оси абсцисс (1) и при последующем проектировании вдоль оси аппликат (15) необходимо построить матрицу:
 |  |  |  |  |
 cos y 0 - sin y 0 1 0 0 0 1 0 0 0
cos y 0 - sin y 0 1 0 0 0 1 0 0 0
М = 0 1 0 0 * 0 cos j sin j 0 * 0 1 0 0 (16)
sin y 0 cos y 0 0 - sin j cos j 0 0 0 0 0
|
|
|
0 0 0 1 0 0 0 1 0 0 n 1
Проекции, для получения которых используется пучок прямых, не перпендикулярных картинной плоскости, называют косоугольными. Среди них различают свободную проекцию, когда угол наклона проектирующих прямых к картинной плоскости равен половине прямого, и кабинетную проекцию, когда требуется еще, чтобы масштаб по одной из осей был вдвое меньше, чем по двум остальным осям.
|
|
|


