Примеры атрибутных грамматик

Ниже рассматриваются некоторые примеры применения атрибутных грамматик для решения различных задач.

Пример 1. Грамматика, разработанная Д. Кнутом [2] для представления рациональных чисел. Эта грамматика задается следующими порождающими правилами (продукциями):

S::= L.L;

L::= LB/B; (П1)

B::= 0/1

С помощью этой грамматики порождаются последовательности вида 01011.101; 1.001101 и т. п. Например, последовательность 110.01 может быть выведена с помощью следующих подстановок: S → L.L → LB.L → L0.LB → LB0.L1 → B10.B1→110.01. Дерево вывода для этой последовательности показано на рис. 1.

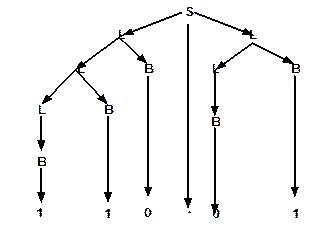Рис. 1 Дерево вывода последовательности 110.01

 

Пусть значение, приписываемое каждой двоичной последовательности – это численное значение соответствующего двоичного числа. Так, по последовательности 110.01 компилятор должен вычислить величину 6.25 (в машинном представлении). Для этого каждому нетерминальному символу следует приписать семантические атрибуты, как это показано в табл.1:

Таблица 1. Соответствие атрибутов нетерминальным символам.

Нетерм.симв	Атр	Примечание
В	B.υ	υ – целочисл. знач-ие, припис-ое двоичн. симв., представл. В.
L	L.υ	υ – целочисл. знач-ие, припис-ое послед-сти двоичн. симв-в, выведенных из L.
L	L.l	l – длина послед-сти двоичных символов, выведенных из L.
S	S.υ	υ – численное значение, приписываемое двоичной последовательности символов, выведенных из S.

 

Таблица 2. Атрибутная грамматика двоичных чисел.

№	Продукции	Семантические правила
	S::= L.L	S.υ:= L1.υ+ L2.υ/2 L2l
	L::= LB	L.υ:=
	L::= B	L.υ:= B.υ
	B::= 0	B.υ:=0
	B::= 1	B.υ:=1

__________________________________

В таблице 2 различные нетерминальные символы снабжены индексами, чтобы было удобнее различать их параметры в соответствующем семантическом правиле. Ясно, что в рассматриваемом примере значения атрибутов всех нетерминальных символов, стоящих в левых частях продукций, определяются через значения атрибутов их непосредственных потомков в правых частях, откуда следует синтезированность всех атрибутов. Структуру дерева вывода любой последовательности, принадлежащей данной грамматике, можно расширить, добавив атрибуты и их значения во всех узлах. Тем самым будет построено аннотированное дерево, показанное на рис. 2:

 

 

Рис. 2 показывает, что значением последовательности 110.01 является 6.25 в десятичном представлении. Вычисления значений этих синтезированных атрибутов происходит по дереву снизу вверх в соответствии с правилами, определенными в атрибутной грамматике, представленной в таблице 3.

Пример 2. Пусть для управления положением режущего инструмента некоторого станка с ЧПУ используется специализированный язык, предложения которого представляют собой перечисления отдельных шагов перемещения резца по заданной траектории. Каждый шаг имеет длину в одну условную единицу (миллиметр, микрон и т. п.) и одно из четырех направлений движения: «вверх», «вниз», «вправо», «влево». Таким образом, перемещение резца происходит на координатной плоскости. Синтаксические правила для такой грамматики могут иметь, например, такой вид:

 

S::= start <Коорд> stop

<Коорд>::= <Коорд><Delta>/<Delta>

<Delta>::= «вверх»/ «вниз»/ «вправо»/ «влево»

Определенная таким образом грамматика, очевидно, является контекстно – свободной. Нетерминальный символ <Коорд> означает текущее положение резца, нетерминальный символ S, таким образом, есть конечное положение резца. Тогда с этими нетерминальными символами можно связать двухкомпонентный вектор v = (x,y), имеющий смысл пары координат, приписанных одному из этих нетерминальных символов. Если этот же вектор связать с нетерминальным символом <Delta>, то его можно интерпретировать как приращение текущей координаты. Исходя из этих соображений, можно следующим образом определить атрибутную грамматику (табл. 3).

Таблица 3. Атрибутная грамматика языка для управления режущего инструмента.

№	Продукции	Семантические правила
	S::=start<Коорд> stop	S.v:= <Коорд>.v
	<Коорд>1::=<Коорд>2<Delta>	<Коорд>1.v = <Коорд>2.v+<Delta>.v
	<Коорд>::=<Delta>	<Коорд>.v=<Delta>.v
	<Delta>::= «вверх»	<Delta>.v=(0,1)
	<Delta>::= «вниз»	<Delta>.v=(0,-1)
	<Delta>::= «вправо»	<Delta>.v=(-1,0)
	<Delta>::= «влево»	<Delta>.v=(1,0)

 

 

start «вверх» «вверх» «вниз»«влево» «вверх» «вправо» «вверх» stop показано на рис. 9.

 

 

Рис. 9. Аннотированное дерево вывода вычисления координат.

 

Поделиться:

Воспользуйтесь поиском по сайту: