Параллельное соединение коротких трубопроводов

Закон Архимеда

 

Применим рассмотренный выше прием определения вертикальной силы давления жидкости на криволинейную стенку для доказательства закона Архимеда. Пусть в жидкость помещено тело произвольной формы (рис. 1.11) объемом V.

Спроектируем это тело на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Вертикальная составляющая силы полного давления жидкости P_z1, действующая на верхнюю часть тела,

,

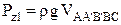(1.61)

а на нижнюю часть –

.

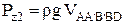(1.62)

Все горизонтальные силы, действующие на тело, уравновешены. Совершенно очевидно, что P_z2 > P_z1, следовательно возникает выталкивающая сила

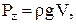
(1.63)

где V – объем тела.

Таким образом, на тело, погруженное в жидкость, действует сила, равная весу жидкости в объеме тела.

В зависимости от соотношения веса тела G и силы P_z (архимедовой силы) возможны, как известно, три варианта положения тела: G>P_z – тело тонет; G<P_z – всплывает; G=P_z – находится в безразличном равновесии.

2. Основы кинематики и динамики жидкости

 

2.1. Методы описания движения жидкостей

 

Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости и применение этих законов к решению практических задач.

Существуют разные способы описания движения жидкости, из которых наибольшее распространение имеют методы Лагранжа и Эйлера.

При исследовании по методу Лагранжа изучается движение отдельных частиц жидкости вдоль их траекторий. Для выделения из бесчисленного множества траекторий частиц той, которая принадлежит данной частице, отмечают ее координаты a, b, c в начальный момент времени t_о. Координаты x, y, z и скорости v_x, v_y, v_z зависят от начальных координат:

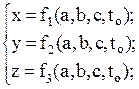
		(2.1)
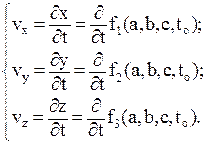
		(2.2)

По методу Эйлера определяют скорость и давление жидкости в той или иной точке пространства:

(2.3)

В гидравлике наибольшее распространение получил метод Эйлера, так как он проще метода Лагранжа.

Существует два вида движения жидкости – неустановившееся, когда скорость и давление зависят от координат и времени, и установившееся, когда указанные параметры не зависят от времени.

В дальнейшем будем рассматривать только установившееся движение жидкости. Установившееся движение, при котором частицы жидкости сохраняют свою скорость одинаковой по длине потока, называется равномерным.

На практике встречаются следующие виды потоков – напорные, безнапорные, струи. В напорных потоках все поперечное сечение трубы, канала заполнено жидкостью, движение которой осуществляется под напором, создаваемым тем или иным источником энергии.

Безнапорные потоки имеют свободную поверхность. Такое движение осуществляется в каналах, руслах рек, трубопроводах, работающих неполным сечением за счет сил тяжести.

Струи – это потоки, имеющие свободную поверхность по всему периметру сечения, движение здесь осуществляется за счет сил инерции.

 

2.2. Понятие о струйчатой модели потока

 

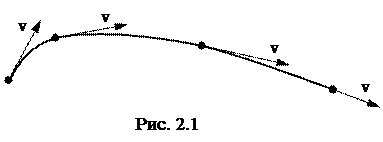В гидравлике для изучения закономерностей движения жидкости широко используется струйчатая модель потока. В соответствии с этой моделью поток состоит из бесконечного множества элементарных струек. Введем понятие об элементарной струйке. Если изобразить скорость каждой частицы жидкости в пространственном потоке в виде вектора, то получим векторное поле скоростей. Проведем в этом поле линию так, чтобы векторы скорости были направлены по касательной к этой линии. Линия, полученная таким образом, называется линией тока (рис. 2.1).

Траекторией называется путь, описанный частицей в пространстве. При установившемся движении линия тока совпадает с траекторией, при неустановившемся не совпадает.

Если в движущейся жидкости взять элементарный замкнутый контур и через каждую точку этого контура провести линию тока, то получим трубку
тока. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. Сечение струйки, нормальное к ее линиям тока, называется живым сечением элементарной струйки (рис. 2.2).

В силу того, что площадь сечения элементарной струйки бесконечно мала, можно считать, что в каждой точке значения скорости одинаковы. Трубка тока непроницаема для жидкости.

Потоком жидкости называется совокупность элементарных струек, текущих в заданных границах.

Живым сечением F называется поверхность, проведенная в границах потока и нормальная ко всем линиям тока.

Смоченным периметром c называется часть периметра живого сечения, соприкасающаяся с ограждающими стенками.

Гидравлический диаметр D_г представляет собой отношение учетверенной площади живого сечения к смоченному периметру:

.

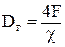(2.4)

Гидравлический радиус R_г – это отношение площади живого сечения к смоченному периметру:

.

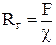(2.5)

Количество жидкости, проходящей через живое сечение в единицу времени, называется расходом.

Расход бывает трех видов: объемный (dQ=vdF), весовой (dG=rgvdF) и массовый (dM=rvdF).

Значения скорости различных струек в потоке различны, поэтому расход потока складывается из элементарных расходов струек:

.

(2.6)

Интеграл (2.6) не берется, так как неизвестен закон распределения скоростей по сечению потока.

Введем понятие средней скорости:

.

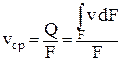(2.7)

Средняя скорость потока равна частному от деления объемного расхода жидкости на площадь живого сечения потока.

Введя понятие о расходе жидкости, легко получить уравнение неразрывности – одно из основных уравнений гидравлики. Будем рассматривать жидкость как сплошную среду, не имеющую при движении разрывов и пустот в потоке. Для элементарной струйки условие неразрывности можно записать следующим образом (см. рис. 2.2):

.

(2.8)

Для потока жидкости

.

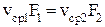(2.9)

Уравнение (2.9) является уравнением неразрывности для потока несжимаемой жидкости. Если речь идет о сжимаемой жидкости, то уравнение неразрывности будет иметь вид:

,

(2.10)

где ρ₁ и ρ₂ – плотность жидкости в сечениях 1 и 2.

 

2.3. Дифференциальные уравнения Эйлера

для движения идеальной жидкости

 

Идеальной жидкостью называется жидкость абсолютно несжимаемая, обладающая абсолютной подвижностью частиц и не имеющая вязкости. Анализ движения такой жидкости позволит выяснить основные закономерности, которые после учета сил трения дадут возможность производить расчеты потока.

Вырежем в жидкости элементарный параллелепипед с ребрами dx, dy, dz

и отбросим окружающую жидкость. Заменим воздействие окружающей жидкости на параллелепипед силами (рис. 2.3).

На грань 1234 действует сила

,

(2.11)

на грань 5678 –

.

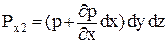(2.12)

Массовая сила G в проекции на ось х запишется так:

,

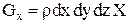(2.13)

где Х – проекция ускорения массовой силы на ось х.

Применим к рассматриваемому элементу теорему количества движения. Изменение количества движения массы жидкости, сосредоточенной внутри объема, происходит вследствие того, что каждая частица, перемещаясь, с течением времени занимает новое положение и приобретает новую скорость, а также потому, что в каждой точке пространства скорость меняется во времени.

Введем импульс массовых сил в проекции на ось х:

.

(2.14)

Тогда суммарный импульс равен изменению количества движения:

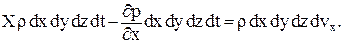
(2.15)

Следовательно,

.

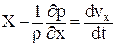(2.16)

Аналогично выводятся зависимости для других осей.

Таким образом, получим дифференциальные уравнения Эйлера для движения идеальной жидкости:

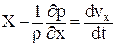	;	(2.17)
	;
	.

Уравнения (2.17) показывают, что ускорение жидкого элемен­та вызывается соответствующими изменениями сил давления, дейст­вующих на этот элемент, и массовыми силами.

Уравнения Эйлера могут быть при известных условиях проинтег­рированы. Пусть имеет место стационарное течение. Умножим левую и правую части каждого уравнения соответственно на dx, dy, dz и произведем почленное сложение:

.

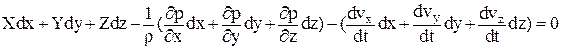(2.18)

Предположим, что в жидкости действуют только силы тяжести.
Тогда Х = 0; Y = 0; Z = – g.

Для установившегося движения, когда p = f(x,y,z),

.

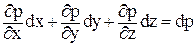(2.19)

Так как , то

.

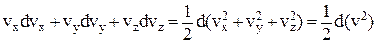(2.20)

Итак, дифференциальное уравнение (2.18) примет вид:

(2.21)

или

.

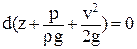(2.22)

После интегрирования уравнения (2.22) получим:

.

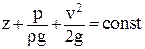(2.23)

Выражение (2.23) представляет собой уравнение (интеграл) Бернулли для установившегося течения струйки несжимаемой жид­кости. В уравнении (2.23) 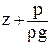– геометрический и пьезометрический напор, – скоростной (динамический) напор.

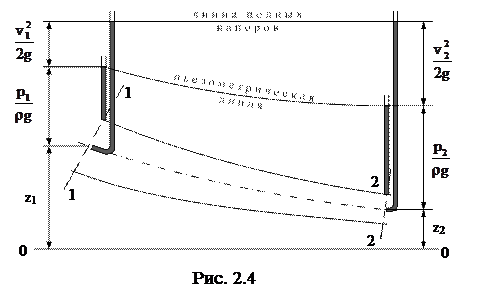
Следовательно, согласно уравнению Бернулли сумма скорост­ного, пьезометрического и геометрического напоров есть величина постоянная для любых

сечений элементарной струйки идеальной жидкости при установившемся
движении (рис. 2.4).

Известно, что 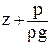представляет собой удельную потенциальную энергию жидкости, а – удельную кинетичес-кую. Исходя из этого уравнение Бернулли устанавливает постоянство суммы удельных кинетической и потенциальной энергии идеальной жидкости в установившемся движении и является частным случаем закона сохранения энергии.

 

2.4. Уравнение Бернулли для потока реальной (вязкой) жидкости

 

Полученное уравнение Бернулли при определенных услови­ях можно распространить на поток реальной жидкости. Рассмотрим так называемое плавно изменяющееся движение жидкости, у которо­го наблюдается параллельно-струйное движение и давление по се­чению потока распределяется по гидростатическому закону (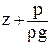 = const).

Как известно, полная удельная энергия элементарной струйки

.

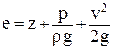(2.24)

Умножим левую и правую части уравнения (2.24) на весовой рас­ход струйки rgvdF, тогда полная энергия, которую переносит элементарная струйка через сечение dF в единицу времени,

.

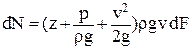(2.25)

Легко убедиться в том, что в левой и правой частях уравнения (2.25) будет размерность мощности. В силу того, что поток состоит из бесконечного множества элементарных струек, мощность потока в любом сечении

.

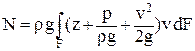(2.26)

Разобьем интеграл в правой части выражения (2.26) на два:

.

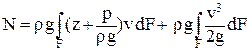(2.27)

Так как давление по сечению изменяется по гидростатическому закону, то

.

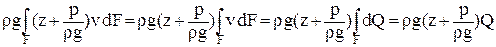(2.28)

Рассмотрим второй интеграл и представим его в виде:

.

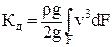(2.29)

Интеграл (2.29) не берется, так как неизвестен закон рас­пределения скорости по сечению потока. Этот интеграл представ­ляет собой действительную кинетическую энергию, переносимую потоком через данное поперечное сечение в единицу времени (обоз­начим ее К_д).

Предположим, что значения скорости в каждой точке поперечного сече­ния потока одинаковы и равны средней скорости: 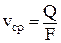. Тогда кинетическая энергия, подсчитанная по средней скорости,

.

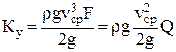(2.30)

Обозначим

,

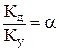(2.31)

тогда

.

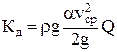(2.32)

Коэффициент a носит название коэффициента неравномер­ности распределения скорости по сечению, или коэффициента ки­нетической энергии; он представляет собой отношение действи­тельной кинетической энергии весового секундного расхода по­тока к его кинетической энергии, вычисленной по средней скорости. Величина коэффициента a определяется опытным путем. Для турбулентного режима a = 1,1, для ламинарного – 2.

Подставляя значения интегралов (2.29) и (2.33) в (2.28), получим:

.

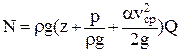(2.33)

Разделим левую и правую части уравнения (2.33) на весовой расход потока rgQ и получим:

,

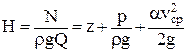(2.34)

где Н – полная удельная энергия жидкости, протекающей через рассматриваемое живое сечение потока в единицу времени, или полный напор в данном сечении.

Полученное выражение (2.34) справедливо для любого сечения потока, и если составить баланс энергий для двух сечений потока, то:

Н1 = Н2 + hw,

(2.35)

где h_w – потеря энергии между сечениями 1 и 2.

Следовательно, подставив в уравнение (2.35) значения 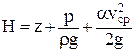, получим:

.

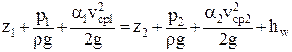(2.36)

Уравнение (2.36) носит название «уравнение Бернулли для потока реальной жидкости» и является основным уравнением гидравли­ки, устанавливающим баланс энергии в потоке жидкости. В дальнейшем индексы «ср» у скорости ставить не будем, помня о том, что скорость в уравнении (2.36) является средней. Заметим, что практически все расчеты потоков производятся с помощью урав­нения Бернулли.

 

2.5. Гидравлические сопротивления, их физическая природа и классификация (общие сведения)

 

Определение потерь энергии в потоке является важнейшим вопросом любого гидравлического расчета. Различают два вида гидравлических сопротивлений: местные и по длине.

Местные сопротивления обусловлены изменениями формы и раз­меров русла, вызывающими деформацию потока. При протекании по местным сопротивлениям возникают интенсивные вихри, которые и вызывают в конечном счете потери энергии. В качестве примеров местных сопротивлений можно назвать вентили, задвижки, внезап­ные расширения и сужения русла, диафрагмы, повороты и т. д.

Местные потери энергии в трубопроводах рассчитываются по формуле

,

(2.37)

где буквой z обозначают коэффициент местного сопротивления;

v – средняя скорость в трубопроводе.

Формулу (2.37) называют формулой Вейсбаха. Каждое местное сопротивление характеризуется своим значением коэффициента z.

Потери по длине – это потери, которые возникают в прямых трубах постоянного сечения. Этот вид потерь обусловлен внутренним трением в жидкости и возникает как в гладких, так и в шероховатых трубах.

Потерю напора по длине рассчитывают по формуле:

,

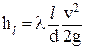(2.38)

где h _l – потеря по длине, м;

l – длина участка трубы, м;

d – диаметр трубы, м;

l – коэффициент сопротивления трения.

Формулу (2.38) называют формулой Дарси.

Общие потери в потоке складываются из суммы потерь, вызван­ных каждым сопротивлением:

(2.39)

Такое представление о сложении потерь называется принципом нало­жения.

 

 

3. Режимы течения жидкостей в трубах и
основы теории подобия

 

3.1. Режимы течения жидкостей в трубах. Опыты Рейнольдса.

Понятие о критическом числе Рейнольдса

Опытами установлено, что существуют два основных режима движения жидкостей – ламинарный и турбулентный.

При ламинарном режиме жидкость движется скользящими друг по другу несмешивающимися струйками или слоями.

При турбулентном режиме отдельные частицы жидкости движутся по произвольным сложным траекториям, происходит интенсивное пе­ремешивание частиц жидкости.

Впервые предположение о существовании двух режимов движения жидкости было высказано Д. И. Менделеевым. Несколько позже английский физик О. Рейнольдс опытным путем подтвердил это пред­положение. Опытная установка для визуального наблюдения Рей­нольдса представляла собой резервуар 1 (рис. 3.1), к которому присоединялся прозрачный трубопровод 2 с запорным устройством 3. Мерный бак 4 позволял измерять расход Q и, следовательно, среднюю скорость 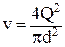в прозрачном трубопроводе. Для того чтобы сделать поток видимым, из малого резервуара 5 по тонкой трубке в основной поток подавалась краска.

Рис. 3.1

 

Наблюдения показали, что при малой скорости движения жид­кости струйка краски движется в трубе параллельно стенкам в ви­де тонкой нити, не смешиваясь с основной массой жидкости. Такой режим движения жидкости называется ламинарным (рис. 3.2, а).

 

При увеличении скорости движения жидкости наблюдается нару­шение устойчивости ламинарного движения (рис. 3.2, б). Струйка краски приобретает волнистую форму, в ней появляются разрывы. Дальнейшее увеличение скорости потока приводит к полному разру­шению струйки краски и окрашиванию всей массы жидкости в один цвет. Размывание струйки происходит вследствие интенсивного об­разования вихрей и беспорядочного движения частиц жидкости. Та­кой режим движения жидкости называется турбулентным (рис. 3.2, в).

На практике имеет место как ламинарное, так и турбулентное движение. Ламинарный режим наблюдается, когда по трубам движутся весьма вязкие жидкости, например смазочные масла. Турбулентный режим – при движении маловязких жидкостей – воды, бензина, кислот и др. Переход от одного режима движения жидкости к другому происходит при определенном значении скорости v_кр, которая по­лучила название критической.

Рейнольдсом дан метод установления характера течения жидкос­ти через количественный критерий. Опыты показали, что режим дви­жения жидкости определяется комплексом следующих величин: ди­намической вязкостью m; плотностью жидкости r; средней скоростью потока v; величиной диаметра трубы, а количествен­ный критерий, названный в честь его автора числом Рейнольдса, имеет вид:

,

(3.1)

где u – кинематический коэффициент вязкости.

Число Рейнольдса, подсчитанное по критической скорости v_кр, называется критическим числом Рейнольдса,

.

(3.2)

Как показывают опыты, Re_кр для труб круглого сечения равен 2320. Если число Рейнольдса в потоке меньше 2320, течение ла­минарное, если больше – турбулентное.

Смена режима движения при достижении Re_кр обусловлена тем, что одно течение теряет устойчивость, а другое – приобретает. При Re < Re_кр ламинарное течение вполне устойчивое, а всякого рода турбулизация погашается влиянием вязкости. При Re > Re_кр, наобо­рот турбулентное течение устойчиво.

 

3.2. Понятие о гидродинамическом подобии

Сложность процессов, протекающих в жидкости не позволяет в полной мере использовать результаты теоретического анализа для решения практических задач, поэтому в гидравлике широко используется эксперимент в сочетании с теорией. Очевидно, что при постановке эксперимента возникает нужда в исследовании не натурных образцов гидравлических сооружений и устройств, а мо­делей этих устройств. При создании и исследовании моделей воз­никают такие вопросы: какие явления и процессы подобны изучаемому; что измерять при проведении эксперимента; как обрабаты­вать результаты исследования. Ответы на эти и другие вопросы дает наука о постановке эксперимента – теория подобия.

Подобными явлениями называются явления качественно одина­ковые, описываемые одинаковыми дифференциальными уравнениями. Гидродинамическое подобие – это подобие геометрическое, кинема­тическое и динамическое.

Геометрическое подобие означает пропорциональность сходст­венных размеров и равенство соответствующих углов: ; ; .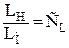

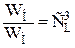Кинематическое подобие – это подобие линий тока и пропорциональность сходственных скоростей, ускорений: ; ; .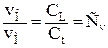

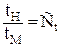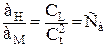Динамическое подобие – это подобие масс, плотностей, сил: ; ; .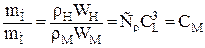

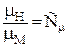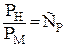Здесь индексы Н относятся к натурному потоку, М – к мо­дельному, соответственно L – линейный размер; F – площадь; W – объем; v – скорость; t – время; a – ускорение; m – масса; r – плотность; m – динамический коэффи­циент вязкости; Р – сила; С – масштаб моделирования.

Получим основной критерий гидродинамического подобия. В соответствии с законом Ньютона Р = m а. Для подобных потоков

(3.3)

или

.

(3.4)

Имея в виду значения масштабов моделирования, можно записать:

.

(3.5)

Поскольку комплексы (3.5) для подобных потоков должны быть одинаковыми, запишем:

.

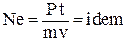(3.6)

Чаще пользуются другим выражением. Так как t = L/v, то

.

(3.7)

Полученный комплекс (3.7) называется критерием Ньютона.

Согласно первой теореме теории подобия подобные между собой явления имеют одинаковые критерии: Ne_н = Ne_м .

Вторая теорема подобия утверждает, что интеграл дифферен­циального уравнения, описывающего процесс движения жидкости, может быть представлен в виде зависимости между критериями подобия: f (k₁, k₂, k₃ …) = 0.

Если результаты опыта представить в критериальной форме, то эти критериальные зависимости будут общими для всех подоб­ных явлений.

Для получения общего гидродинамического подобия необходимо иметь подобие по всем силам, действующим в системе. Однако это не всегда возможно. В таких случаях пользуются частичным (локальным) подобием по силам, преобладающим в изучаемом пото­ке. При этом критерий Ne преобразуется в другие критерии.

Пусть в потоке преобладают силы трения. Тогда в соответ­ствии с законом

Ньютона

.

(3.8)

Подставим в критерий Ньютона вместо Р силу трения Т и получим:

.

(3.9)

В подобных системах 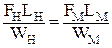, поэтому

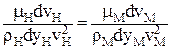
(3.10)

или

.

(3.11)

Запишем выражение (3.11) через масштабы моделирования:

.

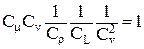(3.12)

Помня о том, что С_m /С_r = С_u, уравнение (3.12) примет вид:

.

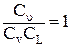(3.13)

Следовательно,

.

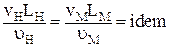(3.14)

Комплекс (3.14) назван критерием Рейнольдса и для подобных потоков, в которых главную роль играют силы трения

.

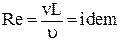(3.15)

Для круглой трубы характерным линейным размером является диаметр d и

.

(3.16)

Если в потоке преобладают силы тяжести, то в качестве силы Р в критерий Ньютона следует подставить G = mg:

.

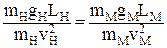(3.17)

После очевидных сокращений получим:

.

(3.18)

Отношение, обратное уравнению (3.18), называется критерием Фруда:

.

(3.19)

Следовательно, в тех случаях, когда моделируются явления, при которых преобладают силы тяжести, должно соблюдаться равенство критериев Фруда натуры и модели.

Если в жидкости преобладают силы давления, то в критерий Ньютона подставляют Р=DрF. После несложных преобразований получают критерий Эйлера

.

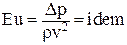(3.20)

В подобных потоках требуется равенство критериев Эйлера для натуры и модели: Eu_н = Eu_м.

С физической точки зрения все полученные критерии представляют собой меру отношения сил инерции к преобладающим в потоке жидкости силам.

Современная теория подобия рекомендует все результаты экспериментов
представлять в виде критериальной зависимости: Еu = f (Re, Fr).

Покажем, что коэффициент сопротивления l в формуле для расчета потерь напора по длине тоже является критерием подобия. Докажем это положение. Так как 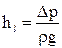, то после несложных преобразований получим:

,

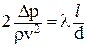(3.21)

или

.

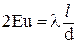(3.22)

Ниже убедимся в том, что l = f (Re), и тогда получим, что

,

(3.23)

а это согласуется с требованиями теории подобия.

 

 

4. Ламинарное движение жидкости

 

4.1. Потери на трение при равномерном движении

 

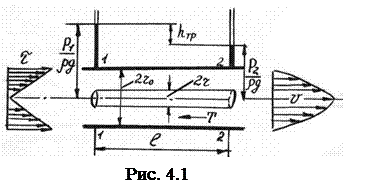При исследовании любого режима движения, в том числе ламинарного, ставится задача расчета потерь напора и поля скоростей. Рассмотрим установившееся равномерное движение жидкости в круглой цилиндрической трубе (рис. 4.1).

 

В соответствии с уравнением Бернулли

.

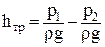(4.1)

Выделим в движущейся жидкости объем диаметром 2r и длиной l. Запишем уравнение равномерного движения выделенного объема:

P1 – P2 – T = 0,

(4.2)

где Р₁ = p₁ pr² – сила давления на сечение 1–1;

р₂ = p₂ pr² – сила давления на сечение 2–2;

Т = 2pr l t – сила трения, действующая на поверхности цилиндра;

t – касательное напряжение.

Подставим значения Р₁, Р₂, Т в уравнение (4.2):

(p1 – p2) pr2 – 2pr l t = 0.

(4.3)

Отсюда

,

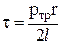(4.4)

где p_тр = p₁ – p₂ – потеря давления между сечениями 1–1 и 2–2.

Таким образом, устанавливается закон распределения каса­тельного напряжения по сечению потока. Закон этот линейный и свидетельствует о том, что в центре потока, когда r = 0, t = 0, а на стенке r = r₀, t = t_max = 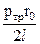. Эпюра касательного напряжения показана на рис. 4.1.

4.2. Поле скоростей и потери напора при ламинарном

режиме движения жидкости

Для получения закона распределения скоростей по сечению потока запишем в соответствии с законом Ньютона:

.

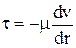(4.5)

Знак «минус» в правой части уравнения (4.5) обусловлен тем, что скорость от центра к стенке убывает, следовательно, градиент скорости имеет
отрицательное значение. Приравниваем выражение (4.4) к (4.5):

,

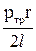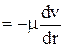(4.6)

разделим переменные:

;

(4.7)

возьмем интеграл:

.

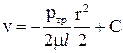(4.8)

Для определения постоянной интегрирования С подставим в уравнение (4.8) граничные условия: r = r₀, v = 0 (условия прили­пания жидкости к стенке), тогда

.

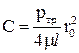(4.9)

Отсюда получим закон распределения скоростей по сечению потока:

.

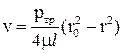(4.10)

Уравнение (4.10) представляет собой параболоид вращения, т. е. при
ламинарном режиме имеем параболический закон распределе­ния скоростей.
В центре трубопровода, когда r = 0, скорость имеет максимальное значение:

,

(4.11)

а на стенке, где r = r₀, скорость равна нулю.

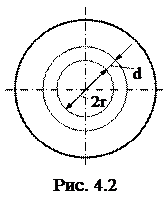Применим полученный закон распределения скоростей для рас­чета расхода. Рассмотрим элементарное кольцо толщиной dr (рис. 4.2). Рас­ход жидкости через это кольцо

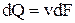
(4.12)

или, так как dF = 2prdr,

.

(4.13)

Возьмем интеграл по всему сечению трубопровода:

,

(4.14)

найдем среднюю по сечению скорость:

.

(4.15)

Сравнив среднюю скорость с максимальной, убеждаемся в том, что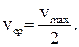

Определим значение коэффициента l. Из уравнения (4.15) имеем

.

(4.16)

Умножим и разделим правую часть уравнения (4.16) на 2v_cp; кроме того, запишем, что р_тр = rgh_тр, тогда,

.

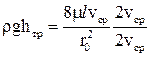(4.17)

Заменим в выражении (4.17) m/r = u и 2r₀ = d₀, получим:

.

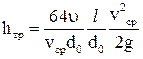(4.18)

Если сравнить уравнение (4.18) с общей формулой для расчета потерь по длине 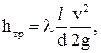можно убедиться в том, что для ламинарного режима

.

(4.19)

Зная закон распределения скоростей, получим значение коэффициента a для ламинарного режима:

.

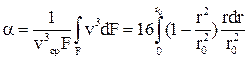(4.20)

Обозначим 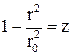, тогда

.

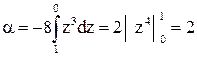(4.21)

Итак, полученная кинетическая энергия ламинарного потока с параболическим распределением скоростей в два раза превышает кинетическую энергию, подсчитанную по средней скорости.

Изложенная теория хорошо подтверждается опытом, за исклю­чением следующих случаев: при течении на начальном участке трубы, где формируется поле скоростей; при течении со значительным теплообменом, так как неизотермичностъ существенно искажает поле скоростей.

 

 

5. Турбулентное движение жидкости

 

5.1. Природа потерь при турбулентном движении

 

Турбулентный режим движения жидкости наиболее часто встре­чается в природе и технике и отличается чрезвычайной сложностью происходящих в нем процессов. Естественно, что сложность процессов не позволяет разработать строгую теорию турбулентного дви­жения. При теоретическом анализе вводятся разного рода упрощен­ные модели, а результаты теоретических расчетов уточняются пу­тем сопоставления их с результатами экспериментов.

Бесспорным является факт интенсивного перемешивания частиц жидкости. Если поместить в турбулентный поток весьма чувствитель­ный прибор для измерения скорости, то окажется, что в данной точке скорость с течением времени будет меняться (рис. 5.1).

Траектории частиц, проходящих через данную точку, представ­ляют собой кривые различной формы, значит, турбулентное течение является неустановившимся. В силу того, что непрерывно происходит перемешивание жидкости и обмен коли

Поделиться:

Воспользуйтесь поиском по сайту: