Экспериментальное изучение свойств материала при растяжении. Основные механические характеристики материала
Основным видом испытаний конструкционных материалов для оценкиих механических свойств является испытание на центральное одноосное растяжение. Одноосное растяжение сравнительно легко подвергается анализу, позволяет по результатам одного опыта определить сразу несколько важных механических характеристик материала, необходимых для конструкторских расчетов. Результаты опыта отображаются на специальном графике - диаграмме растяжения.
Методы испытания на растяжение стандартизованы, например, ГОСТ 1497-84 «Металлы. Методы испытаний на растяжение» для испытаний на растяжение при температуре 20°С. Имеются отдельные стандарты на испытания при повышенных до 1473º К и пониженных от 273° до 173º К температурах. Регламентированы форма, размеры образцов, основные требования к испытательному оборудованию, методика проведения испытания и обработки его результатов.
На рис. 3.6 показан наиболее часто используемый стандартный образец для исследования при комнатной температуре. Помимо рабочей части (l) образцы имеют торцевые головки различной конфигурации для крепления в испытательных машинах.
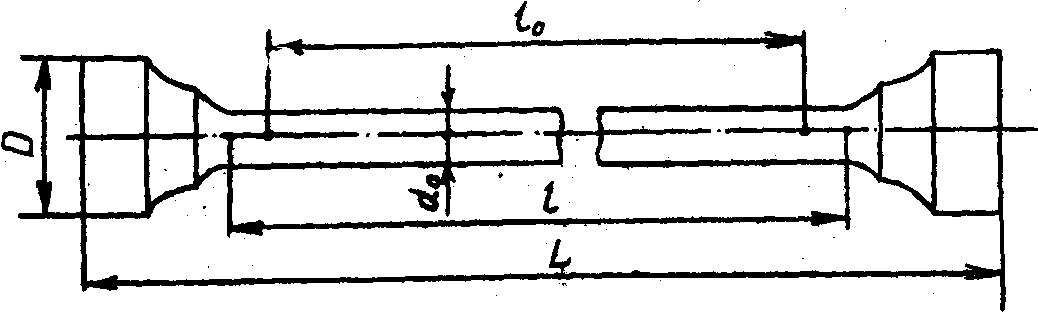
Рис. 3.6. Стандартный образец для испытаний на растяжение
Основные размеры образца:
- рабочая длина l - часть образца между его головками или участками для захвата с постоянной площадью поперечного сечения;
- начальная расчетная длина l o - участок рабочей длины, на котором определяется удлинение;
- начальный диаметр рабочей части d o - для цилиндрических образцов или начальная толщина d o и ширина b o рабочей части - у плоских образцов.
Между размерами образца должны существовать определенные соотношения. В частности, для цилиндрических образцов l ³ l o+ d o, для плоских l ³ l o+ b o /2. Расчетная длина составляет  , где F o - начальная площадь поперечного сечения в рабочей части образца. Для цилиндрического образца это равносильно тому, что l o = 10 d o. Цилиндрические образцы с d o = 10мми l o = 100ммсчитаются основными. Образцы всех остальных диаметров называются пропорциональными.
, где F o - начальная площадь поперечного сечения в рабочей части образца. Для цилиндрического образца это равносильно тому, что l o = 10 d o. Цилиндрические образцы с d o = 10мми l o = 100ммсчитаются основными. Образцы всех остальных диаметров называются пропорциональными.
В некоторых случаях, например, при работе с малогабаритными изделиями или дефицитными материалами, возникает необходимость в определении свойств образцов, меньших по размерам, чем установлено стандартами. Такие "микрообразцы" могут иметь d o £ 1мм, l o = 4-7 мм.
Испытание образца осуществляется на разрывной машине с записывающим устройством, автоматически вычерчивающим диаграмму растяжения (график, связывающий нагрузку и деформацию образца в процессе его растяжения до момента разрыва).
На рис. 3.7 показана диаграмма растяжения пластичного материала - малоуглеродистой стали. На оси абсцисс откладывается абсолютное удлинение образца Δl, по оси ординат - сопротивление образца, т.е. нагрузка Р, соответствующая этому удлинению.
Прямолинейный участок диаграммы ОА указывает на пропорциональность между удлинением и нагрузкой (выполняется закон Гука). Нарушение этой пропорциональности при дальнейшем нагружении образца из малоуглеродистой стали сопровождается текучестью материала - возрастанием удлинения при почти постоянной нагрузке. Текучести на диаграмме соответствует горизонтальный участок АВ, часто называемый площадкой текучести. Напряжение, соответствующее этой площадке, называется пределом текучести и обозначается s т. Предел текучести s т определяется как
 ,
,
где P т - нагрузка, соответствующая текучести материала образца; Fo. - начальная площадь поперечного сечения образца.
Рис. 3.7. Диаграмма растяжения пластичного материала - малоуглеродистой стали
При дальнейшем нагружении после стадии текучести материал вновь сопротивляется возрастающим деформациям, наступает так называемая стадия упрочнения (кривая ВС). При максимальной нагрузке Ртах в образце из малоуглеродистой стали начинает образовываться местное сужение поперечного сечения - шейка, вследствие чего сопротивление образца при дальнейшем растяжении быстро падает, и кривая CD диаграммы идет вниз. Точка D соответствует разрушению образца.
Условное напряжение, полученное как частное от деления максимальной нагрузки Рmax на первоначальную площадь поперечного сечения образца Fo, называется временным сопротивлением или пределом прочности материала.
 .
.
Нагрузка P разр, соответствующая точке D, меньше Ртах. Но истинное напряжение s разр, получающееся при делении нагрузки P разр на минимальную площадь A 1 в поперечном сечении шейки образца, возрастает
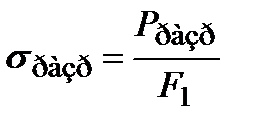 .
.
К моменту разрыва истинное напряжение в шейке имеет наибольшее значение: оно может в два или даже в три раза превышать временное сопротивление.
Для других материалов диаграмма растяжения может не содержать ярко выраженной площадки текучести, как показано на рис. 3.8.
Рис. 3.8. Диаграмма растяжения для легированной стали и алюминиевого сплава
Если во время испытания, начиная с некоторой точки диаграммы К, будем разгружать образец (показано стрелками), то диаграмма пойдет по прямой KL, параллельной ОА (рис. 3.9).
Рис. 3.9. Диаграмма растяжения при разгрузке образца
Отрезок OL равен остаточному удлинению Δlост, соответствующему точке К, а отрезок LM - упругому удлинению Δlупр, соответствующему той же точке. В результате полное удлинение в точке К определяется как сумма двух указанных удлинений Δl = Δlост + Δlупр. Упругое удлинение (прямая KL) подчиняется закону Гука. Если после разгрузки снова приложить растягивающую силу, то на диаграмме повторится та же прямая LK, но в обратном направлении, и при дальнейшем нагружении получим кривую LКСD, являющуюся как бы продолжением предыдущей диаграммы (рис. 3.10б). Положим теперь, что имеются два одинаковых образца, изготовленных из одного и того же материала. Один из образцов до испытания нагружению не подвергался, а другой был предварительно нагружен силами, вызывавшими в образце остаточные деформации. Испытывая первый образец, получим диаграмму растяжения, показанную на рис. 3.10а. При испытании второго образца отсчет удлинения будет производиться, естественно, от ненагруженного состояния, которому на рис. 3.10а соответствует точка L. Поэтому остаточное удлинение OL учтено не будет. В результате получаем диаграмму LKCD (рис. 3.10б) без площадки текучести. Весьма существенным является то, что отрезок LK оказывается длиннее отрезка ОА, т.е. в результате предварительной натяжки материал приобретает способность воспринимать большие нагрузки без остаточных деформаций (в упругой области). Подобная технологическая операция по предварительному нагружению с образованием Δlост называется нагартовкой (наклеп).
Рис. 3.10. Диаграмма растяжения при разгрузке образца
Одной из важнейших характеристик материала является предел пропорциональности. Стандартизован способ графического определения предела пропорциональности по диаграмме растяжения (рис. 3. 11).
Рис. 3.11. Графическое определение предела пропорциональности
Для этого из начала координат проводят прямую ОМ, совпадающую с начальным линейным участком диаграммы. Затем на произвольном уровне проводят прямую АВ, параллельную оси абсцисс, и на прямой откладывают отрезок kn, равный половине отрезка mk. Через точку n и начало координат проводят прямую Оn и параллельно ей проводят касательную CD к диаграмме растяжения. Точка касания определяет искомое усилие РПЦ.
Тогда предел пропорциональности материала равен  .
.
Ряд материалов при растяжении дает диаграмму без выраженной площадки текучести. На рис. 3.12 приведен пример такой диаграммы. Для подобных материалов вместо предела текучести σ т устанавливается так называемый условный предел текучести σ 0,2=Р0,2/F0. Он определяется как величина напряжения, при котором остаточная деформация ε ост=0.002 (или ε ост=0.2%). К материалам, для которых определяется условный предел текучести, относится дуралюмин, бронза, высокоуглеродистые и легированные стали.
Рис. 3.12. Определение условного предела текучести
Условный предел текучести можно определить графически по диаграмме растяжения, имеющей достаточно большой масштаб (не менее 10:1 по оси деформаций). Для этого по указанной оси от начала координат откладывают отрезок OL, которому соответствует ε=Δl/l0=0.002, и через точку L проводят прямую параллельную прямолинейному участку диаграммы ОA. Ордината точки К соответствует величине нагрузки Р 0,2.
Способность материала разрушаться при незначительных остаточных деформациях называется хрупкостью. Для таких материалов величина остаточного удлинения при разрыве не превышает 2-5%, в ряде случаев измеряется долями процентов. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, углепластики, стеклопластики и др.
Следует отметить, что деление материалов на пластичные и хрупкие является условным, так как в зависимости от условий испытания (скорость нагружения, температура) и вида напряженного состояния хрупкие материалы способны вести себякак пластичные, а пластичные- как хрупкие. Например, чугунный образец в условиях всестороннего сжатия ведет себя как пластичный материал, т.е. не разрушается даже при значительных деформациях. И напротив, стальной образец с выточкой разрушается при сравнительно небольших деформациях. Таким образом, правильнее говорить о пластичном и хрупком состояниях материала.
При растяжении образцов из хрупкого материала отклонение от закона Гука начинается очень рано. Разрыв наступает внезапно, при малых деформациях и без образования шейки. При испытании на растяжение хрупких материалов определяют, как правило, только, предел прочности σ в =Рmax/F o.
Для сравнения результатов испытаний образцов различных размеров, изготовленных из одинаковых материалов, изображают условную диаграмму растяжения в системе координат “напряжение - относительное удлинение”. По оси ординат откладывают значение соответствующего нормального напряжения в поперечном сечении растягиваемого образца σ = Р/F o, где Fo - первоначальная площадь сечения образца, а по оси абсцисс - относительное удлинение образца ε=Δl/l o, где l o - его первоначальная длина.
Эту диаграмму называют условной диаграммой растяжения или диаграммой условных напряжений, так как напряжения и деформации вычисляются соответственно по отношению к первоначальной площади F o и первоначальной длине образца l o.
На рис. 3.13 приведена условная диаграмма растяжения образца из малоуглеродистой стали (сплошная линия). Как видно, на участке ОА до наступления напряжения σ пц деформации растут пропорционально напряжениям. До предела пропорциональности сохраняет силу закон Гука. При дальнейшем увеличении нагрузки диаграмма становится криволинейной.
Диаграмма растяжения, построенная с учетом изменения площади поперечного сечения и местного удлинения, называется истинной диаграммой растяжения (штриховая кривая ОАВ'С'D', рис. 3.13).
Рис. 3.13. Условная и истинная диаграммы растяжения
К механическим характеристикам относят также модуль Юнга E и коэффициент Пуассона µ, характеризующие соответственно продольную и поперечную деформации материала при растяжении. Их определяют экспериментально при помощи тензометров (измерителей деформации) различной конструкции.
При увеличении температуры материала его механические характеристики изменяются. Как правило, характеристики прочности (напряжения σ в, σ т и др.) и характеризующий жесткость при растяжении модуль Юнга уменьшаются при нагревании.
Воспользуйтесь поиском по сайту:



 , где F o - начальная площадь поперечного сечения в рабочей части образца. Для цилиндрического образца это равносильно тому, что l o = 10 d o. Цилиндрические образцы с d o = 10мми l o = 100ммсчитаются основными. Образцы всех остальных диаметров называются пропорциональными.
, где F o - начальная площадь поперечного сечения в рабочей части образца. Для цилиндрического образца это равносильно тому, что l o = 10 d o. Цилиндрические образцы с d o = 10мми l o = 100ммсчитаются основными. Образцы всех остальных диаметров называются пропорциональными. ,
, .
.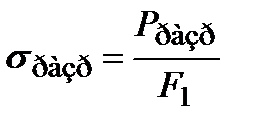 .
. .
.

