Определение напряжений в поперечных сечениях
При поперечном изгибе в сечениях балки от поперечной силы Q возникают касательные напряжения и соответствующие угловые деформации γ, как это было показано при сдвиге, а от действия изгибающего момента М – нормальные напряжения (чистый изгиб). Наличие угловых деформаций приводит к искажению сечений, они в процессе деформации уже не остаются плоскими. Так как поперечная сила не равна нулю, то в соответствии с зависимостью (10.2) изгибающий момент изменяется по длине балки, а значит, изменяется и текущая кривизна упругой линии. Кроме того, при переменной поперечной силе уже и в продольных сечениях балки возникают нормальные напряжения. Указанные особенности влияют на НДС балки при поперечном изгибе.
Однако аналитические исследования методами теории упругости и многочисленные эксперименты показывают, что в первом приближении при исследовании НДС балки при поперечном изгибе можно использовать зависимости, полученные при анализе чистого изгиба:
 ;
;  ;
; 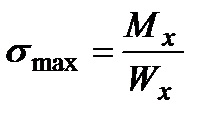 . (10.3)
. (10.3)
Рассмотрим определение касательных напряжений в частном случае балки прямоугольного поперечного сечения (рис. 10.3). Выделим элемент баки длиной dz.
Рис. 10.3. Напряжения при поперечном изгибе
Изгибающие моменты, действующие в левом и правом сечениях, отличаются на величину dMx, что следует из условия равновесия данного элемента. Важно отметить, что так как на участке балки длиной dz нет внешних поперечных сил, то на данном участке Qy=const. Продольным горизонтальным сечением (точечные линии на рис. 10.3а), удаленным от нейтрального слоя на расстояние y, разделим рассматриваемый элемент на две части и рассмотрим верхнюю часть (рис. 10.3б). На данном рисунке: y1- координата текущего сечения в верхней части элемента; F* - площадь «отсеченной части» поперечного сечения; dσ – приращение нормальных напряжений при переходе от левого сечения к правому. Очевидно, что разница продольных усилий (от нормальных напряжений) в поперечных сечениях элемента балки может быть компенсирована только соответствующими касательными напряжениями τ.
Составим условия равновесия выделенной части элемента балки (от сечения с координатой y1, то h/2)
 . (10.4)
. (10.4)
Откуда
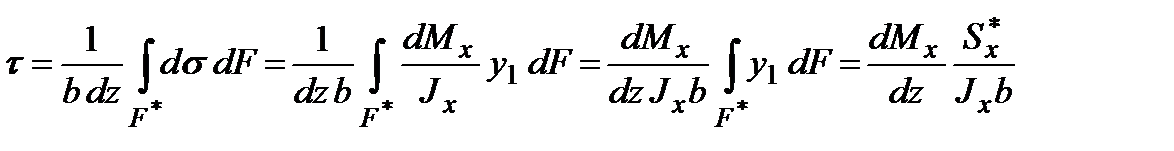 ;
; 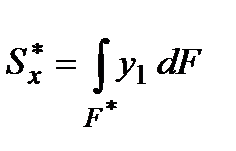 , (10.5)
, (10.5)
где  - статический момент отсеченной части элемента, т.е. части, находящейся выше продольного сечения с координатой y1; Jx – момент инерции сечения относительно главной центральной оси Ox; b- ширина сечения балки в продольном сечении, удаленном на расстояние y от нейтрального слоя (очевидно, что в данном примере с сечением прямоугольной формы b=const по высоте всего сечения).
- статический момент отсеченной части элемента, т.е. части, находящейся выше продольного сечения с координатой y1; Jx – момент инерции сечения относительно главной центральной оси Ox; b- ширина сечения балки в продольном сечении, удаленном на расстояние y от нейтрального слоя (очевидно, что в данном примере с сечением прямоугольной формы b=const по высоте всего сечения).
Учитывая дифференциальную зависимость между изгибающим моментом и поперечной силой (10.2), получим окончательно
 . (10.6)
. (10.6)
Предположим, что касательные напряжения τ параллельны оси Oz, постоянны по длине dz и ширине b. вычисленные по формуле (10.6) касательные напряжения действуют в продольных сечениях элемента балки, но по закону парности касательных напряжений такие же напряжения, параллельные силе Q, будут действовать в поперечных сечениях.
Отметим, что результат не изменится, если между поперечными сечениями на длине dz будет действовать распределенная нагрузка интенсивностью q. Это объясняется следующим: в процессе вывода формулы (10.6) вычислялись касательные напряжения в горизонтальном сечении элемента, которые зависят лишь от разности изгибающих моментов в левом и правом сечении, и их можно считать постоянными по длине dz, а добавочным моментом от q можно пренебречь, как величиной второго порядка малости.
Формула (10.6) была получена Д.И. Журавским и носит его имя. Положенные в основу вывода допущения строго подтверждаются лишь для узких прямоугольных сечений (h/b>2), но, как показывает практика расчетов, данной формулой можно пользоваться в большинстве случаев балок прямоугольного поперечного сечения.
Формула Журавского может быть использована и для определения касательных напряжений при расчете балок произвольного поперечного сечения на поперечный изгиб. В этом случае смысл всех параметров, входящих в формулу (10.6) не меняется, а b(y) в этом случае текущая ширина продольного сечения, в котором вычисляются касательные напряжения (рис. 10.4)
Рис. 10.4. Поперечный изгиб балки произвольного сечения
Отметим, что по формуле Журавского в случае произвольного поперечного сечения балки можно определить лишь значение касательных напряжений, параллельных поперечной силе Qy и направленных в сторону ее действия. Однако при переменной ширине сечения возникают составляющие касательного напряжения, направленные вдоль оси Ox. Это связано с возможностью доказать, как это сделано при изучении кручения вала, что вблизи внешнего контура касательные напряжения должны быть направлены по касательной к контуру в рассматриваемой точке. Значит предположение о постоянстве касательных напряжений по ширине сечения не совсем справедливо. Однако более точные исследования и практика расчетов показывает, что составляющей касательных напряжений вдоль оси Ох в первом приближении можно пренебречь.
Воспользуйтесь поиском по сайту:


 ;
;  ;
; 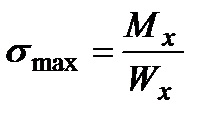 . (10.3)
. (10.3) . (10.4)
. (10.4)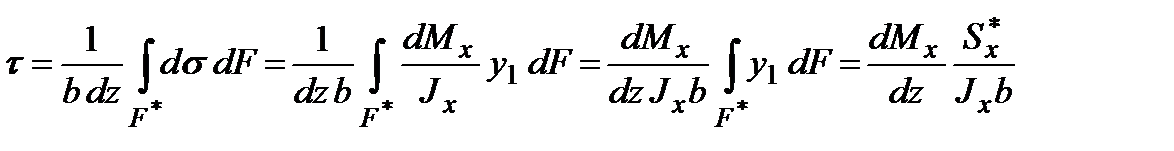 ;
; 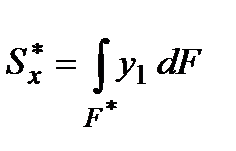 , (10.5)
, (10.5) - статический момент отсеченной части элемента, т.е. части, находящейся выше продольного сечения с координатой y1; Jx – момент инерции сечения относительно главной центральной оси Ox; b- ширина сечения балки в продольном сечении, удаленном на расстояние y от нейтрального слоя (очевидно, что в данном примере с сечением прямоугольной формы b=const по высоте всего сечения).
- статический момент отсеченной части элемента, т.е. части, находящейся выше продольного сечения с координатой y1; Jx – момент инерции сечения относительно главной центральной оси Ox; b- ширина сечения балки в продольном сечении, удаленном на расстояние y от нейтрального слоя (очевидно, что в данном примере с сечением прямоугольной формы b=const по высоте всего сечения). . (10.6)
. (10.6)

