Модели нагрузок. Силы и их классификация
Внешние силы (нагрузки), действующие на деформируемое тело, принято делить на:
- статические (стационарные) и динамические (нестационарные) (т.е. независящие и зависящие от времени);
- поверхностные и объемные;
- сосредоточенные и распределенные.
По характеру приложения во времени нагрузки подразделяются на статические и динамические. Нагрузки, медленно изменяющиеся по времени от нуля до своего конечного значения, называются статическими; силами инерции здесь пренебрегают. Условие статического нагружения
 ,
,
где  — время нарастания нагрузки;
— время нарастания нагрузки; 
 - период низшего тона собственных колебаний конструкции;
- период низшего тона собственных колебаний конструкции;  — низшая круговая частота собственных колебаний конструкции.
— низшая круговая частота собственных колебаний конструкции.
Динамические нагрузки сопровождаются значительными ускорениями точек деформируемого тела. При этом возникают силы инерции, которыми пренебречь нельзя. Динамические нагрузки делят на мгновенно приложенные, ударные и повторно-переменные.
Нагрузка считается мгновенно приложенной или быстро приложенной, если она возрастает в течение короткого промежутка времени:
 .
.
Авиационные конструкции многоразового пользования подвергаются, как правило, действию переменных нагрузок, называемых повторно-переменными.
Объемные силы действуют непрерывно по всему объему тела. Примерами объемных сил могут служить силы тяжести, центробежные силы, электромагнитные силы и силы инерции. Поверхностные силы приложены к точкам поверхности тела и являются результатом взаимодействия твердых тел или воздействия на них внешней среды, например, набегающего потока воздуха на крыло ЛА (воздушная нагрузка).
Часто нагрузку, распределенную по поверхности р (рис. 1.5 а), приводят к главной плоскости, в результате чего получается нагрузка q, распределенная по линии или погонная нагрузка (рис. 1.5 б). Очевидно, что размерность распределенной по площади нагрузки Н/м2, а погонной – Н/м. Иногда в технической литературе погонную нагрузку q называют распределенной, в том смысле, что она распределена по длине конструктивного элемента.
Рис.1.5. Распределенная (а) и погонная (б) нагрузки

Иногда возникает необходимость приведения распределенной по поверхности или погонной нагрузки к эквивалентной сосредоточенной силе. При этом абсолютное значение эквивалентной силы равно площади эпюры (графика изменения распределенной нагрузки по длине элемента конструкции) распределенной нагрузки и приложена она в центре тяжести этой эпюры. Так, на рис. 1.6 показаны схемы перехода от реально действующей погонной нагрузки к эквивалентной силе Рэкв для двух простейших случаев: равномерной погонной нагрузки и нагрузки, распределенной по линейному закону. Очевидно, что такой переход допустим лишь в том случае, если длина участка действия погонной нагрузки l существенно меньше длины всего объекта в целом L, как это показано на рис. 1.7. Встречаются нагрузки, которые могут быть представлены в виде сосредоточенного момента 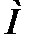 (пары сил) (размерность H·м).
(пары сил) (размерность H·м).
Все реально действующие внешние нагрузки распределены по некоторому конечному участку тела. Тем не менее, при схематизации реальных объектов (например, узлов крепления) в сопротивлении материалов делаются упрощения в системе сил, приложенных к элементу конструкции. Смысл упрощения, при котором вводится понятие сосредоточенной силы, ясен из рис.1.7 (при  сила
сила  , действующая в узле крепления груза считается сосредоточенной). Аналогично может быть рассмотрено введение понятия сосредоточенного момента.
, действующая в узле крепления груза считается сосредоточенной). Аналогично может быть рассмотрено введение понятия сосредоточенного момента.
Рис.1.6. Схема перехода к эквивалентной нагрузке

Рис. 1.7. К выбору представления силы в расчетной схеме
Модели опор
Опорные устройства (связи) препятствуют тем или иным перемещениям тела или вообще исключают их. Опорные устройства классифицируются по числу накладываемых на объект связей (ограничений). Если нет специальных указаний, опорные связи и поверхности считаются абсолютно жесткими. При нагружении тела на него со стороны опорных связей (поверхностей) действуют силы, называемые опорными реакциями. Для плоского тела (в частности, бруса) основными видами опор являются: шарнирно-неподвижная (рис. 1.8), шарнирно-подвижная (рис. 1.9) и защемление (рис. 1.10). На этих же рисунках показаны реакции в таких опорах.
Количество этих реакций, которые обычно относят к внешним нагрузкам, определяется количеством исключенных перемещений. При «запрете» линейного смещения в опоре возникает сила по направлению этого смещения (на рисунках Rx, Ry), при запрете углового смещения возникает момент (на рисунке M).
При действии внешних нагрузок на тело силы взаимодействия между его частицами получают некоторые приращения, которые называются внутренними силами или усилиями. Именно они, как будет ясно из дальнейшего, определяют прочность элемента конструкции. Расчетное определение внутренних усилий – одна из основных задач сопротивления материалов.
Для нахождения реакций опор и внутренних усилий составляют уравнения равновесия тела и его частей. Как известно из теоретической механики, таких уравнений для каждой мысленно выделенной части упругого тела можно составить 3 на плоскости и 6 в пространстве.


Рис. 1.8. Шарнирно-неподвижная опора Рис. 1.9. Шарнирно-подвижная опора
Рис. 1.10. Защемление (заделка)
В зависимости от соотношения числа уравнений статики (N у) и неизвестных (N н) в этих уравнениях реакций опор можно провести следующую классификацию упругих систем.
1. N у> N н - геометрически изменяемая система или механизм. Для исследования такой системы необходимы уравнения динамики, в которые войдут ускорения системы (рис. 1.11, где N у=3, N н=2).
Рис. 1.11. Геометрически изменяемая система
2. N у= N н - геометрически неизменяемая статически определимая система (рис. 1.12а, где N у= N н=3).
3. N у< N н - геометрически неизменяемая статически неопределимая система (рис. 1.12б, где N у=3, N н=4) Для исследования такой системы необходимо уравнения статики дополнить так называемыми уравнениями совместности деформаций, которые будут рассматриваться ниже.
Рис. 1.12. Геометрически неизменяемые системы
Воспользуйтесь поиском по сайту:


 ,
, — время нарастания нагрузки;
— время нарастания нагрузки; 
 - период низшего тона собственных колебаний конструкции;
- период низшего тона собственных колебаний конструкции;  — низшая круговая частота собственных колебаний конструкции.
— низшая круговая частота собственных колебаний конструкции. .
.
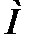 (пары сил) (размерность H·м).
(пары сил) (размерность H·м). сила
сила  , действующая в узле крепления груза считается сосредоточенной). Аналогично может быть рассмотрено введение понятия сосредоточенного момента.
, действующая в узле крепления груза считается сосредоточенной). Аналогично может быть рассмотрено введение понятия сосредоточенного момента.


