 |
Схема оценки корреляционной связи по коэффициенту корреляции
|
|
|
|
Самостоятельная Работа Студента
Специальность: ОМ
Дисциплина: Общественное Здравоохранение
Кафедра: общественного здравоохранения
Курс: 3
Группа: 320 «А»
Тема: Вычисление критериев корреляции
Форма выполнения: Реферат
Выполнил: Бекенов Т.
Проверила: Ермуханова Л.С.
Актобе 2017
При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.
1. Виды проявления количественных связей между признаками
o функциональная связь
o корреляционная связь
Определения функциональной и корреляционной связи
Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
|
|
|
Практическое значение установления корреляционной связи. Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
Величина, характеризующая направление и силу связи между признаками. Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1
Способы представления корреляционной связи
o график (диаграмма рассеяния)
o коэффициент корреляции
Направление корреляционной связи
o прямая
o oбратная
Сила корреляционной связи
o сильная: ±0,7 до ±1
o средняя: ±0,3 до ±0,699
o слабая: 0 до ±0,299
Методы определения коэффициента корреляции и формулы
o метод квадратов (метод Пирсона)
o ранговый метод (метод Спирмена)
Методические требования к использованию коэффициента корреляции
o измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
o расчет может производиться с использованием абсолютных или производных величин
o для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
o число наблюдений не менее 30
Рекомендации по применению метода ранговой корреляции (метод Спирмена)
|
|
|
o когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных
o когда признаки представлены не только количественными, но и атрибутивными значениями
o когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)
Рекомендации к применению метода квадратов (метод Пирсона)
o когда требуется точное установление силы связи между признаками
o когда признаки имеют только количественное выражение
Методика и порядок вычисления коэффициента корреляции
Метод квадратов
· построить вариационные ряды для каждого из сопоставляемых признаков, обозначив первый и второй ряд чисел соответственно х и у;
· определить для каждого вариационного ряда средние значения (М1 и М2);
· найти отклонения (dх и dy) каждого числового значения от среднего значения своего вариационного ряда;
· полученные отклонения перемножить (dx X dy)
· каждое отклонение возвести в квадрат и суммировать по каждому ряду (Σ dx2 и dy2)
· подставить полученные значения в формулу расчета коэффициента корреляции:

при наличии вычислительной техники расчет производится по формуле:
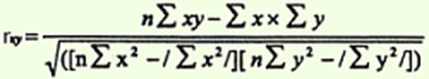
Ранговый метод
· составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют
· величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин
· определить разность рангов между х и у (d): d = х — у
· возвести полученную разность рангов в квадрат (d2)
· получить сумму квадратов разности (Σ d2) и подставить полученные значения в формулу:

Схема оценки корреляционной связи по коэффициенту корреляции
|
|
|
| Сила связи | Направление связи | |
| прямая (+) | обратная (-) | |
| Сильная | от + 1 до +0,7 | от - 1 до - 0,7 |
| Средняя | от + 0,699 до + 0,3 | от - 0,699 до - 0,3 |
| Слабая | от + 0,299 до 0 | от - 0,299 до 0 |
|
|
|


