Структурный анализ рычажного механизма.

 

Структурный анализ механизма можно выполнить в следующем порядке:

1) определить степень подвижности механизма и сравнить с числом ведущих звеньев;

2) выявить и исключить пассивные связи и лишние степени подвижности;

3) выполнить замену высших кинематических пар низшими и проверить степень подвижности заменяющего механизма;

4) разложить механизм на структурные группы, записать формулу строения механизма, определить класс механизма.

Рассмотрим этот порядок на примере кулачково-рычажного механизма рис.3, преобразующего вращательное движение кулачка 1 в возвратно-поступательное движение ползуна 5, которые соответственно являются ведущим и ведомым звеньями. Тогда, ролик 2, коромысло 3 и шатун 4 будут промежуточными звеньями.

 

Рис.3. Пример плоского механизма.

 

Степень подвижности плоского механизма можно найти по формуле Чебышева

 

(1.1)

где W – число степеней подвижности механизма,

, - количество одно- и двухподвижных кинематических пар,

n – число подвижных звеньев.

Формулу (1.1) можно записать в виде , где n – число подвижных звеньев, а Р₅ и Р₄ – число кинематических пар 5-ого и 4-ого классов.

На рис. 3 всего шесть звеньев, поэтому механизм называют шестизвенным. При этом подвижных звеньев пять: 1,2,3,4,5 и одно неподвижное 0-стойка. Таким образом, n=5.

Все кинематические пары на рис. 3 обозначены буквами: их 8. Кинематическая пара В-контакт кулачка с роликом – является двухподвижной, т.е. . Все остальные кинематические пары одноподвижные, но , а не семи. Дело в том, что кинематическая пара Н (или G) является дублером пары G (или Н) и не влияет на кинематику механизма. Она образует (называется) пассивную или избыточную связь.

Подставляем в формулу Чебышева n=5, и получаем W=2. Степень подвижности показывает число возможных ведущих звеньев. В данном примере ведущим звеном может быть только кулачок 1. Вторую степень подвижности дает местное вращение ролика 2, которое не влияет на кинематику механизма и называется лишней степенью подвижности. Т.е., если убрать вращательную кинематическую пару С и ролик 2 жестко соединить с коромыслом 3, то закон движения выходного звена 5 будет таким же, что и с вращающимся роликом и степень подвижности W будет равна единице. В данном случае вращение ролика позволяет уменьшить потери энергии на преодоление сил трения: трение скольжения в случае не вращающегося ролика заменяется трением качения в случае вращающегося ролика.

Теперь выполним замену высшей кинематической пары В низшими. Для этого в точке контакта профилей В проводим общую нормаль n-n и на ней находим центры кривизны профилей в точке контакта. Один центр кривизны совпадает с центром ролика С, а другой находится в точке К. Т.е., если из точки К радиусом КВ провести окружность, то в точке В и ее окрестности эта окружность будет совпадать с профилем кулачка *). На рис. 3 эта окружность проведена пунктиром и для наглядности чуть смещена. В эти центры кривизны помещаем шарниры и соединяем их между собой жестким звеном. Проверяем степень подвижности заменяющего механизма:

,

т.е. получаем ту же степень подвижности, что и должна быть без учета лишней степени подвижности.

Структурной группой называется кинематическая цепь с нулевой степенью подвижности

относительно элементов ее внешних пар, которая не распадается на более простые цепи, также обладающие нулевой степенью подвижности.

Механизм без высших кинематических пар можно разложить на структурные группы или группы Ассура. По правилу Л.В. Ассура любой плоский механизм может быть образован путем присоединения структурных групп к механизму 1-ого класса.

Механизм первого класса образуют подвижное звено и стойка, соединенные между собой

кинематической цепи. Тогда из формулы Чебышева при отсутствии высших кинематических пар получаем, что структурная группа может состоять только из четного числа звеньев и числа кинематических пар, кратного трем.

 

Рис. 4. Заменяющий механизм

 

_

^*) Если вместо одного из профилей будет прямая, то вместо шарнира ставят ползун, который жестко соединяют с центром кривизны второго профиля. Направляющей ползуна будет сама прямая.

 

 

Примеры структурных групп

1. n=2, P1=3. С таким набором звеньев и кинематических пар структурную группу принято называть структурной группой второго класса. Их 5 видов (рис. 5)

Рис.5. Структурные группы 2-ого класса.

 

Структурная группа второго класса первого вида состоит из двух звеньев и трех вращательных кинематических пар (поэтому ее иногда обозначают ВВВ). Другие виды структурной группы образуются из первого путем замены одной или двух вращательных кинематических пар на поступательные (в обозначениях буквами это выглядит так: ВПВ, ВВП, ВПП, ПВП). Все три вращательные кинематические пары нельзя заменить на три поступательные, так как получится одно звено из трех деталей.

Можно заметить, что определяя степень подвижности структурной группы, мы подразумеваем присоединение внешних кинематических пар к стойке, не обозначая (не рисуя) стойку.

2. n=4, P₁=6. С таким набором звеньев и кинематических пар различают группы третьего (рис. 6а) и четвертого (рис. 6б) класса. Класс группы равен числу внутренних кинематических пар, образующих самый сложный замкнутый контур.

 

Рис.6 Структурные группы третьего (а) и четвертого (б) классов.

 

 

Треугольник 2 на рис. 6а и 1 и3 на рис. 6б считается одним звеном, которое хотя и состоит из трех элементов, но образует жесткую систему. Четырехугольник АВСD на рис. 6б не может образовать жесткую систему и считается состоящим из четырех звеньев.

На рис. 6а самый сложный замкнутый контур-треугольник и поэтому группа 3-его класса. На рис. 6б внутренний контур-четырехугольник и поэтому группа относится к 4-му классу.

 

3. n=6, P₁=9. Здесь можно привести пример структурной группы третьего класса (рис.7),

где самый сложный внутренний замкнутый контур состоит из 3-х кинематических пар.

Рис. 7. Структурная группа третьего класса.

 

Теперь разложим схему механизма рис. 4 на структурные группы. Отделение структурных групп выполняют в таком порядке, чтобы степень подвижности оставшейся цепи не менялась. Поэтому, можно выделить структурную группу 2-ого класса, состоящую из звеньев 4-5 и кинематических пар E,F,H. Далее идет структурная группа 2-ого класса, состоящая из звеньев 2-3 и кинематических пар B,C,D. И остался механизм 1-ого класса звено 1, кинематическая пара А и стойка.

Т.е., в соответствии с правилом Ассура образования плоских механизмов, можно сказать, что к механизму первого класса звено 1 (I₁), последовательно присоединяются две структурные группы второго класса звенья 2-3 (II_2,3) и звенья 4-5 (II_4,5). Принято записывать формулу строения механизма в следующем виде (римскими цифрами обозначают класс механизма и структурных групп)

 

I₁← II_2,3← II_4,5

 

Класс механизма определяется наивысшим классом структурных групп, входящих в механизм. Таким образом схема на рис. 4 относится к механизму II класса.

Определение класса и формулы строения механизма позволяют выбрать рациональный метод кинематического и силового анализа механизма. Например, кинематический анализ начинают с механизма I класса и далее переходят к структурным группам в порядке их присоединения, а силовой анализ начинают с последней структурной группы и затем в соответствии с формулой строения механизма переходят к другим группам, завершая силовой расчет расчетом ведущего звена. По классу механизма выбирают метод кинематического и силового расчета структурных групп соответствующего класса.

В заключении этого раздела заметим, что на структурной схеме механизма обязательно нужно указать ведущее звено, так как от этого зависит и класс, и формула строения механизма, а, следовательно, и порядок кинематического и силового расчета.

 

3. Построение планов скоростей.

Построение планов скоростей так же, как и построение положений механизма, начинают с ведущего звена и далее переходят к структурным группам порядке их присоединения к ведущему звену в соответствии с формулой строения механизма. Построение плана скоростей механизма, например, для его третьего положения (рис. 8) будем выполнять в следующем порядке.

1. Угловая скорость ведущего звена кривошипа

.

2. Окружная скорость точки В^*)

Напомним, что линейная скорость точки направлена по касательной к траектории этой точки. Поэтому, скорость точки В направлена по касательной к окружности радиуса АВ, т.е. перпендикулярно кривошипу в рассматриваемом положении.

Рис. 8. Схема механизма для трёх (из 12) положений кривошипа АВ

 

Для построения плана скоростей (рис. 9) выбираем масштабный коэффициент скорости как отношение модуля скорости точки В к отрезку на плане скоростей ^**, изображающему эту скорость, т.е.

.

Точка p на плане скоростей является полюсом плана скоростей, в котором скорость равна нулю.

3. Определение скорости точки С.

Точка С является внутренней кинематической парой первой присоединенной структурной группы, внешние кинематические пары которой полностью определены. Поэтому скорость точки С как вектор находим из решения системы двух векторных уравнений движения точки С относительно внешних кинематических пар В и D:

(6.1)

Здесь количество черточек под скоростью показывает число известных характеристик скорости. Так скорости точек B и D полностью известны (величина и направление): скорость точки В нашли в предыдущем пункте, а скорость точки D равна нулю, как связанной со стойкой. Относительные скорости точки С относительно точки В v_cb и точки С относительно точки D v_cd известны только по направлению, перпендикулярно соответственно звеньям СВ и CD. Решаем эту систему графически.

Выбираем положение полюса плана скоростей р (рис. 9) и из него перпендикулярно звену АВ в его третьем положении в сторону угловой скорости ω1 проводим вектор длиной (рb), соответствующий скорости точки В (на рис.9 надписи правильные, но по технической причине направления не соответствуют положениям звеньев на рис.8).

 

Рис.9 План скоростей механизма.

 

Далее в соответствии с первым уравнением системы (6.1) через точку b на плане скоростей проводим линию перпендикулярную звену CВ на схеме механизма, что соответствует направлению скорости точки С относительно точки B.

Скорость точки D равна нулю и на плане скоростей она совпадает с полюсом. Поэтому через полюс (точку d) в соответствии со вторым уравнением системы (6.1) проводим линию перпендикулярную звену СD, что соответствует направлению относительной скорости точки С относительно точки D. Точка пересечения направлений относительных скоростей дает положение точки С, а вектор (p с) – скорость точки С – решение системы векторных уравнений (6.1). Численное значение скоростей равно

 

*) На схеме механизма кинематические пары и особые точки обозначают прописными (большими) буквами, а скорость и ускорение этих точек имеют индексы в виде строчных (малых) буквах

**⁾ Отрезок, отмеряемый с плана скорости или ускорения, будем изображать в круглых скобках.

 

Теперь, зная скорости точек, можно найти угловые скорости звеньев. Угловая скорость

первого звена задана. Угловая скорость второго звена (ВС) равна и направлена по часовой стрелке. Это направление определено по скорости точки С относительно точки В. По первому уравнению системы (6.1) вектор (pc) на плане скоростей равен сумме векторов (pb) и (bc), т.е. вектор (bc) направлен от точки b к точке с. Переносим этот вектор в точку С на схеме механизма рис. 9 и видим, что он стремится повернуть звено ВС относительно точки В по часовой стрелке.

Угловая скорость третьего звена (СD) и направлена против часовой стрелки, т.к. скорость точки С относительно точки D направлена вниз (см. план скоростей рис. 9) и стремится повернуть звено (рис. 8) против часовой стрелки.

Скорость любой точки звена СD равна произведению угловой скорости на расстояние этой точки от точки D. Т.е. скорость точки Е можно найти из подобия: точка е на плане скоростей должна делить отрезок (cd) в таком же отношении, как точка Е делит звено CD на схеме механизма и .

Теперь можем перейти к следующей структурной группе, состоящей из звеньев 4 (EF) и 5 (ползун). Здесь достаточно одного векторного уравнения (6.2) движения точки F относительно точки Е, т.к. известно направление движения связанной с ползуном вращательной пары F: параллельно направляющей, т.е. вертикально. Скорость точки Е уже найдена, а скорость точки F относительно точки E известна по направлению: перпендикулярно FE.

(6.2)

Строим это уравнение (рис. 9). Через полюс p, т.к. направляющая ползуна неподвижна, проводим вертикальную линию, а через точку е направление относительной скорости точки F относительно Е перпендикулярно FE. Пересечение этой линии с вертикалью дает решение уравнения (6.2): положение точки f и ее скорость вектор (p f), численно равный

.

Скорость точки F относительно точки Е направлена вправо, т. к. отрезок (p f) равен сумме отрезков (p е) и (еf). Поэтому угловая скорость четвертого звена направлена против часовой стрелки. Т.е., вектор (ef) с плана скоростей прикладываем к точке F на схеме механизма (рис. 9) и смотрим, что относительно точки Е он стремится повернуть звено EF против часовой стрелки. Значение угловой скорости звена ЕF равно

.

Построение плана скоростей завершено.

 

4. Построение планов ускорений.

 

Пример построения плана ускорений выполним тоже для третьего положения механизма. Порядок построения плана ускорений такой же как и при построении плана скоростей: начинаем с ведущего звена и переходим к структурным группам в порядке их присоединения. Векторные уравнения движения аналогичны, но относительное ускорение внутренней кинематической пары структурной группы относительно внешней состоит не из одной, а из двух составляющих: нормальной и тангенциальной. Нормальная составляющая возникает при криволинейной траектории точки, направлена вдоль звена к той точке, относительно которой рассматривается движение, и по величине равна

 

, (11.1)

где v_отн – относительная скорость движения внутренней кинематической пары группы относительно внешней;

– расстояние между кинематическими парами (длина звена);

ω – угловая скорость звена.

Так как план скоростей уже построен, то величину нормальной составляющей мы всегда можем подсчитать.

Тангенциальная составляющая характеризует изменение скорости по величине, направлена перпендикулярно линии, соединяющей рассматриваемые точки (перпендикулярные звену) или вдоль направляющей в случае ползуна и по величине будем находить построением плана ускорений.

1. Ускорение точки В.

По условию скорость кривошипа постоянна. Поэтому на точку В относительно точки А действует только нормальная составляющая

 

По значению этого ускорения выбираем масштаб плана ускорений

 

где q – полюс плана ускорений;

(qb) – отрезок на плане ускорений, который мы выбираем для изображения ускорения точки В.

Выбираем положение полюса q и из него проводим линию параллельную звену АВ и на ней откладываем вектор (qb), направленный влево (от В к А по схеме механизма) рис. 10.

2. Ускорение точки С.

Для внутренней кинематической пары С, аналогично построению плана скоростей, записываем два векторных уравнения движения точки С относительно внешних кинематических пар структурной группы.

(11.2)

Рис. 10. План ускорений механизма.

 

Ускорение внешних кинематических пар известны: а_b нашли в первом пункте, а_d=0,т.к. точка D связана со стойкой. На плане ускорений точка d совпадает с полюсом q.

Нормальное ускорение точки С относительно точки В и точки С относительно точки D тоже полностью известны: они направлены по звену к центру вращения, т.е. к точкам В и D соответственно, а по величине определяются по зависимости (11.1)

 

где скорости v_cb и v_cd определены ранее по плану скоростей.

Тангенциальные ускорения и известны только по направлению: перпендикулярно соответствующему звену.

Строим первое уравнение системы (11.2): из конца вектора (qb) проводим линию параллельную звену СВ на схеме механизма (рис. 8) и на ней откладываем вверх (от С к В по рис. 10) вектор (bn₁) по величине равный

 

,

а через его конец проводим направление тангенциального ускорения перпендикулярно звену СВ. Первое уравнение построено.

Строим второе уравнение системы (11.2): из точки d, т.е. через полюс плана ускорений q, проводим линию параллельно звену CD и на ней вправо (от C к D по рис. 8) откладываем вектор (dn₂), равный по величине

 

а через его конец проводим направление тангенциального ускорения перпендикулярно звену CD. Второе уравнение построено.

Решением системы (11.2) является вектор (qc), точка с которого найдена пересечением направлений тангенциальных составляющих. Численное значение ускорений равно:

 

Направление векторов и определено по направлению уже известных слагаемых, сумма которых равна вектору (qc).

По тангенциальным ускорениям найдем угловые ускорения звеньев:

 

и

Эти ускорения направлены против часовой стрелки, что определено следующим образом: вектор (n₁c) с плана ускорений переносим в точку С на схеме механизма и смотрим направление, в котором этот вектор стремится повернуть звено СВ относительно точки В; аналогично вектор (n₂c) переносим в точку с и определяем направление, в котором этот вектор стремится повернуть звено СD относительно точки D.

3. Ускорение точки Е.

Ускорение любой точки звена CD есть геометрическая сумма нормального и тангенциального ускорений этой точки относительно точки D, а модуль этого ускорения, например, точки Е равен

 

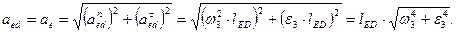
Из этого выражения следует, что, как и при построении плана скоростей рис. 9, положение точки е на плане ускорений можно найти из подобия

 

а ускорение точки Е равно

 

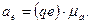
4. Ускорение точки F.

Переходим к определению ускорения внутренней кинематической пары последней структурной группы. Эта кинематическая пара точка F является вращательной, соединенной с ползуном, который способен перемещаться только вдоль направляющей, т.е. вертикально. Поэтому, ускорение точки F может быть направлено тоже только вертикально и остается одна неизвестная – величина этого ускорения, для чего достаточно одного векторного уравнения

 

(11.3)

 

Ускорение точки Е уже известно. Нормальное ускорение точки F относительно точки Е тоже полностью известно: оно направлено параллельно звену FE от точки F к точке Е (к центру относительно вращения) и по величине равно

 

Тангенциальное ускорение точки F относительно точки Е известно только по направлению: перпендикулярно звену FE.

Строим уравнение (11.3). Через полюс q, т.к. направляющая ползуна неподвижна, проводим линию параллельную F^'F^''. Из точки е проводим линию параллельную звену FE и на ней вверх (от F к Е по рис. 8) откладываем отрезок

,

а через его конец проводим линию перпендикулярную звену FE – направление тангенциального ускорения. Пересечение этой линии с линией, параллельной F^'F^'', дает положение точки f, а вектор - решение уравнения (11.3). Ускорение точки F и тангенциальное ускорение точки F относительно точки Е равны

Направление тангенциального ускорения определено по известным слагаемым и , которые вместе с дают суммарный вектор .

Угловое ускорение звена EF равно

.

Оно направлено по часовой стрелке, что найдено путем переноса вектора с плана ускорений в точку F схемы механизма, откуда видно, как вектор стремится повернуть звено FE относительно точки Е по часовой стрелке.

Теперь план ускорений механизма полностью построен. Следует лишь заметить, что если какой-то вектор, например, в масштабе плана ускорений составляет менее 1…2 мм, то его можно не откладывать, считая достаточно малым.

 

5. Контрольные вопросы к защите

Первого листа проекта.

 

1. В чем отличие механизма от машины и назначение механизма?

2. Почему механизм с пятью подвижными звеньями называется шестизвенным?

3. Определение и классификация кинематических пар. Примеры.

4. Как определить число возможных ведущих звеньев кинематической цепи?

5. Признаки структурной группы.

6. Порядок структурного и кинематического анализа механизма.

7. В каких положениях кривошипа механизм занимает крайнее положение?

8. Принцип кинематического расчета структурных групп II класса.

9. Порядок построения планов скоростей и ускорений.

10. Как определить с помощью планов скоростей и ускорений величину и направление угловых скоростей и ускорений звеньев.

 

Литература

Теория механизмов и механика машин; Учеб. для вузов. Под ред. Г.А. Тимофеева

М.: Изд-во МГТУ им. Н.Э.Баумана, 2009.-688 с.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: