 |
Закон Ома в дифференциальной форме
|
|
|
|
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Электрический ток
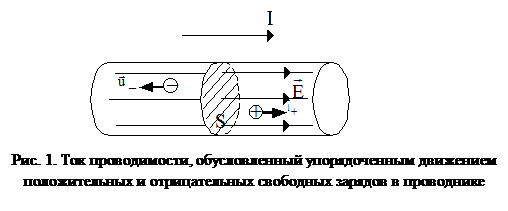
Электрическим током называется упорядоченное (направленное) движение электрических зарядов. При таком движении заряды называются носителями тока. Мы ограничимся лишь рассмотрением тока в проводнике, который называют током проводимости. В проводнике под действием приложенного электрического поля с напряженностью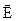 
положительные носители тока перемещаются в направлении поля, а отрицательные – в противоположную сторону (рис. 1). Скорость упорядоченного движения носителей тока при этом будем обозначать буквой 
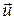. За направление электрического тока принимается направление упорядоченного движения положительных носителей.
 |
Количественной характеристикой электрического тока служит скалярная величина, называемая силой тока I, равная заряду, переносимому носителями через поперечное сечение S проводника в единицу времени:
, (1)
где dq – заряд, переносимый носителями тока через поперечные сечение S проводника за время dt (рис. 1).
Ток, не изменяющийся со временем ни по величине, ни по направлению, называется постоянным. Для постоянного тока
, (2)
где q – заряд, проходящий через поперечное сечение S проводника за время t.
В СИ единица измерения силы тока ампер (А) является основной. На основании (1) через ампер определяется единица заряда – кулон, являющаяся производной единицей:
.
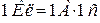Электрический ток может быть распределен неравномерно по поперечному сечению S проводника, по которому он течет. В этом случае детально ток характеризуют с помощью вектора плотности тока 
.
Модуль вектора
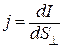, (3)
где dI – сила тока через расположенную в данной точке площадку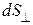 
, перпендикулярную к направлению движения носителей.
|
|
|
Численно плотность тока j равна силе тока через единицу площади поверхности, перпендикулярной к направлению движения носителей. За направление вектора 
принимается направление скорости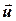 
упорядоченного движения положительных носителей тока.
Плотность тока измеряется в 
.
 |
Поле вектора плотности тока
изображается графически с помощью линий тока, которые строятся так же, как линии напряженности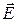 
. На рис. 2 изображены линии тока в проводнике, площадь поперечного сечения S которого плавно увеличивается слева направо. Величина плотности тока при этом уменьшается 
.
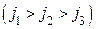Сила тока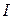 
через произвольную поверхность S находится как поток вектора через нее:
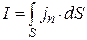, (4)
где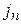 
– проекция вектора на нормаль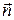 
к поверхности.
Если линии тока перпендикулярны к поперечному сечению S проводника и плотность тока j во всех точках этого сечения одинакова, то выражение (4) принимает простой вид
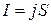. (5)
Закон Ома в дифференциальной форме
Закон Ома является одним из важнейших законов электродинамики. В интегральной форме он был экспериментально открыт для металлических проводников немецким физиком Омом в 1826 г. Представим этот закон в дифференциальной форме исходя из простых модельных представлений.
Рассмотрим металлический проводник, в котором носителями тока являются электроны с зарядом 
и массой m. Проанализируем сначала движение отдельного электрона. Под действием кулоновской силы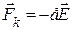 
, действующей со стороны поля с напряженностью 
, электрон движется со скоростью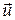 
против вектора (рис. 3).
При своем движении электрон взаимодействует с другими электро-нами и ионами кристаллической решетки. Это взаимодействие обуслов-ливает сопротивление движению электрона. Опыт показывает, что это явление можно учесть, рассматривая движение электрона в среде, в которой на него действует сила сопротивления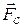 
, пропорциональная скорости :
|
|
|
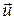, (6)
где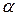 
– коэффициент пропорциональности.
Следовательно, согласно второму закону Ньютона, уравнение движения электрона имеет вид
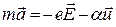. (7)
С увеличением скорости упорядоченного движения электрона сила 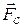быстро растет, что приводит к установлению равновесия между силам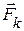и 
и 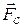. Ускорение электрона становится равным 
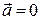, а уравнение (7) принимает вид
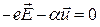. (8)
Из уравнения (8) следует, что между скоростью упорядоченного движения электрона пропорциональна напряженности поля:
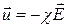, (9)
где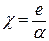 
– коэффициент пропорциональности, называемый подвижностью электрона.
Численно подвижность носителя тока (электрона) равна скорости его упорядоченного движения в электрическом поле с напряженностью, равной единице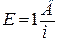 
.
Подвижность носителей тока c измеряется в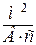 
.
Найдем теперь связь плотности тока со скоростью упорядоченного движения электронов 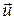. Обозначим через n концентрацию электронов, т.е. число электронов в единице объема металлического проводника. В этом случае через поперечное сечение проводника S (рис. 1) за время dt переносится заряд dq, заключенный в объеме 
:
.
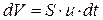Отсюда получаются выражения для силы тока
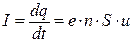
и для плотности тока
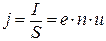. (10)
Переписав (10) в векторном виде, получим искомую связь плотности тока со скоростью упорядоченного движения электронов:
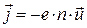. (11)
Подставив (9) в (11), установим связь плотности тока с напряженностью поля в металлическом проводнике:
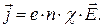(12)
Коэффициент пропорциональности между и 
в формуле (12) называется удельной электрической проводимостью s металла и определяется его свойствами:
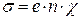. (13)
Удельная электропроводность измеряется в сименсах на метр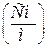 
.
Таким образом, выражение (12) с учетом (13) можно записать так:
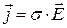. (14)
Формула (14) выражает закон Ома в дифференциальной (локальной) форме: плотность тока в произвольной точке проводника пропорциональна напряженности 
поля в этой точке. Так как закон сформулирован для точки, а не для участка проводника, то он называется локальным или дифференциальным, хотя никаких дифференциалов или производных не содержит. Закон Ома справедлив не только для металлов, но и для некоторых других изотропных проводников.
|
|
|
