Разработка полосового фильтра Баттерворта

Анализ задания

 

В данном разделе произведен расчет ПФ, предназначенного для аппаратуры уплотнения специального типа.

Рассчитанный фильтр должен удовлетворять следующим требованиям:

- затухание фильтра в полосе пропускания не должно превышать заданной неравномерности затухания Dа;

- в полосе задержания затухание должно быть не меньше гарантированного затухания а₀.

Неравномерность затухания и гарантированное затухание определяют количество элементов, число звеньев схемы, причем данные величины должны быть обеспечены при любых обстоятельствах.

Требования к частотной зависимости затухания ПФ Баттерворта:

- Границы полосы пропускания фильтра: ¦_-х = 31 кГц, ¦_х = 42 кГц;

- Границы полосы задержания фильтра: ¦_-к = 28,1 кГц, =44,9 кГц

- Неравномерность характеристики затухания в ПП: Dа=1,55 дБ;

- Гарантированное затухание в полосе задержки: а_о = 19,575 дБ;

- Сопротивление генератора и нагрузки: R_г = R_н = 350 Ом.

Требования к частотной зависимости затухания этого фильтра изображены на рисунке 2.1:

Расчет ПФ Чебышева

 

Расчет ПФ Баттерворта производится на основе расчета ФНЧ-прототипа, для которого производится пересчет частот, при этом порядок расчета следующий:

1)  пересчет требований, сформулированных к ПФ, в требования к ФНЧ-прототипу;

2)  расчет ФНЧ-прототипа;

 

Рис 2.1. Требования к характеристике затухания полосового фильтра

 

3) пересчет параметров элементов ФНЧ-прототипа в параметры ПФ;

4) выбирается схема фильтра и определяется число элементов в ней;

5) изображается схема фильтра с параметрами элементов по ГОСТ и производится контрольный расчет затухания фильтра.

Полосовые фильтры, полученные реоктансным преобразованием частоты, обладают геометрически симметричными характеристиками затухания.

Требования же, предъявляемые к реальному фильтру, могут не обладать указанной симметрией. Частоты ¦_-Х , ¦_Х, ¦_-К считаем фиксированными, тогда

 и .

Требования к фильтру удовлетворяют геометрической симметрии, а именно:

.

Найдем граничные частоты полосы пропускания и полосы задерживания ФНЧ-прототипа:

;

.

По найденным граничным частотам ¦_0П и ¦_КП, а также заданным Dа и а₀ рас­считаем ФНЧ с характеристиками затухания Баттерворта.

Минимально возможный порядок передаточной функции рассчитывается по формуле с учетом нормированной частоты полосы задержания ФНЧ-прототипа: 

;

         (5)

Подставив в (5) численные значения рассчитаем порядок фильтра:

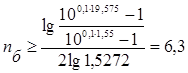
Таким образом, для реализации фильтра необходимо принять большее целое число, т.е. принимаем n_б=7.

Выберем схему ФНЧ-прототипа, которая определяется на основании принятого значения n. Она будет иметь вид, показанный на рисунке 2.2.

Из [1] по таблице, относящейся к фильтрам нижних частот Баттерворта необходимо выписать нормированные значения емкостей и индуктивностей в зависимости от Dа, а₀ и ¦_КП. Эти значения выбираем для меньшего значения Dа=1,55 дБ: L₁ = 0,445; L₃ = 1,802; L₅ =1,802; L₇ = 0,445; C₂ = 1,247; C₄ = 2,000; C₆ =1,247

 

Рис. 2.2 Схема ФНЧ - прототипа для расчёта

 

Для получения истинных значений параметров L и C фильтра необходимо определить коэффициенты денормирования K_L и K_C, причем, в данном случае пересчета частоты выполнять не нужно.

Коэффициент денормирования для индуктивности равен:

.

Коэффициент денормирования для емкости равен:

.

Зная коэффициенты денормирования, рассчитаем истинные значения индук­тивностей и емкостей по формулам:

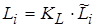 и         (6)

Подставив численные значения в (6) получим:

,

,

,

,

,

,

 

 

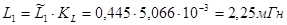Рассчитаем затухание фильтра по формуле:  для различных нормированных значений частоты, включая обязательно граничные частоты полос пропускания и задержания фильтра:

а)

б)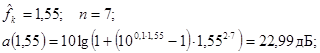

в)

Перейдем к схеме ПФ Баттерворта. Для этого каждую индуктивность ФНЧ-прототипа заменяем последовательным соединением этой же индуктивности и емкости C'_i, значение которой выбирается из условия резонанса между ними на частоте ¦₀. Каждая емкость ФНЧ-прототипа заменяется параллельным конту­ром, состоящим из этой же емкости и индуктивности L'_i, обеспечивающий ре­зонанс на частоте ¦₀, т. е:

, .

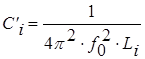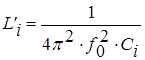Параллельно с емкостями С₂, С₄, и С₆  включаются соответственно следующие индуктивности:

;

;

Последовательно с индуктивностями L₁, L₃, L₅ и L₇ включаются соответствующие емкости:

;

;

.

Таким образом, схема полосового фильтра Баттерворта будет иметь вид, представленный на рисунке 2.3.

 

Рис. 2.3. Схема рассчитанного полосового фильтра

 

Представим характеристику затухания рассчитанного полосового фильтра Баттерворта (рис. 2.4).

Так как рассчитанные емкости конденсатора отличаются от ГОСТа, подбором номиналов конденсаторов получим нужную величину емкости конденсаторов:

С’₁ = 8200 пФ

С₂ = 2000 пФ

С’₃ = 2000 пФ

С₄ = 82000 пФ

С’₅ = 2000 пФ

С₆ = 47000 пФ

С’₇ = 8200 пФ

 

Рис. 2.5 Характеристика затухания рассчитанного полосового фильтра

 

Тип конденсатора необходимо выбирать с учётом частоты, на которой он будет работать, напряжения, под которыми он будет находиться, а также исходить из массогаборитных и стоимостных показателей. В данном случае целесообразно использовать конденсаторы типов

Катушки индуктивности производятся на заводе-изготовителе по рассчитанным параметрам и их пересчёта не требуется.

Таким образом, полосовой фильтр Баттерворта полностью рассчитан, и его принципиальная схема представлена в приложении 2.1, а спецификация элементов - в приложении 2.2.

Для проверки правильности проведенных расчетов проведем моделирование фильтра в среде Еlektronics Workbench, версия 5.12. Полученная в результате характеристика затухания фильтра приведена на рисунке 2.5

Рис. 2.5 Характеристика затухания рассчитанного полосового фильтра

 

Данный фильтр применяется для выделения или подавления определенных колебаний, разделения каналов, формирования спектра сигналов. Фильтр входит в состав многоканальных и радиорелейных систем передачи, измерительной аппаратуры, в каскады радиопередатчиков и радиоприемников.

3 2,625

Заключение

 

В результате выполнения курсовой работы были рассчитаны фильтр высоких частот Чебышева пятого порядка и полосовой фильтр Баттерворта седьмого порядка. Характеристики затуханий, построенные по рассчитанным частотам отвечают требованиям к полосам задержания и пропускания. Проведенное моделирование показало, что характеристики рассчитанных фильтров близки к идеальным, что подтверждает точность расчёта.

Библиографический список

 

1. Богданов Н.Г. Расчёт электрических фильтров. – Пособие по курсовому и дипломному проектированию.- Орел: ВИПС, 2000г.

2. Зааль Р., Справочник по расчетам фильтров. - М.: Радио и связь, 1983

Приложение 1.2

 

Позиционное обозначение	Наименование элементов	Номинал	Кол-во
Конденсаторы
С11,С51	К21-9-М150-4700 ± 5%	4700 пФ	2
С12,С52	К21-9-М150-82 ± 5%	82 пФ	2
С13,С53	КД-1а-М75-7,5 ± 5%	7,5 пФ	2
С21	К21-9-М150-2700 ± 5%	2700 пФ	1
С22	К21-9-М150-68 ± 5%	68 пФ	1
С23	КД-1а-М75-2 ± 5%	2 пФ	1
Катушки индуктивности
L2,L4	Катушка	489 мкГн	2

 

 

Приложение 2.2

 

Позиционное обозначение		Наименование, тип		Номинал		Кол-во
Конденсаторы
С’1		К21-9-М750-8200 ± 5%		8200 пФ		1
С2		К21-9-М750-47000 ± 5%		47000 пФ		1
С’3		К21-9-М750-2000 ± 5%		2000 пФ		1
С4		К21-9-М750-82000 ± 5%		82000 пФ		1
С’5		К21-9-М750-2000 ± 5%		2000 пФ		1
С6		К21-9-М750-47000 ± 5%		47000 пФ		1
С’7	К21-9-М750-8200 ± 5%		8200 пФ		1
Катушки индуктивности
L1		Катушка		2,25 мГн		1
L’2		Катушка		0,38 мГн		1
L3		Катушка		9,13 мГн		1
L’4		Катушка		0,23 мГн		1
L5		Катушка		9,13 мГн		1
L’6		Катушка		0,38 мГн		1

 

12	Поделиться:

Воспользуйтесь поиском по сайту: