 |
Критические границы и допустимые изменения ресурса
|
|
|
|
Рассмотрим пример:
Для производства двух видов изделий А и В используется четыре различных вида сырья. Каждый из видов сырья может быть использован в количестве, соответственно не большем 18, 16, 5 и 21 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции каждого вида приведены в таблице.
| Вид сырья | Нормы затрат сырья (кг) на единицу продукции | |
| А | В | |
| I II III IV | ||
| Цена единицы продукции (руб.) |
Определить план выпуска продукции, при котором обеспечивается ее максимальная стоимость, и провести анализ чувствительности.
ЭММ (решали задачу симплекс-методом):
F = 2x1 + 3х2 à max при ограничениях:
х1 + 3х2 <= 18
2х1 + х2 <= 16
х2 <= 5
3x1 <= 21
х1, х2 >= 0
симплекс-методом получили на последнем шаге:
F= 24 – 4/5х3 – 3/5х4 при оптимальном БР Х* =(6; 4; 0; 0; 1; 3).
| Базис | Свободный член | Переменные | Оценочное отношение | |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | |||
| Х1 | -1/5 | 3/5 | ||||||
| Х5 | -2/5 | 1/5 | ||||||
| Х2 | 2/5 | -1/5 | ||||||
| Х6 | 3/5 | -9/5 | ||||||
| F | 4/5 | 3/5 |
В этом примере связанными являются ограничения по I и II видам сырья. Эти два вида сырья используются полностью. Остальные - избыточны (остаток по III виду сырья – 1 кг, по IV – 3 кг.
Есть смысл докупать только сырье I вида, если рыночная цена на него ниже 0,8 руб. за единицу (т.к. прирост целевой функции будет равен 0,8 руб.), и сырье II вида, если рыночная цена на него ниже 0,6 руб. за единицу (т.к. прирост целевой функции будет равен 0,6 руб.).
Важно определить до скольких единиц имеет смысл закупать первые два вида сырья.
Предположим, что запасы I вида сырья изменились на Δb1. Тогда затраты на ресурсы в соответствии с целевой функцией ДЗ будут равны:
|
|
|
Z =(18+ Δb1) y1 + 16y2 +5y3 + 21y4.
| Базис | Свободный член | Переменные | Оценочное отношение | |||||
| Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | |||
| Y1 | 4/5 | 2/5 | -3/5 | 1/5 | -2/5 | |||
| Y2 | 3/5 | -1/5 | 9/5 | -3/5 | 1/5 | |||
| Z |
Заменяем переменные у1 и у2 их выражениями через неосновные переменные оптимального БР:
у1= 4/5 – 2/5 у3 + 3/5 у4 – 1/5 у5 + 2/5 у6
у2= 3/5 + 1/5 у3 – 9/5 у4 + 3/5 у5 – 1/5 у6,
подставляем в целевую функцию:
Z =(18+ Δb1) (4/5 – 2/5 у3 + 3/5 у4 – 1/5 у5 + 2/5 у6) + 16 (3/5 + 1/5 у3 – 9/5 у4 + 3/5 у5 – 1/5 у6) +5y3 + 21y4 =
= (24 + 4/5 Δb1) + (1 – 2/5 Δb1) у3 + (3 + 3/5 Δb1) у4 + (6 – 1/5 Δb1) у5 + (4 + 2/5 Δb1) у6.
|
Y* =(4/5; 3/5; 0; 0; 0; 0),
достаточно, чтобы коэффициенты при неосновных переменных в последнем выражении оставались неотрицательными, т.е.
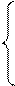 1 – 2/5 Δb1 >= 0
3 + 3/5 Δb1 >= 0
6 – 1/5 Δb1 >= 0
4 + 2/5 Δb1 >= 0
| и | Δb1 <= 2,5 Δb1 >= -5 Δb1 <= 30 Δb1 >= -10 |
Откуда:
–5 <= Δb1 <= 2,5
18 -5 <= b1 + Δb1 <= 18 + 2,5 или 13 <= b1 + Δb1 <= 20,5,
т.е. при неизменности теневых цен (или оценок ресурсов) запас I вида сырья может изменяться в пределах от 13 до 20,5 единиц.
Аналогично можно высчитать пределы изменения по запасам II вида сырья, который может меняться от 11 до 17, 67 единиц.
Можно определить графическим способом.
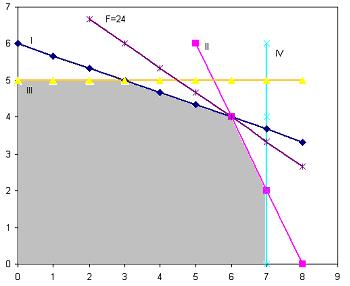
Посмотрим на график, который строили при решении задачи графическим способом.
|
|
|
|
|
|
|
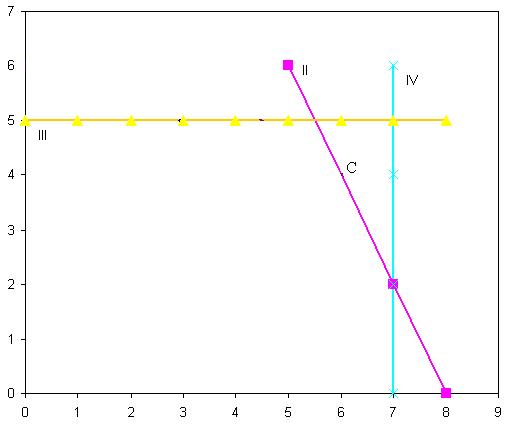
Если в нашем примере постепенно увеличивать запас I вида сырья, то оптимальный план будет смещаться, оставаясь на пересечении границ по I и II видам сырья. Так будет продолжаться до тех пор, пока он не дойдет до точки Е – точки пересечения границ по II и III видам сырья. В точке Е пересекутся три границы: по I, II и III видам сырья.
Этот момент является критическим. Дальнейшее увеличение запаса I вида сырья приведет к избыточности данного ресурса. Он станет несвязанным, его теневая цена будет равна 0. Связанным станет III вид сырья. Таким образом, в наборе связанных ресурсов, после прохождения критического положения границы, один ресурс будет заменен другим, два этих ресурса изменят свой статус.
|
|
|
Расчет критической границы по I виду сырья можно провести следующим образом. Сначала определим координаты точки пересечения границ по II и III видам сырья. Для этого следует решить соответствующую систему уравнений
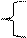2х1 + х2 = 16
х2 = 5
В результате получим:
x1 = 5,5 x2 = 5.
Подставим эти значения в левую часть неравенства, определяющего ограничение по I виду сырья:
х1 + 3х2 = 5,5 + 3´5 = 20,5.
Полученная величина 20,5 и является верхней критической границей по I ресурсу. Таким образом, исходный объем I вида сырья, равный 18 кг, можно увеличить на 2,5 кг без изменения статуса ограничений и без изменения теневой цены ресурса. Величина 2,5 кг в этом примере является допустимым увеличением этого вида сырья.
Нижняя критическая граница и, соответственно, допустимое уменьшение вычисляются аналогично. В нашем примере при уменьшении объема I вида сырья оптимальный план будет смещаться налево-вниз. Критическим будет такая величина объема ресурса, при которой линия I вида сырья пройдет через точку пересечения F границ по II и IV видам сырья.
При дальнейшем уменьшении доступного объема I вида сырья произойдет изменение статуса некоторых ограничений. Именно, связанными ресурсами станут I и IV виды сырья, а II вид сырья станет несвязанным, и его теневая цена будет равна 0.
Для вычисления координат точки F решим соответствующую систему уравнений:
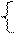2х1 + х2 = 16
3x1 = 21
В результате получим
x1 = 7 x2 = 2.
Подставим эти значения в левую часть неравенства, определяющего ограничение по I виду сырья:
х1 + 3х2 = 7 + 3´2 = 13.
Величина 13 есть нижняя критическая граница ресурса. Допустимое уменьшение данного ресурса определяется разностью 18 – 13 = 5.
Таким образом, при изменении доступного объема I вида сырья теневые цены и статус ресурсов сохраняются, если его объем остается между вычисленными критическими границами. При переходе через одну из границ, происходит изменение статуса и теневых цен ресурсов.
|
|
|
Аналогично могут быть определены критические границы по остальным ограничениям. Для избыточных ресурсов (их теневая цена равна 0) верхней границы не существует, такой ресурс при любом увеличении объема остается избыточным.
Напомним, что координатные оси являются граничными прямыми ограничений x1 ³ 0, x2 ³ 0. Таким образом, в некоторых ситуациях прохождение через критическую границу может привести к тому, что производство одного из продуктов прекратится (оптимальное значение одной из переменных x1, x2 станет равным 0), или возобновится (оптимальное значение одной из переменных x1, x2 станет больше 0).
Критические границы ресурсов соответствуют границам устойчивости статуса ограничений при изменении их правых частей.
Если запасы первых двух видов сырья будут меняться одновременно, то исследование теневых цен (оценок) усложняется.
Ценовой анализ
Изменение оптимального плана может быть связано с изменением цен на продукцию (коэффициентов при переменных в целевой функции). В рассматриваемой модели цены считаются неизменными. При небольших изменениях цен оптимальный план обычно сохраняет свою оптимальность. При существенных изменениях цен оптимальным становится другой план. Важно разобраться в этом, рассчитать критические ценовые границы. Такое изучение воздействия ценовых изменений на оптимальный план и оптимум относят к ценовому постоптимизационному анализу.
Обратимся к нашему примеру. Цена изделия А составляет 3 руб. за ед. Предположим, что отпускная цена изменилась, и теперь изделие А продается по другой цене. Следует ожидать, что при этом изменится выручка от продаж. Однако изменится ли оптимальный план?
Предположим, что цена Изделия А изменились на Δс1. Тогда прибыль в соответствии с целевой функцией будет равна:
| Базис | Свободный член | Переменные | Оценочное отношение | |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | |||
| Х1 | -1/5 | 3/5 | ||||||
| Х5 | -2/5 | 1/5 | ||||||
| Х2 | 2/5 | -1/5 | ||||||
| Х6 | 3/5 | -9/5 | ||||||
| F | 4/5 | 3/5 |
|
|
|
F =(2+ Δc1) х1 + 3х2.
Заменяем переменные х1 и х2 их выражениями через неосновные переменные оптимального БР:
х1= 6 + 1/5 х3 - 3/5 х4
х2= 4 - 2/5 х3 + 1/5 х4,
подставляем в целевую функцию F и после преобразования получаем:
F =(24 + 6 Δc1) – (4/5 – 1/5 Δc1) х3 – (3/5 + 3/5 Δc1) х4.
Для того, чтобы сохранилось оптимальное решение Х* =(6; 4; 0; 0; 1; 3),
достаточно, чтобы коэффициенты при неосновных переменных в последнем выражении оставались неотрицательными, т.е.
| 4/5 – 1/5 Δc1>= 0 3/5 + 3/5 Δc1>= 0 | и | Δс1 <= 4 Δс1 >= -1 |
Откуда:
–1 <= Δс1 <= 4
2 - 1 <= с1 + Δс1 <= 2 + 4 или 1 <= с1 + Δс1 <= 6,
т.е. оптимальное решение будет неизменно при изменении цен на Изделие А в пределах от 1 до 6 рублей.
Можно определить графическим способом.
|
|
Небольшое изменение цены приведет к незначительному повороту градиента (вместе со всей системой перпендикулярных ему линий уровня целевой функции). В результате оптимальный план останется в прежней точке. При более значительном изменении цены он перейдет в другую вершину области допустимых планов.
Рассмотрим этот вопрос подробнее. Предположим, что цена Изделия А увеличивается. Это соответствует повороту наклона прямой целевой функции по часовой стрелке. При небольшом повороте оптимальный план остается в первоначальной точке C. При достаточно большом повороте оптимальный план перейдет в точку D, находящуюся на пересечении границ по II и IV видам сырья.
Критическая величина цены, при которой происходит переход оптимального плана из одной точки в другую, соответствует положению, когда линия уровня целевой функции параллельна прямой, которой принадлежит отрезок СD. Условием параллельности прямых является пропорциональность коэффициентов при переменных в двух уравнениях: линии уровня целевой функции и границы по II виду сырья. Составим пропорцию с неизвестной ценой c1 изделия А:
F = 2x1 + 3х2
2х1 + х2 <= 16
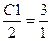
Отсюда получаем c1= 6. Таким образом, при увеличении цены Изделия А с первоначальных 2 до 6 руб. за ед. (и при сохранении цены Изделия В) оптимальный план остается неизменным, по-прежнему следует производить 6 ед. Изделия А и 4 ед. Изделия В. Если же цена поднимется выше 6 руб., то оптимальным планом станет точка D, находящаяся на пересечении границ по II и IV видам сырья. Ее координаты можно определить решением системы соответствующих уравнений.
При цене Изделия А, в точности равной 6 руб., оптимальным является как первоначальный план С, так и новый план D, а также и все точки, лежащие на отрезке СD. В этом случае задача имеет бесконечно много оптимальных планов. Разумеется, все эти разные планы производства обеспечивают в точности одну и ту же величину выручки от продаж.
|
|
|
Верхняя критическая граница цены Изделия А равна 6. Отсюда следует, что допустимое увеличение первоначальной цены равно 4.
Аналогичным образом рассчитывается нижняя граница цены Изделия А, и верхняя и нижняя критические границы цен Изделия В.
Критические границы цен соответствуют границам устойчивости оптимального плана при изменении коэффициентов целевой функции.
|
|
|
