 |
Проверка однородности информации об износах
|
|
|
|
Определение коэффициентов годности и восстановления деталей
Определение технических требований к анализируемой поверхности
Проведём выкопировку эскиза указанной детали и сформируем технические требования на дефектацию заданной поверхности 6 см. [3].
Таблица 1 - Технические требования на дефектацию
| Наименование детали | Контролируемая поверхность | Размер детали | ||
| Корпус коробки передач трактора МТЗ-82 | Поверхность отверстия под стакан ведущей шестерни 2-й ступени редуктора | по чертежу | допустимый в сопряжении | |
| 138 +0,040 | с деталями бывшими в эксплуатации | с новыми деталями | ||
| 138,07 | 138,09 | |||
Эскиз указанной детали приведен в приложении А.
Определение износов деталей и составление вариационного ряда
Значения размеров изношенных деталей (для отверстия – по возрастанию значений размеров) приведены в таблице 2.
Таблица 2 – Размеры изношенных деталей, мм
| 138,062 | 138,073 | 138,076 | 138,080 | 138,084 | 138,089 | 138,094 | 138,101 | 138,109 | 138,114 |
| 138,062 | 138,073 | 138,078 | 138,081 | 138,085 | 138,089 | 138,094 | 138,101 | 138,109 | 138,116 |
| 138,064 | 138,073 | 138,078 | 138,081 | 138,085 | 138,090 | 138,094 | 138,102 | 138,110 | 138,116 |
| 138,066 | 138,073 | 138,079 | 138,082 | 138,086 | 138,090 | 138,097 | 138,103 | 138,110 | 138,118 |
| 138,068 | 138,074 | 138,079 | 138,082 | 138,086 | 138,091 | 138,097 | 138,104 | 138,110 | 138,118 |
| 138,069 | 138,074 | 138,079 | 138,082 | 138,087 | 138,091 | 138,098 | 138,104 | 138,110 | 138,121 |
| 138,070 | 138,075 | 138,079 | 138,082 | 138,087 | 138,091 | 138,099 | 138,105 | 138,110 | 138,122 |
| 138,071 | 138,075 | 138,079 | 138,083 | 138,088 | 138,092 | 138,099 | 138,106 | 138,111 | 138,126 |
| 138,073 | 138,075 | 138,079 | 138,083 | 138,088 | 138,092 | 138,100 | 138,107 | 138,113 | 138,126 |
| 138,073 | 138,076 | 138,080 | 138,083 | 138,089 | 138,093 | 138,100 | 138,107 | 138,113 | 138,126 |
Вычислим износы деталей и составим их вариационный ряд в виде таблицы 3.
Износ i -го отверстия определяют по зависимости
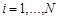; (1)
где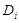 
–диаметр i-го изношенного отверстия;
|
|
|
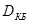– наибольший конструктивный размер отверстия;
N – число анализируемых деталей.
Пример расчета: износ 1-го отверстия:
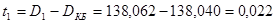мм.
Таблица 3 – Значения износов деталей (вариационный ряд)
| Номер детали | Значение износа детали, мм | Номер детали | Значение износа детали, мм | Номер детали | Значение износа детали, мм | Номер детали | Значение износа детали, мм |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0,022 | 26 | 0,039 | 51 | 0,049 | 76 | 0,064 |
| 2 | 0,022 | 27 | 0,039 | 52 | 0,049 | 77 | 0,065 |
| 3 | 0,024 | 28 | 0,039 | 53 | 0,050 | 78 | 0,066 |
| 4 | 0,026 | 29 | 0,039 | 54 | 0,050 | 79 | 0,067 |
| 5 | 0,028 | 30 | 0,040 | 55 | 0,051 | 80 | 0,067 |
| 6 | 0,029 | 31 | 0,040 | 56 | 0,051 | 81 | 0,069 |
| 7 | 0,030 | 32 | 0,041 | 57 | 0,051 | 82 | 0,069 |
| 8 | 0,031 | 33 | 0,041 | 58 | 0,052 | 83 | 0,070 |
| 9 | 0,033 | 34 | 0,042 | 59 | 0,052 | 84 | 0,070 |
| 10 | 0,033 | 35 | 0,042 | 60 | 0,053 | 85 | 0,070 |
| 11 | 0,033 | 36 | 0,042 | 61 | 0,054 | 86 | 0,070 |
| 12 | 0,033 | 37 | 0,042 | 62 | 0,054 | 87 | 0,070 |
| 13 | 0,033 | 38 | 0,043 | 63 | 0,054 | 88 | 0,071 |
| 14 | 0,033 | 39 | 0,043 | 64 | 0,057 | 89 | 0,073 |
| 15 | 0,034 | 40 | 0,043 | 65 | 0,057 | 90 | 0,073 |
| 16 | 0,034 | 41 | 0,044 | 66 | 0,058 | 91 | 0,074 |
| 17 | 0,035 | 42 | 0,045 | 67 | 0,059 | 92 | 0,076 |
| 18 | 0,035 | 43 | 0,045 | 68 | 0,059 | 93 | 0,076 |
| 19 | 0,035 | 44 | 0,046 | 69 | 0,060 | 94 | 0,078 |
| 20 | 0,036 | 45 | 0,046 | 70 | 0,060 | 95 | 0,078 |
| 21 | 0,036 | 46 | 0,047 | 71 | 0,061 | 96 | 0,081 |
| 22 | 0,038 | 47 | 0,047 | 72 | 0,061 | 97 | 0,082 |
| 23 | 0,038 | 48 | 0,048 | 73 | 0,062 | 98 | 0,086 |
| 24 | 0,039 | 49 | 0,048 | 74 | 0,063 | 99 | 0,086 |
| 25 | 0,039 | 50 | 0,049 | 75 | 0,064 | 100 | 0,086 |
Составление статистического ряда износов
Число интервалов n определяют по зависимости:
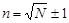(2)
с последующим округлением полученного результата до целого числа
= 
.
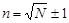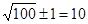Длину интервалов 
вычисляют по зависимости:
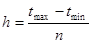, (3)
где 
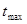и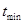 
– наибольшее и наименьшее значения СВ из вариационного ряда соответственно.
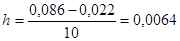мм.
Начало t н i и конец t к i i -го интервала вычисляют по следующим зависимостям:
t н1= t min; t н i = t к(i –1); t к i = t н i + h (4)
Пример решения:
t н1= t min=0,022 мм;
t к 1 = t н 1 + h =0,022+0,0064=0,0284 мм.
Количество наблюдений (значений СВ)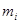 
в i -м интервале (i = 1, …, n) называется опытной частотой. Опытная частота 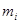, отнесенная к общему числу наблюдений (объему выборки) 
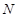, называется опытной вероятностью..
|
|
|
Ее значение определяется по зависимости:
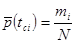, (5)
где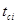 
– значение СВ в середине i -го интервала.
Пример решения:
.
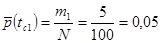Накопленная опытная вероятность, являющаяся статистическим аналогом функции распределения, вычисляется по зависимости:
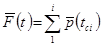(6)
Пример решения:
.
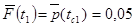Таким образом, статистическим рядом распределения является таблица 4, в которой указаны границы и середины интервалов, опытные частоты, опытные и накопленные опытные вероятности.
Таблица 4 – Статистический ряд распределения износов
| Границы интервала, мм | 0,0220 ... 0,0284 | 0,0284 ... 0,0348 | 0,0348 ... 0,0412 | 0,0412 ... 0,0476 | 0,0476 ... 0,0540 | 0,0540 ... 0,0604 | 0,0604 ... 0,0668 | 0,0668 ... 0,0732 | 0,0732 ... 0,0796 | 0,0796 … 0,0860 |
| Середина интервала, мм | 0,025 | 0,031 | 0,038 | 0,044 | 0,050 | 0,057 | 0,063 | 0,070 | 0,076 | 0,082 |
Опытная частота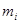 
| 5 | 11 | 17 | 14 | 15,5 | 7,5 | 8 | 12 | 5 | 5 |
| Границы интервала, мм | 0,0220 ... 0,0284 | 0,0284 ... 0,0348 | 0,0348 ... 0,0412 | 0,0412 ... 0,0476 | 0,0476 ... 0,0540 | 0,0540 ... 0,0604 | 0,0604 ... 0,0668 | 0,0668 ... 0,0732 | 0,0732 ... 0,0796 | 0,0796 … 0,0860 |
Опытная вероятность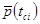 
| 0,05 | 0,11 | 0,17 | 0,14 | 0,155 | 0,075 | 0,08 | 0,12 | 0,05 | 0,05 |
Накопленная опытная вероятность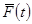 
| 0,05 | 0,16 | 0,33 | 0,47 | 0,625 | 0,7 | 0,78 | 0,9 | 0,95 | 1 |
Определение числовых характеристик статистической совокупности износов
Наиболее применяемыми числовыми характеристиками совокупности значений случайной величины являются:
– среднее значение, характеризующее центр группирования случайной величины;
– среднеквадратическое отклонение и коэффициент вариации, являющиеся характеристиками рассеивания случайной величины.
Так как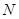 
> 25, то характеристики вычисляются по зависимостям:
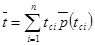, (7)
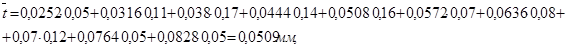
, (8)
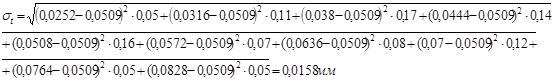
Анализ зависимостей для определения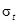 
показывает, что его значение зависит не только от величины рассеивания, но и от абсолютных значений СВ. От этого недостатка свободен коэффициент вариации 
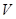, определяемый по зависимости:
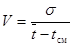(9)
где при N > 25 t см= t н1 –0,5 h;
t см= t н1 –0,5 h =0,022 - 0,5∙0,0064= 0,0188 мм.
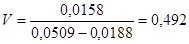
Проверка однородности информации об износах
Проверку на выпадающие точки проводят по критерию Ирвина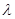 
, который вычисляют по зависимости:
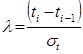, (10)
где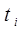 
и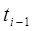 
– смежные значения случайной величины вариационного ряда.
Проверку начинают с крайних значений случайной величины. Вычисленное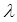 
сравнивают с табличным значением 
, 
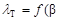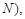взятом из табл. В.1 [1], при доверительной вероятности 
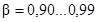и числе наблюдений 
.
|
|
|
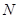При 
переходят к проверке однородности следующего значения СВ. При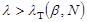 
проверяемое значение СВ признают выпадающим (экстремальным), и оно исключается из выборочной совокупности наблюдений.
Пример решения:
.
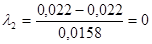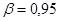при N=100, значение критерия Ирвина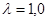 
Вычисленные значения критерия Ирвина запишем в таблицу 5.
Таблица 5 – Значения критерия Ирвина
| - | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0,063 | 0,126 | 0,063 |
| 0 | 0 | 0,126 | 0,063 | 0,063 | 0 | 0 | 0 | 0 | 0,126 |
| 0,126 | 0 | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0,063 | 0 |
| 0,126 | 0 | 0,063 | 0,063 | 0,063 | 0 | 0,189 | 0,063 | 0 | 0,126 |
| 0,126 | 0,063 | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0 | 0 |
| 0,063 | 0 | 0 | 0 | 0,063 | 0 | 0,063 | 0 | 0 | 0,189 |
| 0,063 | 0,063 | 0 | 0 | 0 | 0 | 0,063 | 0,063 | 0 | 0,063 |
| 0,063 | 0 | 0 | 0,063 | 0,063 | 0,063 | 0 | 0,063 | 0,063 | 0,253 |
| 0,126 | 0 | 0 | 0 | 0 | 0 | 0,063 | 0,063 | 0,126 | 0 |
| 0 | 0,063 | 0,063 | 0 | 0,063 | 0,063 | 0 | 0 | 0 | 0 |
Вычисленные значения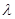 
сравним с табличным значением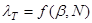 
Взятом из таблицы В.1 [1] при доверительной вероятности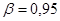 
и числе наблюдений N=100
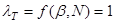
Отсюда следует, что все точки однородны.
|
|
|
12 |
