 |
Определение фактической длины намотки
|
|
|
|
При сплошной намотке фактическая геометрическая длина катушки определяется формулой
(3.12)
числено фактическая длина будет равна
(3.13)
(
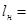
=3,12мм)
По известному числу витков, определили фактическую индуктивность катушки по формуле
, (3.14)
учитывая значение, полученное из выражения (3.13), по графику зависимости 
от 
[1] получили 
, подставляя полученное значение получили
(3.15)
Полученное значение 
на 0,285% отличается от требуемого значения 
, следовательно, коррекцию количества витков можно не выполнять, т. к. полученное значение вполне допустимо.
Расчет оптимального диаметра провода
Расчет оптимального диаметра провода производится графоаналитическим методом:
Определяем по формуле (3.16)
(3.16)
где 
средняя частота рабочего диапазона, Гц;
Вспомогательный коэффициент равен:
Пользуясь графиком (из источника [1], приложение А) определяем поправочный коэффициент 
. Для 
Находим вспомогательный параметр y по формуле (3.17)
(3.17)
где N – число витков обмотки;
k – поправочный коэффициент;
z¢– вспомогательный коэффициент;
D – диаметр каркаса, см.
Вспомогательный параметр y равен:
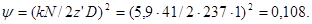(3.18)
при 
<0,3
Определяем величину zопт, по формуле:
zопт=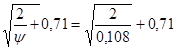 
=5,01 (3.19)
По найденному значению zопт находим оптимальный диаметр провода, по формуле:
(3.20)
Итак, оптимальный диаметр провода будет равен:
Ближайшим по значению диаметра (из выбранного типа) из стандартного ряда является: 
свой выбор остановим на проводе типа ПЭВ- 0,05 ГОСТ 16186 - 74.
Уточнение электрических параметров конструкции
Как, впрочем, и другие конструкции данная конструкция катушки индуктивности не совершенна из-за присутствующих сопротивлений потерь. Сопротивление потерь намотки характеризуется активным сопротивлением провода и его сопротивлением току высокой частоты. Сопротивление провода является физический характеристикой материала, из которого изготовлен данный провод, и является справочной величиной. Активное сопротивление металлического отрезка провода длиной 
и площадью поперечного сечения 
определяется по следующему соотношению
|
|
|
, (3.21)
где 
- удельное сопротивление материала, из которого изготовлен провод, для меди оно составляет 0,0017 
; 
фактическая длина намотки.
Учитывая это, получим:
(3.22)
где 
диаметр одной жилы;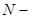 
количество витков обмотки; 
диаметр сердечника (
).
Тогда, учитывая данные примечания, получим:
Сопротивление провода круглого диаметра току высокой частоты можно вычислили по формуле
, (3.23)
где r0 – сопротивление постоянному току, Ом; F(z) – коэффициент, определяющий сопротивление с учетом поверхностного эффекта; G(z) – коэффициент, учитывающий эффект близости; N – количество витков намотки; D – диаметр каркаса; 
полный диаметр провода без наружной изоляции.
Значения коэффициентов F(z) и G(z) определены из таблицы [1]
Аргумент z определяется по формуле
(3.24)
где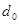 
– диаметр провода, мм; 
– частота Гц.
И равен: 
= 
При z=1,44: F(z)=1.183
G(z)=0.0369
Найдем численное значение 
:
Расчет сопротивления потерь в диэлектрике каркаса
Сопротивление потерь в диэлектрике каркаса вычислим по формуле
, (3.25)
где 
- емкость через диэлектрик, 
, пФ; 
тангенс угла диэлектрических потерь, для полистирола 
; 
фактическая индуктивность катушки, мкГн; частота, МГц; ε – диэлектрическая проницаемость полистирола (ε=2,5)
Экранирование катушки
|
|
|
Осуществим экранирование катушки с помощью замкнутого экрана цилиндрической формы, изготовленный из меди. По заданным размерам каркаса катушки (Dk, lk) и начальной индуктивности L0 определим Dэ (диаметр экрана) и его длину lэ.
Исходя из условия необходимо, чтоб имело силу равенство
Dэ- Dk= lэ- lk (
=0,45). (3.26)
При заданном находим Dэ, а из формулы (3.26) длину lэ
Тогда Dэ=10/0,45=22,22 мм
lэ= Dэ- Dk+ lk=22,22-10+25,73=37,95 мм
Толщину стенок экрана определим из источника (4):
t=0,1 мм
Расчет индуктивности после экранирования.
Индуктивность однослойной катушки L0 при размещении её в экране уменьшается и может быть определена по формуле:
Lэ=L0βL, (3.27)
где βL-коэффициент уменьшения индуктивности, определяемый по приближенной формуле:
βL 
(3.28)
Тогда
βL 
Вычислим Lэ:
Lэ=21,06∙0,81=17,05 мкГ
Найдем приращение индуктивности из формулы:
Lэ= L0- 
, (3.29)
где 
- приращение индуктивности; <0
= L0- Lэ=21.06-17.05=4.01.
Из формул (3.27) и (3.29) следует, что относительное уменьшение индуктивности составит:
относительное изменение составило 0,19, т.е. индуктивность катушки в экране изменилось на 19%. и равна 17,05 мкГн.
Расчет сопротивления, вносимого экраном
Вносимое экраном активное сопротивление с учетом поверхностного эффекта рассчитаем по формуле:
, (3.30)
где DЭ – диаметр экрана цилиндрической формы, 
- электропроводность материала экрана, 
(для меди 
=57∙106 ); 
- глубина проникновения материала экрана, см; N – число витков; Dк – диаметр катушки, см
Тогда,
Ом.
Определим относительное изменение активного сопротивления, оно составит:
, т. е. сопротивление возрастет на 0,00036%.
Расчет сопротивления потерь, вносимого сердечником
Определим сопротивление потерь вносимое сердечником по формуле:
, (3,31)
где 
- круговая частота; Lc – индуктивность сердечника; 
- тангенс угла потерь сердечника
Индуктивность сердечника рассчитаем по формуле:
Lc=μсL (3.32)
где μс –магнитная проницаемость сердечника;
L-фактическая индуктивность;
Тогда,
Lc=1,1∙21=23,1мкГ
Найдем численное значение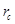 
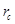= 2∙3,14∙5∙23,1∙2,4∙10-4=0,174Ом
Определим суммарное сопротивление потерь в катушке
– суммарное сопротивление потерь, определяется как:
|
|
|
, (3.33)
где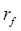 
– сопротивление провода току высокой частоты, характеризующие эффект близости и поверхностный эффект; 
– сопротивление, обусловленное влиянием экрана; 
– сопротивление потерь в диэлектрике каркаса;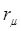 
– сопротивление, обусловленное потерями в сердечнике;
Тогда,
=1,99+0,0109+0,174+0,00001=2,17Ом
Расчет добротности катушки
По найденным сопротивлениям потерь определим добротность катушки индуктивности по формуле:
Q= 
(3.34)
Q= 
=193
|
|
|
