Высокотемпературные сверхпроводники в магнитном поле

Одним из важнейших параметров сверхпроводников второго рода являются нижнее (H_{C 1}) и верхнее (H_{C 2}) критическое поле, а также лондоновская глубина проникновения λ (п. 1.3). Эти параметры определяют поведение сверхпроводника в магнитном поле. Если напряженность приложенного магнитного поля (H_i) меньше H_{C 1}, то магнитное поле проникает в сверхпроводник на глубину порядка λ, как и в случае сверхпроводника первого рода (п. 1.2). Для образца, имеющего форму тонкой пластинки параллельной полю, магнитная индукция уменьшается с углублением на расстояние x:

B (x)= B (0)exp(- x / λ). (2.16)

Напряженность магнитного поля H_i вследствие эффектов размагничивания может существенно отличаться от внешнего поля H_e. В общем случае, при H_i < H_{C 1}, можно записать:

H ₁= H_e /(1- h), (2.17)

где h – размагничивающий фактор.

Размагничивающий фактор зависит от формы образца и его ориентации в магнитном поле. Например, для длинного цилиндра, пластины или очень вытянутого эллипсоида в продольном поле h =0. В поперечном поле для цилиндра h =0,5, для шара h =1/3, для пластины h ≈ 1.

Одной из основных особенностей ВТСП материалов является анизотропия свойств вдоль различных направлений. В соответствии с этим ВТСП соединения характеризуются тремя значениями как первого критического поля, так и глубины проникновения. Компоненты λ_a, λ_b и λ_c определяются величиной экранирующего тока вдоль соответствующих осей. В приближении квадратичного закона они связаны с анизотропными значениями эффективных масс с помощью соотношения:

, (2.18)

где m_{a , b , c} – компонента эффективной массы;

n – плотность куперовских пар.

Величина нижнего критического поля связана со значениями глубины проникновения в двух перпендикулярных полю направлениях:

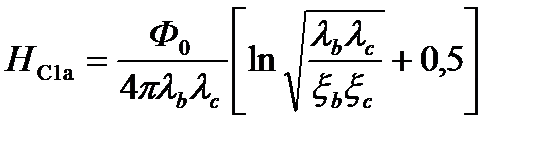, (2.19)

где ξ – компонента анизотропной длины когерентности;

Φ ₀ – квант магнитного потока.

Так же, как и все основные параметры сверхпроводников, глубина проникновения зависит от температуры. Для большинства сверхпроводников используется зависимость:

λ (T)= λ (0)/[1-(T / T_e)⁴]^1/2. (2.20)

Зависимость (2.20) оказывается близкой к зависимостям, полученным в модели БКШ для сильной связи.

Значения глубины проникновения у нижнего поля, для различных ВТСП материалов приведены в табл. 2.5.

Таблица 2.5

Значения параметров ВТСП материалов H_i<H_C1 [6].

Соединение	Ориентация	λ, нм	HC 1(0),э	dHC 1/ dT,э/к	Образец
Y-123	H | | C H_|_C H | | C H_|_C H | | C H_|_C – –	500-800 - - 140-170 205-250	- - - -	3,7 - - 3,1 4,4 - -	Монокристалл Монокристалл Керамика Керамика Ориентированная пленка Ориентированная пленка Ориентированная пленка Ориентированная пленка
Bi-2212	H | | C H_|_C H | | C H_|_C H | | C H_|_C – –	- - - -	- - - - - -	- - - - 2,1 - -	Монокристалл Монокристалл Монокристалл Монокристалл Монокристалл Монокристалл Керамика Керамика
Ti-2212	H | | C H_|_C –	- -	- - -	-	Монокристалл Монокристалл Керамика

 

Анализ таблицы показывает, что значения параметров для одного материала сильно отличаются друг от друга. Основной причиной этого, как нам представляется, служит различие в режимах обработки образцов.

После того, как поле H_i сравняется с H_{C 1}, вблизи поверхности образца возникают абрикосовские вихри, проникновение которых в толщу образца определяется характером пиннинга и поверхностным барьером. Диаметр вихря также определяется направлением поля и соответствующей компонентой глубины проникновения:

D =2 λ_i. (2.21)

Для анизотропных сверхпроводников проникновение абрикосовских вихрей в образец имеет аномальный характер. Он проявляется прежде всего в том, что при направлении магнитного поля, отличного от главных осей кристалла, проникающие вихри отклоняются от направления поля. Этот факт необходимо учитывать, проектируя континуальную среду криоэлектронных устройств на одиночных вихрях. При дальнейшем увеличении поля увеличивается его проникновение в образец, и при Н_i = H_{C 2} сверхпроводник переходит в нормальное состояние. Такое поле называют вторым критическим полем. ВТСП относятся к материалам с большими значениями параметра Гинзбурга-Ландау (χ=λ/ξ₀ ) и верхнего критического поля H_{C 2}. По измерениям H_C2 можно оценить продольную (ξ _{| |} ) и перпендикулярную (ξ _{_|_}) компоненты длины когерентности. С учетом того, что m_a = m_b << m_c, в условиях близости к критической температуре, из выражений для свободной энергии системы можно получить зависимость H_{C 2} от угла между осью с и внешним полем H_e:

. (2.22)

Из (2.22) можно получить выражение для параллельной (θ =0) и перпендикулярной (θ = π /2) ориентации поля относительно оси с:

H_{C 2| |}=Φ₀/2π ξ _{| |} ξ _{_|_} , (2.23)

H_{C 2 _|_} =Φ₀/2π ξ _{| |}². (2.24)

В случае более низких температур длина когерентности уменьшается и становится сравнимой с расстоянием между плоскостями СuО или даже меньше этого расстояния:

ξ _{_|_} (T) ~ (1- T / T_C)^-1/2 (2.25)

Чаще всего верхние критические поля H_{C 2} определяют по изменению температурной зависимости сопротивления образца (см. рис. 2.21).

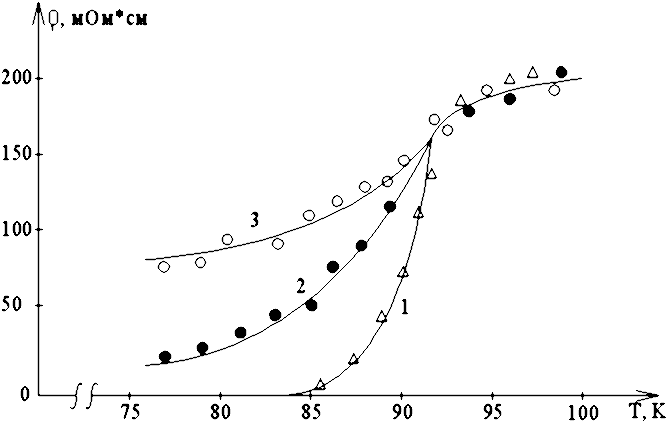
Рис. 2.21. Температурная зависимость сопротивления Bi-2212: 1 – 0 Тл; 2 – 4 Тл(||); 3 – 4 Тл(_|_)

Их характерной особенностью является сильная размытость, которая даже у монокристаллов может достигать десятков градусов. Поэтому часто кривую H_{C 2}(T) характеризуют значением скорости изменения dH_{C 2}/ dT. В табл. 2.6 приведены значения скорости dH_{C 2 | |} / dT и dH_{C 2_|_}/ dT, а также значения длины когерентности ξ_{0| |} и ξ_{0_|_}.

Таблица 2.6

Результаты резистивных измерений в различных сверхпроводниках [5]

Соединение	Tkc, К	dHC 2| |/ dT, Тл/К	dHC 2_|_ dT, Тл/К	ξ0| |, А0	ξ0_|_,А0
Y-123	92,7	3,8 3,9 5,6 3,12	0,54 1,1 0,9 0,32	4,3 4,9
Bi-2212	80,6	4,9 – 7,3	0,4 – 0,55 0,39	2,1 – 3,6	34 – 40
Tl-2212		1,9 1,1	0,2 0,25

 

Анализ таблицы показывает, что расхождение в оценке одного параметра для различных образцов имеет место, вероятно, вследствие разных условий изготовления.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: