 |
Дифференциальные уравнения
|
|
|
|
Глава 6. Динамика НМС
Дифференциальные уравнения
Поступательного движения НМС
Одним из наиболее эффективных методов изучения движения НМС под действием приложенных к ней сил является метод, основанный на применении общих теорем динамики СМТ. Изучение кинематики поступательного движения НМС (Ч.1 Кинематика) показало, что исследование поступательного движения НМС сводится к рассмотрению движения любой ее МТ. Взяв в качестве такой МТ центр масс С (соотношение (4.18)), на основании теоремы о движении центра масс можно записать дифференциальные уравнения поступательного движения НМС в виде:
(6.1)
При движении центра масс НМС в одной плоскости, например xOy, дифференциальные уравнения поступательного движения НМС будут представлены двумя первыми уравнениями из соотношений (6.1).
Дифференциальное уравнение вращательного движения НМС относительно неподвижной оси
Пусть на НМС, имеющую неподвижную ось вращения z и оси х и у жестко связанных с НМС, действует система внешних сил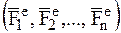 
. Использовав аксиому 5 статики – принцип освобождаемости (Ч.2 Статика), заменим действие связей в подпятнике О и подшипнике В силами реакции связи 
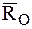и 
(рис. 43).
Чтобы получить дифференциальное уравнение вращательного движения НМС относительно неподвижной оси Оz, применим теорему об изменении кинетического момента СМТ – третье уравнение соотношений (4.25):
.
Рис. 43
Так как реакци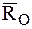и и пересекают ось z, то
и, следовательно,
. (6.2)
Подставляя в уравнение (6.2) значение кинетического момента НМС в случае вращательного движения вокруг неподвижной оси (4.28): 
, получим:
.
Для НМС момент инерции JОz = const и, следовательно,
, 
, 
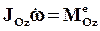. (6.3)
|
|
|
Уравнения (6.3) представляют собой различные формы записи уравнения вращательного движения НМС вокруг неподвижной оси.
На основании третьего соотношения (6.3) можно сделать вывод, что при данном значении вращательного момента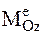 
, чем больше 
– момент инерции НМС относительно оси вращения, тем меньше e – угловое ускорение НМС и наоборот. Следовательно, момент инерции является мерой инертности НМС при ее вращательном движении вокруг неподвижной оси Оz.
Физический маятник
Физическим маятником называется АТТ произвольной формы, вращающееся только под влиянием силы тяжести 
вокруг неподвижной горизонтальной оси, не проходящей через центр масс АТТ. Горизонтальную ось вращения примем за ось Оz, а за плоскость xОy – вертикальную плоскость (ось Ох вертикальна), перпендикулярную оси Оz и проходящую через центр тяжести С маятника (рис. 44).
Рис. 44
Точку О назовем точкой подвеса физического маятника, а расстояние ОС от центра тяжести до точки подвеса обозначим через а. Положение маятника определяется углом отклонения j линии ОС от вертикали.
Используя второе из уравнений (6.3), получим уравнение движения физического маятника в виде:
. (6.4)
Полагая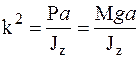 
, где М – масса физического маятника, представим (6.4) в виде:
.
Ограничиваясь изучением малых колебаний физического маятника, для которого можно положить 
, имеем:
. (6.5)
Из уравнения (6.5) видно, что малые колебания физического маятника являются гармоническими. Период малых колебаний физического маятника определяется из равенства:
. (6.6)
Сравнивая формулу для периода малых колебаний плоского математического маятника (пример 4 главы 1, п. 1.4)
с полученной формулой (6.6) периода малых колебаний физического маятника, найдем, что при длине
(6.7)
их периоды совпадают.
Определение: Длина l такого математического маятника, период малых колебаний которого равен периоду малых колебаний данного физического маятника, называется приведенной длиной физического маятника.
|
|
|
Точка О1, отстоящая от точки подвеса О на расстоянии
ОО1 = l, называется центром качания физического маятника.
Согласно теореме Штейнера-Гюйгенса (3.22), имеем:
,
где 
– момент инерции АТТ относительно оси, проходящей через центр масс С и параллельной оси Оz. Подставив это соотношение в формулу (6.7), для приведенной длины физического маятника будем иметь:
, (6.8)
где
. (6.9)
Из соотношения (6.8) следует, что приведенная длина l = ОО1 физического маятника всегда больше расстояния а = ОС (рис. 44).
Найдем приведенную длину физического маятника l1 в том случае, когда ось подвеса z1 проходит через центр качаний О1.
В этом случае приведенная длина физического маятника по аналогии с соотношением (6.8) примет вид:
, (6.10)
где 
из соотношения (6.9).
Таким образом, колебания физического маятника имеют одинаковый период для осей вращения, проходящих через точку подвеса О и точку качания О1 (расстояние между этими точками равно приведенной длине физического маятника).
Дифференциальные уравнения
|
|
|
