 |
Методы расчета блокирующих коммутационных систем
|
|
|
|
Этот раздел содержит три части, которые объединяет в единое целое звеньевой способ построения коммутационных систем.
При изучении этого раздела в первую очередь следует уяснить физическую сущность внутренних блокировок звеньевых схем. А затем разобраться в идеях метода эффективной доступности, применяемой для расчета двухзвенных схем. Следует уяснить смысл метода вероятностных графов, который используется для определения потерь сообщения в многозвенных коммутационных схемах.
Материал этого раздела изложен на страницах 140-172 в [1], расчет многозвенных схем методом вероятностных графов дан в [2], [3].
Для закрепления материала раздела рекомендуется ответить на следующие вопросы:
1. Внутренние блокировки, способы их уменьшения.
2. Изменение доступности по причине внутренних блокировок на примере двухзвенной схемы.
3. Расчет числа соединительных устройств, включаемых в двухзвенные схемы.
4. Режимы использования коммутационных схем. Схемы возможных путей соединения в двухзвенной системе при различных режимах искания.
5. Определение потерь сообщения в звеньевых схемах методом вероятностных графов.
6. Структуры многозвенных КС. Способы межзвеньевых соединений и методы искания.
7. Оптимизация многозвенных КС. Результаты Лотце.
8. Расчет потерь в многозвенных КС. Методы КЛИГС и ППЛ.
Приложение теории телетрафика к исследованию сетей связи
Четвертый раздел содержит пять частей. При изучении первых трех частей надо научиться определять суммарные потери сообщения при установлении соединения через несколько ступеней искания.
Нужно знать нормы потерь на городских, сельских и междугородных телефонных сетях и уметь их обосновывать. Следует усвоить методику распределения нагрузки по ступеням искания и направлениям и распределения нагрузки между станциями сети, а также методику расчета нагрузки на управляющие устройства. Вопрос о расчетной нагрузке надо рассматривать в связи с колебаниями нагрузки по абонентским группам, направлениям т по различным ЧНН.
|
|
|
Материал этих частей раздела изложен на страницах 172-189 в [1].
При проработке четвертой и пятой частей раздела следует обратить внимание на способы увеличения пропускной способности сети связи путем введения обходных направлений и динамического управления потоками нагрузки.
Эти вопросы изложены на страницах 190-203 в [1]. Для закрепления материала раздела рекомендуется ответить на следующие вопросы.
1. Распределение потерь по ступеням искания. Суммирование потерь.
2. Колеблемость нагрузки. Расчетная интенсивность нагрузки.
3. Способы распределения межстанционных потоков телефонной нагрузки.
4. Определение пропускной способности маркера.
5. Способы управления, применяемые на сетях связи.
6.Расчет обходных направлений в сетях связи. Результаты Вилкинсона
Метод статистического моделирования для решения задач теории телетрафика
В этом разделе следует обратить внимание на необходимость применения статистического моделирования и уяснить задачи, решаемые при помощи статистического моделирования на ЭВМ. Достоинства и недостатки метода.
Этот вопрос изложен на страницах 106-116 в [1], а также в [2], [3], [10], [11].
Методы измерения параметров информационного сообщения
Здесь надо выяснить назначение и способы измерений нагрузки, ознакомиться со способами обработки полученных результатов.
Материал этого раздела изложен на страницах 203-213 в [1].
Для закрепления материала пятого и шестого разделов рекомендуется ответить на следующие вопросы.
|
|
|
1. Укажите причины, которые обуславливают применение различных способов управления на сетях связи.
2. Назовите способы управления сетями связи и их особенности.
3. Укажите основные цели измерения параметров нагрузки и потерь.
4. Перечислите типы ошибок, которые следует учитывать при измерении параметров нагрузки и потерь.
КУРСОВАЯ РАБОТА.
3.1Общие указания и выбор варианта.
Курсовая работа предназначена для развития навыков студентов по решению конкретных практических вопросов на основе полученных знаний при изучении курса. Одновременно выполнение КР способствует более глубокому усвоению материала, связанного с задачами курса.
Перед выполнением каждой задачи необходимо изучить ту часть курса, которая относится к этой задаче. Выполнять задачи нужно вдумчиво и уметь обосновывать полученный результат. На защите проводится собеседование по выполненным работам.
Каждый студент выполняет семь задач в одном варианте. Номер варианта равен сумме двух последних цифр номера студенческого билета. Например, номер студенческого билета А-79206. Номер варианта равен 0+6=6.
Требования к оформлению.
При выполнении и оформлении КР следует иметь в виду, что КР необходимо выполнить в отдельной тетради, обязательно чернилами. Страницы тетради должны быть пронумерованы, необходимо выделить поля для замечаний рецензента. Решения задач следует располагать в порядке номеров, указанных в заданиях, перед решением каждой задачи необходимо написать условие задачи для требуемого варианта. Каждый студент должен выполнить КР в одном варианте, причем номер варианта должен соответствовать тем указаниям, которые имеются в контрольных заданиях. КР, выполненные не по требуемому варианту, не зачитываются. Решения задач должны быть четкими, пояснения краткими, но без сокращения слов. В случае необходимости нужно делать ссылки на теорию, указывая учебник, автора, год издания, страницу и если необходимо, номер чертежа.
Чертежи в КР должны быть выполнены аккуратно, с помощью линейки и циркуля и, если это требуется условием задачи, с соблюдением масштаба. Все чертежи, рисунки, таблицы должны быть пронумерованы.
Расчетные формулы следует приводить в тексте работы в общем виде с объяснением входящих в них буквенных значений. Все числовые значения необходимо представить только в основных единицах (вольт, ампер и т.д.).
|
|
|
КР, выполненные небрежно, без промежуточных вычислений, с пропуском задач, возвращаются студенту обратно для переработки.
В конце каждой КР необходимо указать учебники и учебные пособия, которыми пользовался студент. Работы должны быть подписаны студентом, с указанием даты выполнения.
После выполнения и оформления КР должна быть выслана на проверку в СибГУТИ.
При получении прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и выполнить все сделанные им указания. Если работа не зачтена, то ее необходимо после переделки, в соответствии с требованиями рецензента, выслать на повторную рецензию.
Без предъявления зачтенных работ студент к сдаче экзамена не допускается.
СОДЕРЖАНИЕ ЗАДАЧ.
Задача 1. На коммутационную систему поступает поток вызовов, создающий нагрузку Y эрланг. Определить вероятности поступления ровно i вызовов Pi (i=0, 1, 2...N) при примитивном потоке от N источников и Pi (i=0,1, 2...j...) при простейшем потоке вызовов. Построить кривые распределения вероятностей Pi =f (i) и произвести сравнение полученных результатов. Вычислить математическое ожидание числа вызовов на единичном интервале для простейшего и примитивного потоков вызовов. Сравнить результаты и сделать выводы. Величины Y и N приведены в табл.1
Таблица 1
| Номер варианта | |||||||||
| Y, эрл | 1,8 | 2,4 | 4,0 | 3,6 | 3,6 | 2,1 | 2,8 | 2,8 | 4,5 |
| N |
| Номер варианта | ||||||||||
| Y, эрл | 1,5 | 2,0 | 1,8 | 3,2 | 5,0 | 2,1 | 4,7 | 4,3 | 3,5 | 4,5 |
| N |
Задача 2. Рассчитать величину возникающей на цифровой АТС нагрузки от абонентов следующих категорий:
-Nн (индивидуального пользования);
-Nнд(народно-хозяйственного сектора «делового»)
-Nнс(народно-хозяйственного сектора «спального»)
|
|
|
-Nт.мест(таксофонов местной связи)
-Nт.межд(таксофонов междугородних. Исходящая связь)
-Nрпп(районных переговорных пунктов)
-Nф(факсимильных аппаратов. Соединение по телефонному алгоритму)
-Абонентов ЦСНО с доступами:
типа 2В+D
типа 30В+D
При определении возникающей нагрузки следует учесть нагрузку на ЗСЛ и УСС.
Город с населением свыше 1 млн жителей.
Нумерация на ГТС шестизначная.
Исходные данные сведены в табл.2
Таблица 2.
Задача 3. Полнодоступный пучок из V линий обслуживает поток вызовов. Определить нагрузку Y, которая может поступать на этот пучок при заданной величине потерь по вызовам PВ
в случае простейшего потока и примитивного потока от N1 и N2 источников. Значения V, PB, N1 и N2 приведены в таблице 3. По результатам расчета сделать выводы.
Таблица 3
| Номер варианта | |||||||||
| V | |||||||||
| PB,%0 | |||||||||
| N1 | |||||||||
| N2 |
| Номер варианта | ||||||||||
| V | ||||||||||
| PB,%0 | ||||||||||
| N1 | ||||||||||
| N2 |
Задача 4. На вход коммутационной системы поступает нагрузка по двум пучкам линий, математическое ожидание которой Y1 и Y2. На выходе ступени объединенная нагрузка распределяется по направлениям пропорционально коэффициентам Ki. определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. По результатам расчета сделать вывод. Исходные данные приведены в табл.4.
Таблица 4
| Номер варианта | |||||||||
| Y1, Эрл. | |||||||||
| Y2, Эрл. | |||||||||
| K1 | 0,2 | 0,15 | 0,1 | 0,2 | 0,25 | 0,1 | 0,1 | 0,12 | 0,1 |
| K2 | 0,3 | 0,2 | 0,15 | 0,2 | 0,35 | 0,15 | 0,17 | 0,34 | 0,35 |
| K3 | 0,5 | 0,25 | 0,3 | 0,25 | 0,4 | 0,25 | 0,27 | 0,54 | 0,55 |
| K4 | - | 0,4 | 0,45 | 0,35 | - | 0,5 | 0,46 | - | - |
| Номер варианта | ||||||||||
| Y1, Эрл. | ||||||||||
| Y2, Эрл. | ||||||||||
| K1 | 0,1 | 0,2 | 0,15 | 0,1 | 0,15 | 0,1 | 0,13 | 0,15 | 0,1 | 0,1 |
| K2 | 0,2 | 0,35 | 0,2 | 0,25 | 0,25 | 0,15 | 0,20 | 0,35 | 0,3 | 0,15 |
| K3 | 0,3 | 0,45 | 0,3 | 0,3 | 0,6 | 0,35 | 0,27 | 0,5 | 0,6 | 0,3 |
| K4 | 0,4 | - | 0,35 | 0,35 | - | 0,4 | 0,4 | - | - | 0,45 |
Задача 5. На V-линейную СМО поступают простейший поток вызовов с параметром  (выз/час). Вызовы обслуживаются системой с ожиданием. Время обслуживания распределено экспоненциально со средним значением
(выз/час). Вызовы обслуживаются системой с ожиданием. Время обслуживания распределено экспоненциально со средним значением  . Допустимое время задержки вызова -
. Допустимое время задержки вызова - 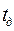 (с)
(с)
|
|
|
Определить вероятности занятости i линий в произвольный момент времени  ;вероятность того, что длина очереди составит j-вызовов
;вероятность того, что длина очереди составит j-вызовов  -
-  ; Функцию распределения времени ожидания начала обслуживания -
; Функцию распределения времени ожидания начала обслуживания - 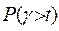 ; среднее время ожидания начала обслуживания -
; среднее время ожидания начала обслуживания -  ; среднюю длину очереди -
; среднюю длину очереди -  .
.
По результатам расчетов сделать выводы. Исходные данные приведены в таблице 5.
Таблица 5.
| № варианта | ||||||||||
 , выз/час , выз/час
| ||||||||||
| t,с | ||||||||||
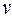
| ||||||||||
| tд ,с |
| № варианта | |||||||||
 , выз/час , выз/час
| |||||||||
| t,с | |||||||||
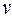
| |||||||||
| tд ,с |
Задача 6. На однолинейную СМО (V=1) поступает простейший поток вызовов с параметром  (выз/час). Среднее время обслуживания каждого вызова h(c) Вызовы обслуживаются в системе с ожиданием в порядке их поступления (в порядке очереди). Максимальная длина очереди (емкость накопителя) не ограничена.
(выз/час). Среднее время обслуживания каждого вызова h(c) Вызовы обслуживаются в системе с ожиданием в порядке их поступления (в порядке очереди). Максимальная длина очереди (емкость накопителя) не ограничена.
Исходные данные сведены в таблице 6.
О пределить:
для модели М/D/1
- У- поступающую на СМО нагрузку;
- P( >0) – вероятность обслуживания с ожиданием;
>0) – вероятность обслуживания с ожиданием;
- М[  ] – среднее время ожидания начала обслуживания для любого поступившего вызова в относительных и абсолютных величинах;
] – среднее время ожидания начала обслуживания для любого поступившего вызова в относительных и абсолютных величинах;
- M[  ] – тоже для задержанных вызовов;
] – тоже для задержанных вызовов;
- M[Т] – среднее время пребывания в СМО задержанных вызовах;
- M[j] – среднюю длину в очереди;
- M[j]’ – среднее число вызовов в СМО;
для модели М/М/1
- У- поступающую на СМО нагрузку;
- P( >0) – вероятность обслуживания с ожиданием;
>0) – вероятность обслуживания с ожиданием;
- P( >t) – функцию распределения времени ожидания начала обслуживания;
>t) – функцию распределения времени ожидания начала обслуживания;
- М[  ] – среднее время ожидания начала обслуживания для любого поступившего вызова в относительных и абсолютных величинах;
] – среднее время ожидания начала обслуживания для любого поступившего вызова в относительных и абсолютных величинах;
- M[  ] – тоже для задержанных вызовов;
] – тоже для задержанных вызовов;
- M[Т] – среднее время пребывания в СМО задержанных вызовах;
- M[j] – среднюю длину в очереди;
- M[j]’ – среднее число вызовов в СМО;
Для модели FBD/D/1
- М[  ] – среднее время ожидания начала обслуживания для любого поступившего вызова;
] – среднее время ожидания начала обслуживания для любого поступившего вызова;
- M[Т] – среднее время пребывания вызова в СМО;
- M[j] – средняя длина очереди;
- M[j]’ – среднее число вызовов в СМО
Выводы должны содержать комментарии вычисляемых параметров и сравнение трех исследуемых моделей обслуживания.
Таблица 6.
| № варианта | ||||||||||
 , выз/час , выз/час
| ||||||||||
| h,с | ||||||||||
| tд ,с |
| № варианта | |||||||||
 , выз/час , выз/час
| |||||||||
| h,с | |||||||||
| tД ,с |
Задача №7 На однолинейную СМО(V=1) с показательныем временем обслуживания поступают 3 простейших потока вызовов (n=3) с параметрами  и приоритетами обслуживания К=1,2,3(с увеличением К приоритет убывает), интенсивность времени обслуживания вызова
и приоритетами обслуживания К=1,2,3(с увеличением К приоритет убывает), интенсивность времени обслуживания вызова  соответственно. Дисциплина обслуживания входящих потоков с ожиданием. Длина очереди не ограничена.
соответственно. Дисциплина обслуживания входящих потоков с ожиданием. Длина очереди не ограничена.
Определить:
-среднее время обслуживания вызовов каждого потока 
-интенсивность нагрузки поступающей на СМО  и
и 
-среднее время ожидания начала обслуживания и среднее время пребывания в СМО для вызовов каждого потока в случае:
1) безприоритетного обслуживания
2) обслуживания с относительным приоритетом
3) обслуживания с абсолютным приоритетом с дообслуживанием.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КР.
Решение задачи 1 имеет своей целью закрепление материала по изучению математических моделей простейшего и примитивного потоков вызовов. К ее выполнению можно приступить после проработки первой части раздела программы.
Вероятностный процесс поступления вызовов простейшего потока описывается формулой (распределения) Пуассона:

а примитивного - распределение Бернулли:

где а=  - нагрузка, поступающая от одного источника.
- нагрузка, поступающая от одного источника.
Примитивный поток создается конечным числом источников, а простейший - теоретически бесконечным числом источников вызовов (практически достаточно, чтобы N было больше 100). Расчет распределения Пуассона и Бернулли целесообразно вести в следующей последовательности. Сначала, полагая i=0, определяют вероятность отсутствия вызовов Р0. Остальные Рi находят по рекурентным формулам:
 ; (j=0, 1, 2...) - для простейшего потока,
; (j=0, 1, 2...) - для простейшего потока,
 ; (j=0, 1, 2...) - для примитивного потока,
; (j=0, 1, 2...) - для примитивного потока,
где j+1=i.
Максимальное значение i при расчете Рi для простейшего потока принять равной заданному N для примитивного потока.
Задача 2 Согласно РД 45.120-2000, расчет возникающей нагрузки производится отдельно для утреннего и вечернего ЧНН, после чего среди них выбирается максимальное значение, которое принимается за расчетную нагрузку.
Расчет утреннего ЧНН
Yутр = Уi утр.ЧНН+Уj утр.вр.,
Где: Уi утр.ЧНН – суммарная нагрузка для всех i категорий абонентов, имеющих утренний ЧНН;
Уiутр.ЧНН = Ni*Yi, где: Ni – число источников категории i;
Yi – интенсивность удельной нагрузки абонента i-ой категории(см табл.8);
Уj утр.вр - суммарная нагрузка, создаваемая во время утреннего ЧНН, абонентами j-ой категории, имеющих вечерний ЧНН;
Уj утр.вр = Уj веч.ЧНН/1,6; Уj веч.ЧНН = Nj*Yj.
Таблица 8. Исходные данные
| Категория | У,Эрл | Время ЧНН |
| 1.Индивидуального пользования | 0.022 0.03 | Утр. ЧНН Веч. ЧНН |
| 2.Народно- хозяйственный Деловой Спальный | 0.07 0.03 | Утр. ЧНН, Веч. Вр. Веч. ЧНН, Утр Вр. |
| 3.Таксофоны местной связи | 0.2 0.27 | Дневной ЧНН Вечерний ЧНН |
| 4.. Таксофоны междугородние | 0.65 0.65 | Дневной ЧНН Вечерний ЧНН |
| 5.РПП | 0.6 | Веч. ЧНН, Утр Вр. |
| 6. Факс по ТЛФ. Алгоритму | 0.15 | Утр. ЧНН, Веч. Вр. |
| 7. Абонент ЦСНО 2B+D 30B+D | 0.25 0.12 | Утр. ЧНН, Веч. Вр. Утр. ЧНН, Веч. Вр. |
Аналогично рассчитывается нагрузка в вечерний ЧНН.
Yвеч = Уj веч.ЧНН + Уi веч.вр.,
Нагрузку создаваемую таксофонами с дневным ЧНН, следует относить к максимальному ЧНН (Утреннему или вечернему).
Нагрузка на ЗСЛ, учитывая число жителей в городе свыше 106 человек:
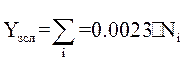
Где: Ni – число источников i-ой категории, имеющих право установления междугородней связи.
Нагрузка на УСС принимается в размере 5% от максимальной утренней или вечерней.
Таким образом, общая возникающая на АТС нагрузка равна:

Задача 3 выполняется после изучения первой части второго раздела программы. Решение этой задачи преследует цель показать зависимость пропускной способности полнодоступного пучка линий от характера (класса) поступающего потока вызовов.
Обслуживание полнодоступным пучком простейшего потока описывается первой формулой Эрланга: формула (4.28) в [1], а примитивного потока - формулой Энгсета: (4.38)
по причине сложности расчета пропускной способности по формулам Эрланга и Энгсета (они не решаются относительно y) рекомендуется пользоваться таблицами Пальма [4] (приложение 3) для простейшего потока (табулированная формула Эрланга), что касается таблиц формулы Энгсета, то они встречаются реже. Поэтому в приложениях 1 и 2 данного УМД приведены соответственно значения функций Эрланга и Энгсета, необходимые для решения этой задачи.
Заметим, что здесь, как в первой задаче y=l для простейшего потока и y=aN для примитивного потока, где а- нагрузка, поступающая от одного источника.
Решить задачу 4 следует после изучения второй части раздела 4 программы.
Расчетная нагрузка учитывает колеблемость нагрузки. Поступающей на пучок соединительных устройств заданной емкости. Ее значение определяется по формуле (10.47) в [1].
По результатам расчета рекомендуется сделать вывод о величине относительного отклонения расчетной нагрузки от ее математического ожидания в зависимости от величины математического ожидания нагрузки
di=  ,
,
где Yi,p- расчетное значение нагрузки в направлении i.
Yi - среднее (математическое ожидание) в этом же направлении.
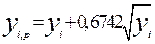
Задачу 5 следует решать после изучения разделов 6,7 программы. Приводим последовательность вычислений.
1.Нагрузка поступающая на СМО

2.По таблице Пальма (приложение 1) находим значение  .
.
3.Вычисляем 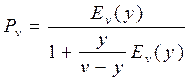
4.По рекуррентной формуле  находим остальные значения
находим остальные значения 

5.Вероятность  . Остальные значения
. Остальные значения  вычисляем по формуле
вычисляем по формуле
 .
. 
6.По формуле  вычисляем потери по времени.
вычисляем потери по времени.
7.Функция распределения времени задержки  ,где
,где 
8.Среднее время задержки в относительных единицах ( ).
).
 ; в абсолютных
; в абсолютных 
9.Средняя длина очереди  ;
;
10.Выводы по результатам решения.
Указания к решению задачи 6
а)Модель обслуживания М/D/1.
-  ;
; 
-  ; -в относительных единицах
; -в относительных единицах
 - в абсолютных единицах(с)
- в абсолютных единицах(с)
- 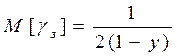 ; - в относительных единицах.
; - в относительных единицах.
 - в абсолютных единицах(с)
- в абсолютных единицах(с)
-  ;
;

 .
.
б) модель обслуживания М/М/1.
-  ; где,
; где,  ;
;
- 
- 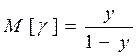 ;
;  (с)
(с)
-  ;
;  (с)
(с)
-  ;
;
- 
- 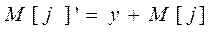
в) модель FBD/D/1
 ;
;




 ;
;
Этот пункт выполняется для двух значений параметра Хёрсте(H1=0.6; H2=0.8)
В выводах указать на характер влияния параметра H на величину задержки.
Задача 7 выполняется в следующей последовательности.
1. СМО без приоритетов
Базовая модель  - формула Хинчина. (результат в абсолютных единицах).
- формула Хинчина. (результат в абсолютных единицах).
 ;
;
для модели 
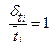
тогда  ;
;
где: n – число входящих потоков;

n- число входящих потоков;

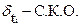
С использованием второго начального момента  для модели
для модели 
 ;
;

тогда

получим одинаковый результат.
2.СМО с относительным приоритетом 
Базовая формула:

где: к – номер приоритета (с увеличением «К» приоритет уменьшается)
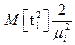


где

тогда

для n=3; k=1,2,3 имеем
 ;
; 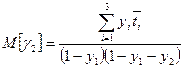 ;
;
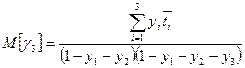 ;
;
3. Абсолютный приоритетс дообслуживанием
базовая формула

где: к – номер приоритета.
Для n = 3; к = 1, 2, 3 имеем.

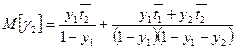

среднее время пребывания вызова в СМО - 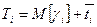

Результат вычислений по приведенным формулам в абсолютных единицах.
|
|
|


