 |
Операции над комплексными числами
|
|
|
|
Билет №1
1) Определение модели.
модель – это объект-заместитель объекта-оригинала, обеспечивающий изучение определенных свойств оригинала.
2) Представление системы алгебраических уравнений в матричном виде и её решение.
Билет №2
1) Физическое моделирование.
Под физическим моделированием понимают процесс установления реальному объекту некоего макета, сохраняющего физическую природу исследуемого объекта. Физическое моделирование используют в архитектуре, гидротехнике.
Например, при проектирование турбины создают ее физическую модель – уменьшенный макет реальной турбины, посредством которого может изучить поведение реальной турбины.
2) Запишите формулу для разложения функции в ряд Тейлора.
Для оценки погрешности интегрирования  разложим подынтегральную функцию
разложим подынтегральную функцию  в ряд Тейлора около средней точки
в ряд Тейлора около средней точки 
 . (5.26)
. (5.26)
В малой окрестности точки x в разложении (5.26) можно ограничится небольшим количеством членов ряда.
Билет №3
1) Математическое моделирование
Под математическим моделированием понимают процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получить характеристики рассматриваемого реального объекта.
Например, переходные процессы в системе управления турбиной можно описать с помощью дифференциальных уравнений, т.е. математической модели данного исследуемого объекта (турбины).
При этом следует отметить, что любая математическая модель описывает процесс функционирования реального объекта лишь с некоторой степенью приближения к действительности. Математическое моделирование исследования процесса функционирования системы можно разделить на аналитическое и имитационное.
|
|
|
Исторически первым появилось аналитическое моделирование, для которого характерно то, что процессы функционирования элементов системы записываются в форме некоторых функциональных соотношений (алгебраических, дифференциальных, конечно-разностных и т.п.).
При использовании имитационного моделирования воспроизводится процесс функционирования системы во времени, причем имитируются элементарные явления при сохранении их логической структуры и последовательности протекания во времени.
Это позволяет по исходным данным получить сведения о состоянии исследуемого процесса в определенные моменты времени. Основное преимущество имитационного моделирования – возможность решения более сложных задач. Имитационные модели позволяют учитывать наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия.
2) Вычисление интеграла с заданной точностью.
Вычисление интеграла с заданной точностью. Используя приведенные выше оценки можно априори (до проведения расчета) определить шаг интегрирования h, при котором погрешность вычисленного результата гарантированно не превысит допустимый уровень погрешности e. Однако на практике пользоваться априорными оценками погрешности не всегда удобно. Тогда контроль за точностью получаемого результата можно организовать следующим образом. Пусть вычисления проводились с постоянным шагом h, 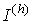 – вычисленное с шагом h приближенное значение интеграла I. Если затем вычислить приближенное значение
– вычисленное с шагом h приближенное значение интеграла I. Если затем вычислить приближенное значение  с шагом
с шагом  , то в качестве оценки погрешности последнего вычисленного значения можно рассматривать величину
, то в качестве оценки погрешности последнего вычисленного значения можно рассматривать величину
 .
.
При необходимости вычислить результат с заданной точностью e вычисления повторяют с последовательно уменьшающимся (вдвое) шагом до тех пор, пока не выполнится условие
|
|
|
 . (5.30)
. (5.30)
Можно применить указанное правило для контроля за локальной погрешностью на каждом частичном интервале. При этом длина очередного интервала  , посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
, посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
рассматривать величину
 .
.
При необходимости вычислить результат с заданной точностью e вычисления повторяют с последовательно уменьшающимся (вдвое) шагом до тех пор, пока не выполнится условие
 . (5.30)
. (5.30)
Можно применить указанное правило для контроля за локальной погрешностью на каждом частичном интервале. При этом длина очередного интервала  , посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
, посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
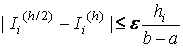 . (5.31)
. (5.31)
Тогда в худшем случае ошибка вычисленного значения интеграла на всем интервале интегрирования не будет превосходить сумму локальных погрешностей  , т.е. не будет превосходить заданного уровня погрешности.
, т.е. не будет превосходить заданного уровня погрешности.
Способ вычисления интеграла с автоматическим выбором шага имеет то преимущество, что он “приспосабливается” к особенностям подынтегральной функции: в областях резкого изменения функции шаг уменьшается, а там, где функция меняется слабо, – увеличивается. Такого рода алгоритмы называются адаптивными, т.е. приспосабливающимися. Использование адаптивных алгоритмов позволяет сократить затраты машинного времени без потери точности.
Билет №4
1) Представление системы алгебраических уравнений в матричном виде и её решение.
2) Виды файлов в MATLAB.
Билет №5
1) Запишите формулу для разложения функции в ряд Тейлора.
Для оценки погрешности интегрирования  разложим подынтегральную функцию
разложим подынтегральную функцию  в ряд Тейлора около средней точки
в ряд Тейлора около средней точки 
 . (5.26)
. (5.26)
В малой окрестности точки x в разложении (5.26) можно ограничится небольшим количеством членов ряда.
2) Решение нелинейных уравнений численными методами.
Билет №6
1) Запишите вычислительный алгоритм для решения дифференциального уравнения методом Эйлера.
|
|
|
2) Интерполяция.
Билет №7
1) Формы записи комплексных чисел.
2) Численное дифференцирование.
Билет №8
1) Решение нелинейных уравнений численными методами.
2) Численное интегрирование.
Билет №9
1) Вычисление интеграла с заданной точностью.
Вычисление интеграла с заданной точностью. Используя приведенные выше оценки можно априори (до проведения расчета) определить шаг интегрирования h, при котором погрешность вычисленного результата гарантированно не превысит допустимый уровень погрешности e. Однако на практике пользоваться априорными оценками погрешности не всегда удобно. Тогда контроль за точностью получаемого результата можно организовать следующим образом. Пусть вычисления проводились с постоянным шагом h, 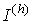 – вычисленное с шагом h приближенное значение интеграла I. Если затем вычислить приближенное значение
– вычисленное с шагом h приближенное значение интеграла I. Если затем вычислить приближенное значение  с шагом
с шагом  , то в качестве оценки погрешности последнего вычисленного значения можно рассматривать величину
, то в качестве оценки погрешности последнего вычисленного значения можно рассматривать величину
 .
.
При необходимости вычислить результат с заданной точностью e вычисления повторяют с последовательно уменьшающимся (вдвое) шагом до тех пор, пока не выполнится условие
 . (5.30)
. (5.30)
Можно применить указанное правило для контроля за локальной погрешностью на каждом частичном интервале. При этом длина очередного интервала  , посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
, посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
рассматривать величину
 .
.
При необходимости вычислить результат с заданной точностью e вычисления повторяют с последовательно уменьшающимся (вдвое) шагом до тех пор, пока не выполнится условие
 . (5.30)
. (5.30)
Можно применить указанное правило для контроля за локальной погрешностью на каждом частичном интервале. При этом длина очередного интервала  , посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
, посредством последовательного уменьшения (или увеличения) начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
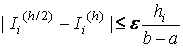 . (5.31)
. (5.31)
Тогда в худшем случае ошибка вычисленного значения интеграла на всем интервале интегрирования не будет превосходить сумму локальных погрешностей  , т.е. не будет превосходить заданного уровня погрешности.
, т.е. не будет превосходить заданного уровня погрешности.
|
|
|
Способ вычисления интеграла с автоматическим выбором шага имеет то преимущество, что он “приспосабливается” к особенностям подынтегральной функции: в областях резкого изменения функции шаг уменьшается, а там, где функция меняется слабо, – увеличивается. Такого рода алгоритмы называются адаптивными, т.е. приспосабливающимися. Использование адаптивных алгоритмов позволяет сократить затраты машинного времени без потери точности.
2) Управление вычислительным процессом.
Билет №10
1) Основные блоки для моделирования электрических систем.
2) Решение дифференциальных уравнений.
Билет №11
1) Решение дифференциальных уравнений.
2) Операции с комплексными числами.
Операции над комплексными числами
Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:
1. Коммутативность сложения: 
2. Ассоциативность сложения:
| (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3) |
3. Существует такое число z = 0, которое обладает свойством 
4. Для любых двух чисел z 1 и z 2 существует такое число z, что z 1 + z = z 2. Такое число z называется разностью двух комплексных чисел и обозначается z = z 2 – z 1.
5. Коммутативность умножения: 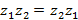
6. Ассоциативность умножения: 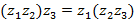
7. Дистрибутивность сложения относительно умножения:
| z 1(z 2 + z 3) = z 1 z 2 + z 1 z 3 |
8. Для любого комплексного числа z:
| z · 1 = z. |
9. Для любых двух чисел  и
и  существует такое число z, что
существует такое число z, что  . Такое число z называется частным двух комплексных чисел и обозначается
. Такое число z называется частным двух комплексных чисел и обозначается 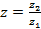 Деление на 0 невозможно.
Деление на 0 невозможно.
Билет №12
1) Определение модели.
модель – это объект-заместитель объекта-оригинала, обеспечивающий изучение определенных свойств оригинала.
2) Комплексные числа.
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей.
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.
Модулем комплексного числа называется длина вектора, соответствующего этому числу: 
Модуль комплексного числа z обычно обозначается 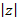 или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора
или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором  величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
|
|
|
Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
|
|
|


