Нахождение числовых характеристик выборки

Кафедра: «Высшая математика»

 

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

 

 

Тема: «Проверка гипотезы о законе распределения генеральной совокупности X по критерию Пирсона»

 

Выполнил:

 

 

Проверил:

 

 

Дата ___________

 

Оценка ___________

 

 

Омск-2011

 

Содержание

 

1. Исходные данные............................................... 3

2. Построение вариационного ряда.................................. 3

3. Построение интервального вариационного ряда..................... 4

4. Построение гистограммы........................................ 5

5. Нахождение числовых характеристик выборки...................... 6

6. Выдвижение гипотезы о законе распределения генеральной

совокупности Х................................................. 7

7. Оценка числовых характеристик и параметров закона распределения...7

8. Нахождение доверительного интервала для математического ожидания..7

9. Проверка гипотезы о законе распределения генеральной совокупности
по критерию Пирсона........................................... 8

 

Вариант № 2

Исходные данные

Дана выборка из генеральной совокупности случайной величины Х. Данные представлены в таблице 1.

Таблица 1

8,0	12,5	15,4	6,9	11,4	7,2	10,5	11,5
17,7	13,6	15,1	13,4	17,9	18,6	9,8	12,6
14,9	7,3	16,5	15,5	12,9	11,0	16,8	18,4
12,8	11,4	13,5	16,2	14,3	12,1	12,2	18,1
10,9	7,9	17,9	18,6	10,5	13,7	10,3	17,2
13,5	17,7	6,7	17,1	16,4	7,1	16,9	14,2
11,3	15,2	15,8	12,3	9,9	15,6	18,9	14,2
8,2	11,5	18,6	19,0

 

Выборка содержит 60 наблюдаемых значений, поэтому выборка имеет объем n = 60.

Построение вариационного ряда

Операция расположения значений случайной величины по не убыванию называется ранжированием. Последовательность элементов х⁽¹⁾ ≤ х⁽²⁾ ≤…≤ х^(k) называется вариационным рядом, элементы которого называют вариантами.

Проранжировав статистические данные, получаем вариационный ряд (таблица 2).

Таблица 2

№		№		№		№		№		№
	6,7		10,3		12,1		13,6		15,6		17,7
	6,9		10,5		12,2		13,7		15,8		17,9
	7,1		10,5		12,3		14,2		16,2		17,9
	7,2		10,9		12,5		14,2		16,4		18,1
	7,3				12,6		14,3		16,5		18,4
	7,9		11,3		12,8		14,9		16,8		18,6
			11,4		12,9		15,1		16,9		18,6
	8,2		11,4		13,4		15,2		17,1		18,6
	9,8		11,5		13,5		15,4		17,2		18,9
	9,9		11,5		13,5		15,5		17,7

Построение интервального вариационного ряда

Опытные данные объединяем в группы так, чтобы в каждой отдельной группе значения вариант будут одинаковы, и тогда можно определить число, показывающее, сколько раз встречается соответствующая варианта в определенной (соответствующей) группе.

Численность отдельной группы сгруппированного ряда опытных данных называется выборочной частотой соответствующей варианты x⁽ⁱ⁾ и обозначается n_i; при этом , где n – объем выборки.

Отношение выборочной частоты данной варианты к объему выборки называется относительной выборочной частотой P_i^*, т.е. 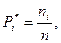где индекс i – номер варианты.

Т.к. согласно теореме Бернулли имеем, что т.е. выборочная относительная частота сходится по вероятности соответствующей вероятности, тогда из условия:

Интервальным вариационным рядом распределения называется упорядоченная совокупность частичных интервалов значений случайной величины с соответствующими им частотами или относительными частотами.

Для построения интервального вариационного ряда выполняем следующие действия:

1. Находим размах выборки R = x_max – x_min. Имеем R = 19 – 6,7 = 12,3.

2. Определяем длину частичного интервала ∆ – шаг разбиения по формуле Стерджеса: 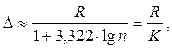где n – объем выборки, К – число частичных интервалов. Т.к. n =60, то , ∆ 2.

3. Определяем начало первого частичного интервала . Выбираем х_нач =5,7.

После разбиения на частичные интервалы просматриваем ранжированную выборку и определяем, сколько значений признака попало в каждый частичный интервал, включая в него те значения, которые ≥ нижней границы и меньше верхней границы. Строим интервальный вариационный ряд (табл. 3).

Таблица 3

 

 

Построение гистограммы

Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 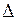, а высоты равны отношению – плотность частоты (или – плотность частости).

Для построения гистограммы строим вспомогательную таблицу 4.

Таблица 4

i	Разряды	ni
			0,0833	0,04165	6,7
			0,05	0,025	8,7
			0,2	0,1	10,7
			0,1833	0,09165	12,7
			0,1667	0,08335	14,7
			0,1334	0,0667	16,7
			0,1833	0,09165	18,7
Контроль		=60	=1

 

По данным таблицы 4 строим гистограмму частостей (рис. 1).

5,7 7,7 9,7 11,7 13,7 15,7 17,7 19,7 х

Рис. 1.

Гистограмма частостей является статистическим аналогом дифференциальной функции распределения (плотности) случайной величины Х. Площадь гистограммы частостей равна единице.

Нахождение числовых характеристик выборки

Рассчитаем статистическое среднее по формуле:

Вычислим статистическую дисперсию:

Вычислим среднее квадратическое отклонение:

.

Вычислим выборочный коэффициент асимметрии:

Вычислим выборочный коэффициент эксцесса:

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: