 |
Терминология. Краткое содержание. 8. Окно в бесконечность
|
|
|
|
Терминология
Квалиа — субъективные аспекты чувственного опыта.
Бихевиоризм — инструментализм применительно к психологии. Учение о том, что наука может (или должна) измерять и предсказывать лишь поведение людей в ответ на стимулы.
Краткое содержание
В области (универсального) искусственного интеллекта не достигнуто никакого прогресса из-за нерешённой философской проблемы, лежащей в её основе: мы не понимаем, как устроено творческое мышление. Как только мы разберёмся в этом, запрограммировать его не составить труда. Даже искусственной эволюции мы, возможно, ещё не добились, несмотря на видимость обратного. Проблема заключается в том, что мы не понимаем природу универсальности системы репликации ДНК.
8. Окно в бесконечность
Много столетий назад математики поняли, что с бесконечностями можно уверенно работать и извлекать из этой абстракции пользу. Бесконечные множества, бесконечно большие величины, а также бесконечно малые — всё имеет смысл. Многие их свойства трудны для понимания, появление теорий о бесконечных величинах всегда вызывало споры; но ведь и многие факты о конечных сущностях столь же контринтуитивны. То, что Докинз называет «аргументом, основанном на личном недоверии», — не аргумент: это всё равно что предпочитать парохиальные заблуждения универсальным истинам.
С античных времён над бесконечностью размышляли и в физике. Евклидово пространство было бесконечным; так или иначе, пространство обычно рассматривалось как континуум: даже конечный отрезок состоял из бесконечного множества точек. Между двумя произвольными моментами времени также было бесконечно много моментов. Но до изобретения Ньютоном и Лейбницем дифференциального исчисления, метода анализа непрерывных изменений в терминах бесконечного числа бесконечно малых изменений, представление о непрерывных величинах было обрывочно и противоречиво.
|
|
|
«Начала бесконечности» — возможность неограниченного роста знания в будущем — зависят от ряда других бесконечностей. Одна из них — универсальность законов природы, позволяющая применять конечные, локальные символы ко всему времени и пространству, а также ко всем известным и всем возможным явлениям. Другое понятие — существование физических объектов, являющихся универсальными объяснителями, — людей, — которые, как оказывается, обязательно являются и универсальными конструкторами, и должны содержать в себе универсальные классические компьютеры.
Многие формы универсальности сами по себе ссылаются на бесконечность некоторого вида, хотя их всегда можно трактовать как нечто неограниченное, а не актуально бесконечное. Противники бесконечности называют это «потенциальной бесконечностью», в отличие от «реализованной»[44]. Например, начало бесконечности можно описать либо как условие, при котором «прогресс в будущем будет неограничен », либо как условие, при котором «будет достигнут бесконечный по масштабу прогресс». Но я использую эти понятия взаимозаменяемо, потому что в данном контексте между ними нет содержательной разницы.
В философии математики существует направление, называемое финитизмом, в котором утверждается, что существуют только конечные абстрактные сущности. Так, например, натуральных чисел бесконечно много, но финитисты настаивают на том, что это просто фигура речи. По их словам, в действительности существует лишь конечное правило для образования каждого натурального числа (или, точнее говоря, его записи) из предыдущего, а ничего реально бесконечного тут нет. Но это учение сталкивается со следующей проблемой: есть ли в ряду натуральных чисел наибольшее? Если есть, то это противоречит существованию правила, позволяющего построить ещё большее число. Если нет, то неверно, что количество натуральных чисел конечно. И здесь финитистам приходится отрицать логический принцип, называемый «законом исключённого третьего», который гласит, что для каждого содержательного утверждения верно либо оно, либо его отрицание. Согласно финитистам получается, что, хотя среди натуральных чисел нет наибольшего, их всё равно не бесконечно много.
|
|
|
Финитизм — это инструментализм применительно к математике: это принципиальное неприятие объяснения. Он пытается рассматривать математические сущности только как процедуры, которым следуют математики, правила для написания значков на бумаге и так далее — и иногда это полезно, но связи с реальностью в этом нет, разве что с конечными объектами из опыта, такими как два яблока или три апельсина. Поэтому финитизм по сути своей антропоцентричен, что неудивительно, так как согласно ему ограниченность есть достоинство теории, а не наоборот. У финитизма есть и ещё один роковой недостаток, который привносят в науку инструментализм и эмпиризм: допущение, что у математиков есть своего рода привилегированный доступ к конечным сущностям, а к бесконечным — нет. Но это не так. Все наблюдения нагружены теорией. Любые абстрактные теоретические рассуждения — тоже. Добраться до абстрактных сущностей, конечных или бесконечных, как и до физических сущностей, можно только через теорию.
Другими словами, финитизм, как и инструментализм, — это не что иное, как план, цель которого помешать достижению прогресса в понимании сущностей, выходящих за рамки непосредственного опыта. А значит, и достижению прогресса вообще, ведь, как я объяснил, в рамках нашего «непосредственного опыта» сущностей нет.
Всё вышеприведённое обсуждение предполагает универсальность разума. Сфера досягаемости науки имеет неотъемлемые ограничения; это относится и к математике, и к любому направлению философии. Но если вы считаете, что существуют границы той области, в которой разум есть должный судья идей, значит, вы верите в иррациональное или в сверхъестественное. Аналогично, если вы отрицаете бесконечное, то вы застряли в конечном, а конечно парохиально. Здесь нельзя остановиться посередине. Самое разумное объяснение чего бы то ни было в конечном счёте включает в себя универсальность, а значит, и бесконечность. Сферу объяснимого нельзя взять и ограничить в приказном порядке.
|
|
|
Одним из проявлений этого в математике стал принцип, впервые явно сформулированный в девятнадцатом веке математиком Георгом Кантором, согласно которому абстрактные сущности можно определить любым желаемым способом через другие сущности при условии, что определения однозначны и непротиворечивы. Кантор заложил основы современного математического исследования бесконечности. В двадцатом веке его принцип отстаивал и обобщал математик Джон Конуэй, который дал ему эксцентричное, но вполне подходящее название — движение за освобождение математиков. Согласно Конуэю, открытия Кантора встретили резкое неприятие со стороны современников, включая большинство математиков того времени и также многих учёных, философов — и богословов. Как это ни парадоксально, религиозные возражения по сути строились на принципе заурядности. Попытки понять бесконечность и работать с ней в них характеризовались как посягательство на прерогативу Бога. В середине двадцатого века, через много лет после того, как исследования в области бесконечности стали обычным для математики делом и нашли в ней бесчисленное множество приложений, философ Людвиг Витгенштейн всё ещё презрительно осуждал их за «бессмысленность». (Правда, в конечном итоге он предъявил это обвинение и философии в целом, включая свою собственную работу, см. главу 12. )
Я уже упоминал другие примеры принципиального неприятия бесконечности. Необъяснимую антипатию к универсальным системам записи чисел выражали Архимед, Аполлоний и другие. Существуют такие учения, как инструментализм и финитизм. Принцип заурядности начинает с того, чтобы уйти от ограниченности взглядов и добраться до бесконечности, но в итоге загоняет науку в бесконечно малый, непредставительный пузырь постижимости. Есть ещё пессимизм, который (как будет показано в следующей главе) стремится объяснить неудачи существованием конечной границы совершенствования. Один из примеров пессимизма — парадоксальная парохиальность сравнения Земли со звездолётом — транспортным средством, которое гораздо лучше подошло бы в качестве метафоры бесконечности.
|
|
|
Всякий раз обращаясь к бесконечности, мы опираемся на бесконечную сферу применимости какой-либо идеи. Всегда, когда идея бесконечности имеет смысл, это связано с тем, что существует объяснение, каким образом некий конечный набор правил для манипулирования конечными символами ссылается на нечто бесконечное. (Повторю, что это также лежит в основе всех остальных наших знаний. )
В математике бесконечность изучается посредством бесконечных множеств (то есть множеств с бесконечным числом элементов). Определяющее свойство бесконечного множества заключается в том, что некоторая его часть содержит столько же элементов, сколько всё оно в целом. Возьмём, например, натуральные числа:

В верхней строке на рисунке каждое натуральное число встречается ровно один раз. В нижней строке содержится только часть этого множества: натуральные числа, начиная с 2. Чтобы показать, что в этих двух множествах одинаковое число элементов, на рисунке между ними установлено соответствие, которое математики называют «взаимно однозначным».
Чтобы проиллюстрировать некоторые интуитивные вещи, от которых приходится отказаться, рассуждая о бесконечности, математик Давид Гильберт придумал мысленный эксперимент. Он представил себе гостиницу с бесконечным числом номеров: отель «Бесконечность». Номера пронумерованы с помощью натуральных чисел, начиная с 1 и заканчивая… Чем же?
Число на двери последнего номера отеля — не бесконечность. Во-первых, последнего номера вообще нет. Мысль о том, что в любом пронумерованном множестве гостиничных номеров есть элемент с наибольшим числом на двери, — это первое интуитивное представление из повседневной жизни, которое придётся отбросить. Во-вторых, в любой конечной гостинице, в которой номера пронумерованы от 1, будет один под номером, равным общему их числу, а также другие с близкими номерами: если бы номеров было десять, на двери одного из них стояло бы десять, а среди остальных был бы номер девять. Но в отеле «Бесконечность», в котором число номеров бесконечно, порядковые номера их всех бесконечно далеки от бесконечности.
|
|
|

Теперь представьте, что отель заполнен. В каждом номере может жить один и только один человек. Когда «заполнена» конечная гостиница, это всё равно что «свободных мест нет». Но в отеле «Бесконечность» место найдётся всегда. Одно из условий пребывания в нём — постояльцам придётся сменить номер, когда администратор их об этом попросит. По прибытии нового гостя по системе оповещения проходит сообщение: «Просим всех постояльцев немедленно переехать в номер, на двери которого число на единицу больше, чем на двери занимаемого вами сейчас номера». Таким образом, по схеме, представленной на первом в этой главе рисунке, тот, кто жил в номере 1, переезжает в номер 2, а тот, кто жил в номере 2, — в номер 3 и так далее. Что же происходит в последнем номере? Но ведь последнего нет, и такого вопроса просто не возникает. Вновь прибывший заселяется в номер 1. Бронировать место в отеле «Бесконечность» не нужно.
Очевидно, в нашей Вселенной не может быть такого места, как отель «Бесконечность», поскольку в нём нарушается несколько законов физики. Однако это математический мысленный эксперимент, поэтому единственное ограничение на воображаемые законы физики — их непротиворечивость. И из-за этого требования непротиворечивости они контринтуитивны: в интуитивных вещах, касающихся бесконечности, часто отсутствует логика.
Переезжать таким образом немного неудобно, хотя все номера одинаковые, и их убирают перед заселением нового постояльца. Но людям нравится останавливаться в «Бесконечности». Дело в том, что отель недорогой, всего доллар за ночь, но при этом невероятно роскошный. Как это удаётся? Каждый день, собрав по доллару за комнату, администратор распределяет доход следующим образом. Деньги, полученные от жильцов из номеров 1–1000, идут на шампанское и клубнику для постояльцев, на оплату услуг горничных и остальные расходы, но только для номера 1. На деньги, полученные от жильцов из номеров 1001–2000, оплачивается всё то же самое для номера 2 и так далее. Таким образом, на каждый номер каждый день приходится товаров и услуг на сумму в несколько сотен долларов, но при этом удаётся получить и прибыль, и всё из расчёта одного доллара за сутки.
Слава отеля ширится, и однажды на местную станцию приезжает бесконечно длинный поезд с бесконечным числом пассажиров, которые хотели бы остановиться в отеле. На бесконечно много оповещений по системе громкой связи ушло бы слишком много времени (к тому же по гостиничным правилам каждого постояльца можно просить совершить то или иное действие лишь конечное число раз в день), но это не важно. Администратор просто сообщает: «Просим всех постояльцев немедленно переехать в номер с числом на двери в два раза больше, чем число на двери вашего нынешнего номера». Очевидно, что это не составит труда, и в итоге занятыми окажутся только чётные номера, а в нечётные можно будет заселять вновь прибывших. Этого как раз хватит, чтобы принять бесконечно много новых постояльцев, потому что нечётных чисел ровно столько же, сколько натуральных, что иллюстрируется следующим рисунком:

Таким образом, первый вновь прибывший селится в номер 1, второй — в номер 3 и так далее.
Затем в один прекрасный день на ту же станцию прибывает бесконечное число бесконечно длинных поездов, целиком забитых желающими остановиться в отеле. Но администраторов это не пугает. Они просто немного усложняют объявление, с которым читатели, разбирающиеся в математической терминологии, могут ознакомиться в сноске[45]. В итоге номеров хватает всем.
Однако переполнить отель «Бесконечность» математически возможно. В 1870-е годы Кантор сделал ряд замечательных открытий и среди прочего доказал, что не все бесконечности равны. В частности, бесконечность континуума — число точек на отрезке (которое равно числу точек во всём пространстве или в пространстве-времени) — гораздо больше, чем бесконечность натуральных чисел. Для доказательства этого факта Кантор продемонстрировал, что не существует взаимно однозначного соответствия между натуральными числами и точками отрезка: у этого множества точек порядок бесконечности выше, чем у множества натуральных чисел.
Вот один из вариантов его доказательства, основанное на так называемом диагональном методе. Представьте себе колоду карт: её толщина — один сантиметр, а карты такие тонкие, что на каждое «действительное число» сантиметров между 0 и 1 приходится по карте. Действительные числа можно определить как десятичные дроби, лежащие в этих пределах, например, 0, 7071…, где многоточие означает, что дальше знаков может быть бесконечно много. Тогда невозможно раздать эту колоду по одной карте в каждый номер отеля «Бесконечность». Предположим, что колоду всё же удалось распределить таким образом, и докажем, что это приводит к противоречию. Каждому номеру должна соответствовать карта, как, например, в таблице ниже. (Конкретные числа в ней не играют роли, поскольку мы доказываем, что действительные числа нельзя распределить по натуральным ни в каком порядке. )

Обратим внимание на бесконечную последовательность цифр, выделенных полужирным шрифтом — 6996 …. А теперь рассмотрим десятичное число, построенное следующим образом: оно начинается с нуля, затем идёт десятичная запятая, а затем произвольные цифры с тем лишь исключением, что каждая из них должна отличаться от соответствующей по номеру цифры в бесконечной последовательности 6996 …. Например, можно выбрать такое число: 0, 5885…. Карта с построенным таким образом номером не могла попасть ни в один номер в отеле, потому что первой цифрой она отличается от карты, отправленной в номер 1, второй — от карты, попавшей в номер 2, и так далее. Таким образом, она отличается от всех карт, присвоенных номерам в отеле, что противоречит исходному предположению о том, что распределены были все карты.
Бесконечность, размеры которой позволяют поставить её во взаимно однозначное соответствие с натуральными числами, называется счётной — термин достаточно неудачный, потому что в реальности досчитать до бесконечности никто не сможет. Но он подразумевает, что в принципе до каждого элемента счётного бесконечного множества можно дойти, если считать элементы в некотором подходящем порядке. Бесконечности большего размера называются несчётными. Таким образом, между любыми двумя отдельными точками содержится несчётное бесконечное множество действительных чисел. Более того, существует несчётное множество порядков бесконечности, каждый из которых слишком велик, чтобы его можно было поставить во взаимно однозначное соответствие с более низкими порядками.
Ещё одно важное несчётное множество — множество всех логически возможных перераспределений постояльцев по номерам в отеле «Бесконечность» (или, как говорят математики, множество всех возможных перестановок натуральных чисел). Это можно легко показать, если взять любое перераспределение, заданное бесконечно длинной таблицей, например, такой.
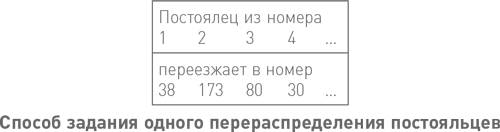
Теперь представим, что все возможные перераспределения идут списком друг под другом, так что мы можем подсчитать количество строк. Если применить к этому списку диагональный метод, то окажется, что такой список невозможен, а значит, множество всех возможных перераспределений несчётно.
Поскольку администраторам отеля «Бесконечность» приходится задавать перераспределение в виде публичного объявления, оно должно состоять из конечной последовательности слов, то есть конечной последовательности символов из какого-либо алфавита. Множество таких последовательностей счётно, поэтому оно бесконечно меньше, чем множество возможных перераспределений. А значит, задать можно только бесконечно малую часть всех логически возможных перераспределений. Это замечательное в своём роде ограничение очевидно неограниченных возможностей администраторов отеля «Бесконечность» по перетасовке постояльцев! Получается, что почти все способы, которыми на уровне логики можно было бы перераспределить людей по номерам, недоступны.
В отеле «Бесконечность» — уникальная, самодостаточная система сбора отходов и избавления от них. Каждый день постояльцев сначала перераспределяют так, чтобы все комнаты были заняты. Затем даётся следующее объявление: «Просим всех в течение следующей минуты собрать мусор в мешок и передать его жильцу из следующего по порядку номера. Если в течение этой минуты вы получите мешок, за следующие 30 секунд передайте его дальше. Если за эти 30 секунд вы получите мешок, передайте его дальше в течение следующих 15 секунд и так далее». Чтобы выполнить такую просьбу, постояльцам нужно делать всё быстро, но передавать мешки бесконечно быстро никому не придётся, как не придётся иметь дело и с бесконечно большим числом мешков. Каждый человек произведёт конечное число действий, как и предписывают правила отеля. Всякая передача мусора прекратится уже через две минуты. Таким образом, по истечении этого времени ни у кого из постояльцев мусора не останется.
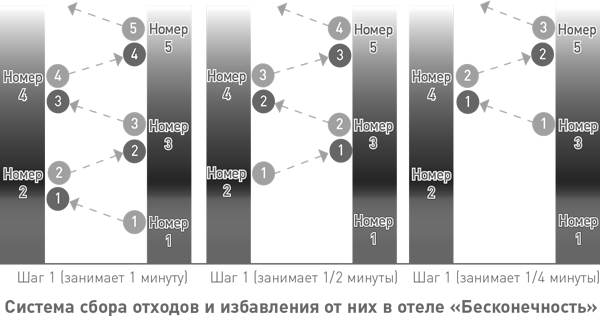
Весь собранный в отеле мусор из Вселенной исчезает. Исчезает в никуда. Но никто его в это «никуда» не транспортирует: каждый постоялец просто передаёт часть мусора в другой номер. Это «никуда», в которое исчез весь мусор, в физике называется сингулярностью. Сингулярности встречаются и в реальной жизни — в чёрных дырах и кое-где ещё. Но не будем отвлекаться: сейчас мы говорим о математике, а не о физике.
В отеле «Бесконечность», безусловно, бесконечно много персонала. Каждым постояльцем должны заниматься несколько служащих. Они приравниваются к постояльцам отеля, они также живут в пронумерованных комнатах и получают те же услуги, что и всякий другой постоялец, включая приписанных к ним служащих. В то же время они не могут просить этих служащих выполнять работу за себя, ведь, если все они сделают это, отель просто перестанет работать. В бесконечности нет ничего магического. В ней установлены логические правила: в этом и есть вся суть мысленного эксперимента с отелем «Бесконечность».
Порочная идея возможности переложить свою работу на других служащих из комнат с бó льшими номерами называется бесконечным регрессом. И это одна из тех вещей, которые на законных основаниях с бесконечностью делать нельзя. Есть старая шутка об одном любителе каверзных вопросов, который на лекции по астрофизике перебил лектора, чтобы настоять на том, что Земля плоская и стоит на слонах, которые в свою очередь стоят на огромной черепахе. «А на чём стоит черепаха? » — спросил его лектор. «На другой черепахе». — «А она на чём? » «Вы меня не проведёте, — торжествующе заявил слушатель. — Там и дальше стоят черепахи — друг на друге». Эта теория плохо объясняет явление, но не потому, что она не может объяснить всё (это не под силу ни одной теории), а потому, что необъяснённым остаётся по сути как раз то, что первоначально предполагалось объяснить. (Другим примером бесконечного регресса может служить теория о том, что того, кто задумал биосферу, тоже кто-то задумал, и так до бесконечности. )

Однажды в отеле «Бесконечность» в мешок с мусором залезает щенок одного из постояльцев. Хозяин этого не замечает и передаёт мешок с щенком в следующий номер.
Через две минуты щенок пропадает в никуда. Его хозяин в панике звонит администратору. Тот по системе оповещения объявляет: «Приносим свои извинения. В один из мешков с мусором случайно попал ценный предмет. Просим всех постояльцев проделать действия по удалению мусора в обратном порядке, как только вы получите мешок из номера, следующего по порядку за вашим».
Но всё бесполезно. Никто мешки не возвращает, потому что соседи из следующих по порядку номеров тоже ничего не возвращают. Мешки действительно уходят в никуда, это было не преувеличение. Их не складывали в вымышленном «номере бесконечность». Их больше нет, и щенка тоже нет. Никто ему ничего не сделал, его просто передавали из номера в номер. Но ни в одном номере его нет. Его нет нигде в отеле и вообще нигде. Если в конечной гостинице перемещать предмет из одного номера в другой в любой сложной последовательности, в итоге он окажется в каком-нибудь из них. Но когда номеров бесконечно много, это не так. Каждое отдельное действие каждого постояльца было безвредно для щенка и абсолютно обратимо. Но все они вместе привели к его исчезновению, и вернуть ничего уже нельзя.
Обращение действий не поможет, потому что — если бы оно сработало — нельзя было бы объяснить, почему в номер хозяина передали именно щенка, а не котёнка. Конечно, если щенок возвратился, это можно объяснить тем, что его передали из следующего по порядку номера и так далее. Но вся эта бесконечная последовательность объяснений никогда не сможет объяснить, «почему именно щенок»? Это ведь тоже бесконечный регресс.
А что если однажды щенок всё-таки окажется в номере 1, пройдя обратным путём через все номера? Это событие не является логически невозможным: этому просто не будет объяснения. В физике такое «нигде», откуда возвратился бы щенок, называется «голой сингулярностью». Голые сингулярности встречаются в некоторых спекулятивных теориях в физике, но эти теории заслуженно подвергаются критике за то, что не позволяют ничего предсказать. Как сказал однажды Хокинг, «из [голой сингулярности] могли бы появляться и телевизоры». Всё было бы иначе, будь у нас закон природы, определяющий то, что возникает, ведь в этом случае не было бы бесконечного регресса, а сингулярность не была бы «голой». Большой взрыв мог быть сингулярностью такого относительно благоприятного типа.
Я сказал, что номера в отеле идентичны, но на самом деле есть одно отличие: числа на их дверях. Таким образом, с учётом типов заданий, которые время от времени поступают от администраторов, более востребованы номера с небольшими числами. Например, у того, кто остановился в номере 1, есть уникальная привилегия: ему не приходится иметь дело с чужим мусором. Переехать в этот номер — всё равно что сорвать джекпот. Переехав в номер 2, чувствуешь себя уже немного не так, но тоже хорошо. Однако у каждого постояльца на двери номера написано число, необыкновенно близкое к началу. И каждый находится в более привилегированном положении, чем практически все остальные. Заезженное обещание политиков облагодетельствовать всех вполне осуществимо в отеле «Бесконечность».
Каждый номер в отеле стоит в начале бесконечности. И этим также характеризуется неограниченный рост знаний: мы всё ещё далеки от понимания всей сути, и так будет всегда.
Таким образом, в отеле «Бесконечность» нет такого понятия, как «типичный номер комнаты». Каждый из них нетипично близок к началу нумерации. Интуитивное представление о том, что в любом множестве значений должно быть «типичное» или «среднее», для бесконечных множеств неверно. То же самое относится и к тому, что мы интуитивно считаем «редким» и «часто встречающимся». Можно заметить, например, что половина натуральных чисел — нечётна, а половина — чётна и что среди натуральных чисел чётные и нечётные таким образом встречаются одинаково часто. Но рассмотрим следующую перестановку:

Теперь кажется, что нечётные числа встречаются в два раза реже, чем чётные. Аналогичным образом можно было бы показать, что нечётные числа выпадают один раз на миллион или в любой другой пропорции. Таким образом, и интуитивное понятие доли элементов к бесконечным множествам неприменимо.
После ужасного исчезновения щенка администрация отеля «Бесконечность» решает приятно удивить своих постояльцев, чтобы они больше не переживали по этому поводу. Объявляется, что каждый получит в подарок книгу «Начало бесконечности» или мою предыдущую книгу «Структура реальности». Книги раздаются следующим образом: в каждый миллионный номер отправляется более старая книга, а более новая — во все остальные.
Предположим, вы остановились в этом отеле. И вот вам доставляют книгу, обёрнутую в непрозрачную подарочную бумагу. Вы надеетесь получить новую, потому что предыдущую уже прочитали. И вы вполне уверены, что так и будет, ведь шансы, что ваш номер — один из тех, в которые отправят старую книгу, невелики? Ровно один на миллион, как вам кажется.
И только вы собираетесь разорвать упаковку, как раздаётся объявление. Всем нужно перейти в другой номер согласно числу, указанному на карточке, которая появится вслед за книгой из специального жёлоба в стене. В объявлении также говорится, что при новом размещении все, кто получил одну конкретную книгу, попадут в нечётные номера, а те, кто получил другую, — в чётные, но не уточняется, кто в какие. И по числу на двери своего нового номера вы не можете сказать, какая книга досталась вам. Безусловно, проблем с таким переселением не возникает, ведь обе книги получило бесконечно много людей.
Приходит карточка, и вы переезжаете в другой номер. Стала ли меньше ваша уверенность относительно того, какая у вас книга? Надо полагать, нет. Если рассуждать, как раньше, сейчас ваши шансы получить «Начало бесконечности» — один из двух, потому что теперь она есть в «половине номеров». Поскольку вы пришли к противоречию, то, по-видимому, вероятность вы оценивали неправильным методом. На самом деле неправильны все методы оценки такой вероятности, потому что, как показывает этот пример, в отеле «Бесконечность» нет такого понятия, как вероятность того, что вы получили одну книгу, а не другую.
С точки зрения математики в этом нет ничего исключительного. Этот пример лишь снова демонстрирует, что такие признаки, как вероятный и невероятный, редкий или часто встречающийся, типичный или нетипичный не имеют буквально никакого значения, когда речь идёт о сравнении бесконечных множеств натуральных чисел.
Но если обратиться к физике, то это плохие новости для антропных доводов. Представьте себе бесконечное множество вселенных с одними и теми же законами физики, кроме того, что одна конкретная физическая постоянная, обозначим её D, принимает в каждой из них разное значение. (Строго говоря, нам следует представить себе несчётное бесконечное множество вселенных, по аналогии с бесконечно тонкими картами, но это только усугубит проблему, которую я собираюсь описать, так что не будем усложнять. ) Предположим, что из этих вселенных у бесконечно большого числа значения D таковы, что астрофизики в них появляются, и у бесконечно большого числа значения D таковы, что они не появляются. Тогда пронумеруем вселенные так, что все те, в которых есть астрофизики, будут чётными, а те, в которых их нет, — нечётными.
Это не означает, что в половине вселенных астрофизики есть. Как и при распределении книг в отеле «Бесконечность», мы могли бы с тем же успехом пометить вселенные так, что астрофизики были бы только в каждой третьей или триллионной, или в каждой триллионной их бы не было. Таким образом, с антропным объяснением проблемы тонкой настройки что-то не так: мы можем избавиться от неё, если мы просто перенумеруем вселенные. По своему желанию мы можем пронумеровать их так, что наличие астрофизиков будет казаться правилом, исключением или чем-то промежуточным.
Теперь предположим, что мы с помощью соответствующих законов физики с разными значениями D вычисляем, появятся ли астрофизики. Оказывается, что для значений D вне диапазона от, скажем, 137 до 138, вселенных с астрофизиками очень мало, по одной на триллион. А внутри этого диапазона только в одной вселенной на триллион астрофизиков нет, а при значениях D от 137, 4 до 137, 6 они есть во всех. Хочу подчеркнуть, что в реальной жизни мы и близко не подошли к хорошему пониманию процесса формирования астрофизиков, чтобы вычислять такие значения, и вероятно, никогда его не поймём, как станет ясно из следующей главы. Но независимо от того, можем мы их вычислять или нет, теоретики, придерживающиеся антропного объяснения, предпочтут проинтерпретировать эти числа так: если мы измерим значения D, то вряд ли они окажутся вне диапазона от 137 до 138. Но в действительности ничего подобного они не означают! Ведь мы можем просто изменить нумерацию вселенных (перетасовать бесконечную колоду «карт»), и частоты встречаемости поменяются с точностью до наоборот или станут такими, как нам будет угодно.
Научные объяснения, вероятно, не могут зависеть от выбранного нами способа пометки сущностей, на которые ссылается теория. Поэтому антропная аргументация сама по себе не может ничего предсказать. И по этой причине, как я говорил в главе 4, она не может объяснить тонкую настройку физических констант.
Остроумный вариант антропного принципа был предложен физиком Ли Смолином[46]. Он опирается на то, что согласно некоторым теориям квантовой гравитации чёрная дыра может породить внутри себя целую новую вселенную. Смолин предполагает, что в этих новых вселенных могут быть другие законы физики и что, более того, на эти законы будут влиять условия, существующие в порождающей вселенной. В частности, разумные существа в порождающей вселенной могут сделать так, что чёрные дыры будут порождать вселенные с удобными для индивидуальных существ законами физики. Но в объяснениях такого типа (известных как «эволюционные космологии») есть одна загвоздка: а сколько вселенных было вначале? Если их было бесконечно много, то непонятно, как их подсчитывать, а из-за того, что каждая вселенная с астрофизиками породит несколько других, доля таких вселенных не увеличится заметным образом. Если не было первой или первых вселенных и весь этот ансамбль существует уже бесконечное время, то теория сталкивается с проблемой бесконечного регресса. Ведь тогда, как заметил космолог Франк Типлер[47], вся совокупность должна была «бесконечно давно» прийти в равновесное состояние, а это означало бы, что эволюции, приведшей к этому равновесию, — того самого процесса, который должен объяснить тонкую настройку, никогда не было (как щенок, который пропал в никуда ). Если же изначально была только одна вселенная или конечное их число, то остаётся проблема тонкой настройки в исходной вселенной (вселенных): были ли в них астрофизики? Надо полагать, не было; но если бы исходные вселенные порождали бы огромную цепь вселенных-потомков, пока в одной из них, чисто случайно, не появились бы астрофизики, это всё равно не дало бы ответа на вопрос, почему вся система, функционирующая теперь согласно одному закону физики, в котором кажущиеся «константы» изменяются по законам природы, допускает этот в конечном счёте благоприятствующий появлению астрофизиков механизм. И такому совпадению не будет антропного объяснения.
Теория Смолина имеет рациональное зерно: она предлагает всеохватывающую систему для множества вселенных и некоторые физические связи между ними. Но объяснение связывает только «дочерние» вселенные и «порождающие» их, а этого недостаточно. Поэтому всё это не работает.
Но теперь предположим, что мы также рассказываем о реальности, которая соединяет все эти вселенные и наделяет предпочтительным физическим смыслом один из способов их маркировки. Например, так. Девочка по имени Лира, которая родилась во вселенной № 1, изобретает прибор, с помощью которого можно перемещаться в другие вселенные. Прибор также создаёт вокруг девочки маленькую защитную сферу, обеспечивающую её жизнь в тех вселенных, где по законам физики жизнь не возможна. Удерживая определённую кнопку, Лира перемещается из одной вселенной в другую, в фиксированном порядке, с интервалом ровно в одну минуту. Как только она отпускает кнопку, то сразу попадает домой, в свою вселенную. Обозначим вселенные числами 1, 2, 3 и так далее в порядке их посещения.
Иногда Лира берёт с собой устройство для измерения константы D и ещё одно, чтобы, как в проекте поиска инопланетян SETI, только быстрее и надёжнее, вычислять, есть ли во вселенной астрофизики. Лира надеется проверить предсказания антропного принципа.
Она может посетить только конечное число вселенных, и у неё нет возможности судить о том, являются ли они репрезентативной выборкой из всего бесконечного множества. Но у устройства есть второй режим. При нём прибор переносит Лиру во вселенную № 2 за минуту, затем во вселенную № 3 за полминуты, во вселенную № 4 за четверть минуты и так далее. Если она не отпустит кнопку к моменту истечения двух минут, то посетит все вселенные в бесконечном множестве, то есть в рамках этого повествования все существующие. После этого прибор автоматически возвращает Лиру во вселенную № 1. Если она снова нажмёт кнопку, то путешествие начнётся снова со вселенной № 2.
Большая часть вселенных мелькает перед глазами Лиры так быстро, что она их даже не замечает. Но измерительные устройства, которые она взяла с собой, не подвержены ограничениям, свойственным человеческим органам чувств, и не подчиняются нашим законам физики. Если их включить, они покажут скользящее среднее значений из всех посещённых вселенных, независимо от того, сколько времени они находились в каждой из них. Так, например, если в чётных вселенных ас
|
|
|


