 |
Монотонная, если она не содержит отрицаний переменных.
|
|
|
|
Перевод чисел из двоичной системы счисления в восьмеричную.
Решаем показательное уравнение:
2=2i i=1
8 = 2i. Так как 8 = 23, то i = 3 бита.
Каждый разряд восьмеричного числа содержит 3 бита информации.
Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 1010012 в восьмеричное:
101 0012 => 1 × 22 + 0 × 21 + 1 × 20 0 × 22 + 0 × 21 + 1 × 20 => 518.
Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры:
| Двоичные триады | ||||||||
| Восьмеричные цифры |
Восьмеричная в двоичную
Пусть требуется перевести восьмеричное число 24738 в двоичное число. Воспользовавшись Таблицей соответствия из Приложения, получим:
24738 = 101001110112,
3) Число с фиксированной запятой — формат представления вещественного числа в памяти ЭВМ в виде целого числа. При этом само число x и его целочисленное представление x′ связаны формулой
,
где z — цена (вес) младшего разряда.
Простейший пример арифметики с фиксированной запятой — перевод рублей в копейки. В таком случае, чтобы запомнить сумму 12 рублей 34 копейки, мы записываем в ячейку памяти число 1234.
Числа с плавающей запятой
4)Прямой обратный код
Арифметические операции в двоичной системе счисления
Сложение
Сложение одноразрядных двоичных чисел выполняется по следующим правилам:
|
|
|
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10
Сложим для примера два любых двоичных числа:
+101
------
Вычитание
Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
0 - 0 = 0
1 - 0 = 1
0 - 1 = (заем из старшего разряда) 1
1 - 1 = 0
Пример:
- 101
----
Умножение
Умножение одноразрядных двоичных чисел выполняется по следующим правилам:
0 * 0 = 0
1 * 0 = 0
0 * 1 = 0
1 * 1 = 1
Логическая функция
Бу́лева фу́нкция (или логи́ческая функция, от n переменных — в дискретной математике отображение Bn → B, где B = {0,1} — булево множество. Элементы булева множества 1 и 0 обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементыдекартова произведения
Bn называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается P 2, а от n переменных — P 2(n).Названия булевых функций от одной переменной:
| Обозначение | Название |
| тождественный ноль, тождественная ложь, тождественное "НЕТ" | |
| x̅, x, x' | отрицание, логическое "НЕТ", "НЕ", "НИ", "NOT"(англ.), "NO"(англ.) |
| x | тождественная функция, логическое "ДА", "YES"(англ.) |
| тождественная единица, тождественная истина, тождественное "ДА", |
Дизъюнктивная нормальная форма (ДНФ)
Простой конъюнкцией называется конъюнкция некоторого конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Элементарная конъюнкция
§ правильная, если в неё каждая переменная входит не более одного раза (включая отрицание);
§ полная, если в неё каждая переменная (или её отрицание) входит ровно 1 раз;
|
|
|
монотонная, если она не содержит отрицаний переменных.
Например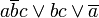 
— является ДНФ.
[ править ] Конъюнктивная нормальная форма (КНФ)
Конъюнктивная нормальная форма1 (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.
КНФ может быть преобразована к эквивалентной ей ДНФ путём раскрытия скобок по правилу:
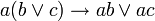
Точно также можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило
7) Отрицание, НЕ
Инвертор, НЕ
| A | − A |
Мнемоническое правило для отрицания звучит так: На выходе будет:
§ «1» тогда и только тогда, когда на входе «0»,
§ «0» тогда и только тогда, когда на входе «1»
§ 
§ Через Uвх1 и Uвых1 обозначены уровни входного и выходного напряжений, соответствующие логической единице, а через Uвх0 и Uвых0 — соответствующие логическому нулю. Различают время задержки tзр10 распространения при переключении из состояния 1 в состояние 0 и при переключении из состояния 0 в состояние 1 — tзр01, а также среднее время задержки распространения tзр, причем 
Время задержки принято определять по перепадам уровней 0,5D Uвх и 0,5D Uвых. Максимальная рабочая частота Fмакс — это частота, при которой сохраняется работоспособность схемы.
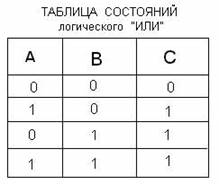
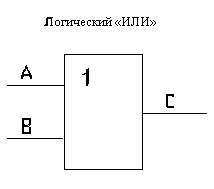
. Это модель логического сложения. На выходе появляется сигнал “1” только в том случае, когда есть сигнал или на входе А, или на входе В, или на том и другом одновременно будет 0
8)Логический элемент “ИЛИ”
сложение
на схемах изображается в виде прямоугольника. Внутри прямоугольника ставится “1”.
Элемент «И» (AND)
Умноение
Вот так выглядит элемент «И» и его таблица истинности:
:
|
|
|
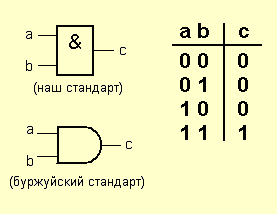
