 |
Обратная матрица. Ранг матрицы.
|
|
|
|
Обратная матрица
Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
А·А-1=А-1·А=Е.
Для существования матрицы А -1необходимым и достаточным условием является требование | А |¹0.
Если определитель матрицы отличен от нуля (| А |¹0), то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при | А |=0) — вырожденной, или особенной.
Задание 1. Укажите, какие из матриц имеют обратные, а также выделите невырожденные (неособенные) и вырожденные (особенные) матрицы:
 вывод: $!
невырожденные матрицы (неособенные):
вырожденные матрицы (особенные):
вывод: $!
невырожденные матрицы (неособенные):
вырожденные матрицы (особенные):
|
 вывод: $!
невырожденные матрицы (неособенные):
вырожденные матрицы (особенные):
вывод: $!
невырожденные матрицы (неособенные):
вырожденные матрицы (особенные):
|
Теорема (необходимое и достаточное условие, существования обратной матрицы). Обратная матрица А -1 существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Обратную матрицу можно найти с помощью элементарных преобразований:
по следующему алгоритму:
1. выпишем заданную квадратную матрицу А и припишем ей справа соответственную единичную матрицу Е;
2. с помощью элементарных преобразований получим слева вместо матрицы А единичную Е:
¨ получим значение первого диагонального элемента а 11=1, при этом можно строки менять местами (полностью), умножать на любое, отличное от нуля число, и складывать поэлементно;
¨ получим значения аi 1=0,  , где i ¹1, то есть добьёмся, чтобы все остальные элементы первого столбца стали равными нулю;
, где i ¹1, то есть добьёмся, чтобы все остальные элементы первого столбца стали равными нулю;
¨ далее аналогично, получим значение второго диагонального элемента а 22=1, и добьёмся, чтобы все остальные элементы второго столбца стали равными нулю аi 2=0,  , где i ¹2;
, где i ¹2;
|
|
|
¨ далее аналогично, будем получать значение диагонального элемента равное 1, и всех остальных элементов этого столбца равными нулю
3. тогда при соответствующих элементарных преобразованиях матрица Е превратится в А -1.
| А / Е ~ Е / А -1 |
Задание 2. Найти обратную матрицу с помощью присоединенной единичной и элементарных преобразований и выполнить проверку правильности её нахождения:


 , следовательно, обратная матрица существует. , следовательно, обратная матрица существует.
 Проверка:
А·А-1=А-1·А=Е
Проверка:
А·А-1=А-1·А=Е

|
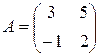
 , следовательно, обратная матрица существует. , следовательно, обратная матрица существует.
 Проверка:
А·А-1=А-1·А=Е
Проверка:
А·А-1=А-1·А=Е

|

|
Задание 3. Найти обратную матрицу с помощью присоединённой единичной и элементарных преобразований и выполнить проверку правильности её нахождения:



 , следовательно, обратная матрица существует. , следовательно, обратная матрица существует.
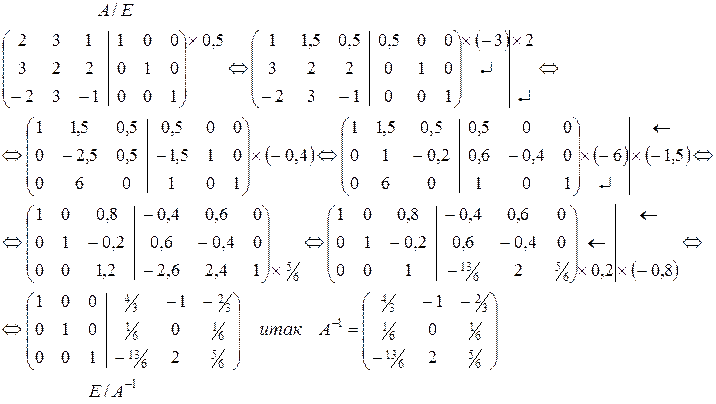 Проверка: А·А-1=А-1·А=Е
Проверка: А·А-1=А-1·А=Е

|

 следовательно, обратная матрица существует.
следовательно, обратная матрица существует.
 Проверка:
А·А-1=А-1·А=Е
Проверка:
А·А-1=А-1·А=Е

|

|
Обратную матрицу можно найти с помощью определителя и алгебраических дополнений:
например, для матрицы второго порядка А ищем А -1 – обратную матрицу (если она существует) по формуле:

Задание 4. Найти обратную матрицу с помощью определителя и алгебраических дополнений:

 Þ$! А -1. Þ$! А -1.
 получили, что
получили, что
 Итак,
Итак,

| 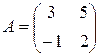
 Þ$! А -1. Þ$! А -1.
 получили, что
получили, что
 Итак,
Итак,

|

 Þ$! А -1. Þ$! А -1.
 получили, что
получили, что
 Итак,
Итак,

| 
 Þ$! А -1. Þ$! А -1.
 получили, что
получили, что
 Итак,
Итак,

|
например, для матрицы третьего порядка А ищем А -1 – обратную матрицу (если она существует) по формуле:

Задание 5. Найти обратную матрицу с помощью определителя и алгебраических дополнений:




| 



|




| 


|
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обозначается rangА, или r (А).
Из определения следует:
1) ранг матрицы Ат,п не превосходит меньшего из её размеров, т.е. r (A)£ min (m; п);
|
|
|
2) r (A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А = О;
3) для квадратной матрицы п-го порядка r (A) =п тогда и только тогда, когда матрица А — невырожденная.
4) Укажите ранг матрицы:
| Пример матрицы | Ранг матрицы | Пример матрицы | Ранг матрицы | Пример матрицы | Ранг матрицы |

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 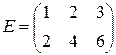
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
|
5) Выразите неизвестную матрицу из матричного уравнения:
| А · Х = В – умножим слева обе части на А -1; А -1· А · Х = А -1· В – где А -1· А = Е; Е · Х = А -1· В – где Е · Х = Х; Х = А -1· В | Y · A = В – умножим _______ обе части на __; Y = |
| А -1· Х · B = C | C -1· A · Y = C |
| Х · А · B = E | А · Х · A = E |
6) Решить матричное уравнение:

¨ Введём следующие обозначения: 
Тогда матричное уравнение примет вид: А · Х · В = С – умножим слева обе части матричного уравнения на А -1 – обратную матрицу для А и получим:
А -1· А · Х · В = А -1· С – заметим, что А -1· А = Е – единичная матрица и получим:
Е · Х · В = А -1· С – заметим, что Е · Х = Х и получим:
Х · В = А -1· С – умножим справа обе части матричного уравнения на В -1 – обратную матрицу для В и получим:
Х ·В· В -1= А -1· С · В -1 – заметим, что В · В -1= Е – единичная матрица и получим:
Х · Е = А -1· С · В -1 – заметим, что Х · Е = Х и получим:
Х = А -1· С · В -1
¨ Ищем обратную матрицу А -1 для А по формуле: 


Итак, обратная матрица имеет вид: 
¨ Ищем обратную матрицу В -1 для В по формуле: 

 Итак, обратная матрица имеет вид:
Итак, обратная матрица имеет вид: 
¨ Ищем матрицу Х:

Обратная матрица. Ранг матрицы.
Тест 1
| Вопрос 1Укажите невырожденную матрицу: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 2Укажите вырожденную матрицу: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 3Укажите верное утверждение: | ||||||
| а.) Всякая вырожденная матрица имеет обратную | б.) Всякая невырожденная матрица имеет обратную | в.) Всякая квадратная матрица имеет обратную | г.) Некоторые прямоугольные матрицы имеют обратные | |||
| Вопрос 4Укажите неверное утверждение: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 5Укажите верное утверждение: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 6Укажите верное утверждение: Если матрица А не квадратная, то может существовать такая матрица В, что: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 7Укажите верное утверждение: | ||||||
| а.) Если | A |=0, то | A -1|=0 | б.) Если | A |=2, то | A -1|=-2 | в.) Если | A |=2, то | A -1|=0,5 | г.) | A |·| A -1|=1 | |||
| Вопрос 8Укажите матрицы, для которых ранг равен 1: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 9Укажите матрицы, для которых ранг равен 2: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 10Укажите матрицы, для которых ранг равен 3: | ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
| Вопрос 11Укажите неверное утверждение: | ||||||
| а.) при транспонировании матрицы её ранг не меняется | б.) при вычёркивании нулевой строки (столбца) матрицы её ранг не меняется | в.) при элементарных преобразованиях матрицы её ранг не меняется | г.) при вычёркивании ненулевой строки (столбца) матрицы её ранг не меняется | |||
| Вопрос 12Укажите верное утверждение: | ||||||
| а.) ранг матрицы может быть равен 0 | б.) ранг матрицы может быть меньше 0 | в.) ранг матрицы может быть равен 2,5 | г.) ранг матрицы может быть равен 10 | |||
| Вопрос 13Укажите верное утверждение: Если ранг матрицы A равен r, то | ||||||
| а.) r (2A)=2 r | б.) r (2A)=0,5 r | в.) r (2A)= r 2 | г.) r (2A)= r | |||
| Вопрос 14Укажите верное утверждение: Если ранг матрицы A равен r, то | ||||||
| а.) r (-A)=- r | б.) r (-A)= r | в.) r (0·A)= r | г.) r (0·A)=1 | |||
Вопрос 15Решить матричное уравнение: 
| ||||||
а.) 
| б.) 
| в.) 
| г.) Æ | |||
Вопрос 16Решить матричное уравнение: 
| ||||||
а.) 
| б.) 
| в.) 
| г.) Æ | |||
Вопрос 17Решить матричное уравнение: 
| ||||||
а.) 
| б.) 
| в.) 
| г.) Æ | |||
Вопрос 18Решить матричное уравнение: 
| ||||||
а.) 
| б.) 
| в.) 
| г.) Æ | |||
Вопрос 19Решить матричное уравнение: 
| ||||||
а.) 
| б.) 
| в.) 
| г.) Æ | |||
Вопрос 20Найти А · А -1, где 
| ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
Вопрос 21Найти обратную матрицу для 
| ||||||
а.) 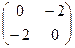
| б.) 
| в.) 
| г.) 
| |||
Вопрос 22Найти обратную матрицу для 
| ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
Вопрос 23Найти обратную матрицу для 
| ||||||
а.) 
| б.) 
| в.) 
| г.) 
| |||
Вопрос 24Найти обратную матрицу для 
| ||||||
а.) 
| б.) 
| в.) 
| г.) не существует | |||
|
|
|
|
|
|


