 |
Метод наименьших квадратов
|
|
|
|
Математическая обработка результатов экспериментальных данных
Метод наименьших квадратов ~ Регрессионный анализ ~ Экстраполяция
Изучая теорию интерполяции, вы познакомились с интерполяционными формулами, которые в точности воспроизводят значения данной функции в узлах интерполяции. Однако в ряде случаев выполнение этого условия затруднительно или даже нецелесообразно:
1. Если заданные величины х и у являются экспериментальными данными, то могут содержать в себе существенные ошибки, т.к. получены в результате измерений или наблюдений. Поэтому построение аппроксимирующего многочлена, воспроизводящего в точности заданное значение функции, означало бы тщательное копирование допущенных при измерениях ошибок.
2. Если имеются точные значения функции в некоторых точках, но число таких точек n весьма велико, то интерполяционный многочлен будет очень высокой степени (если только разности не будут становиться постоянными).
Поэтому возникает задача построения многочлена некоторой вполне определенной степени, но меньшей чем n - 1, который хотя и не дает точных значений функции в узлах интерполяции, но достаточно близко к ним подходит.
Метод наименьших квадратов
Метод наименьших квадратов (МНК) состоит в следующем: для данных значений x = х 0, х 1 ,..., хn и y = y 0, y 1 ,..., yn подобрать многочлен заданной степени m<n вида
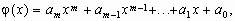
| (1) |
- непрерывная функция для аппроксимации F(xi)=yi принимающий в заданных точках хi значения как можно более близкие к табличным значениям yi.
В узлах функции F(xi) и φ(xi) будут отличаться на величину
εi= F(xi) - φ(xi)
Отклонения εi могут принимать положительные и отрицательные значения. Чтобы не учитывать знак, возведем каждое отклонение в квадрат и просуммируем.
|
|
|
Метод построения аппроксимирующей функции φ(х) исходя из условий минимума величины Q называется методом наименьших квадратов (МНК).
Наиболее распространенный способ выбора функции φ(х) – в виде линейной комбинации.
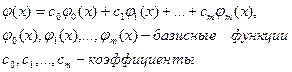
m≤n
коэффициенты, определяемые из условия минимизации величины Q.
Математически условие минимума суммы квадратов отклонения Q запишем, приравнивая частные производные от Q по коэффициентам СК, где 0≤к≤m.
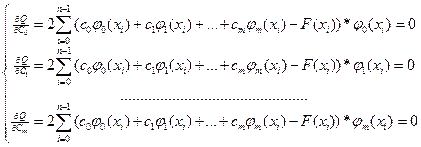
Из данной системы СЛАУ определяются все коэффициенты ск. Система называется системой нормальных уравнений. Матрица данной системы имеет вид:
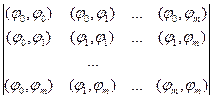
И называется матрицей Грамма. Элементы матрицы Грамма являются скалярными произведениями базисных функций
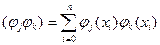
Расширенная матрица системы уравнений получится добавлением справа к матрице Грамма столбца свободных членов
Где скалярные произведения, являющиеся элементами столбца, определяются аналогично
Отметим основные свойства матрицы Грамма, полезные при программной реализации алгоритма МНК:
1) матрица симметрична, т.е. аi,j = aj,i, что позволяет сократить количество вычислений при заполнении матрицы;
2) матрица является положительно определенной;
3) определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции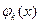 
, при этом система (4.3) имеет единственное решение.
При обработке экспериментальных данных, определенных с погрешностью ε в каждой узловой точке, обычно начинают с аппроксимации функции φ(х), представимой одной-двумя базисными функциями. После определения коэффициента ск вычисляют величину Q по формуле (4.1). Если получится, что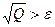 
, то необходимо расширить базис добавлением новых функций 
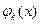. Расширение базиса необходимо осуществлять до тех пор, пока не выполнится условие 
.
Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции f(x), таких, как периодичность, экспоненциальный или логарифмический характер, свойства симметрии и т.д.
|
|
|
Степенной базис.
Выберем базисные функции 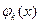в виде последовательности степеней аргумента х, которые линейно независимы,
.
В этом случае так же, как и при интерполяции, мы будем аппроксимировать экспериментальную зависимость полиномом. Однако степень полинома m выбираем обычно m «n. Аппроксимирующая кривая в МНК не проходит через значения исходной функции в узлах, но проведена из условия наименьшего суммарного квадратичного отклонения. Экспериментальные данные «сглаживаются» с помощью функции φ(х). Если выбрать m=n, то на основании единственности интерполяционного полинома получим функцию φ(х), совпадающую с каноническим интерполяционным полиномом степени n, аппроксимирующая кривая пройдет через все экспериментальные точки и величина Q=0. Последнее условие используется для отладки и тестирования программ, реализующих алгоритм МНК.
|
|
|
